Day 30, MAT115

Last Time

Next Time

Announcements:
- My office hour Zoom for tomorrow (usually 2pm) will move to 9:00am because of a meeting.
- This session will be captured on Zoom, if I remember to turn it on, and record it.
  Our page of zooms and the play-by-plays.
- You have a symmetry assignment (which is now due Monday, 4/11 -- revised).
- Our second exam is this Friday, 4/8. It will cover the following:
  - Planar graphs and Euler's formula
  - Euler Paths and Circuits
  - Mayan numbers
  - Babylonian numbers
  - Egyptian multiplication and division
  - Fibonacci numbers and spirals (from the Euclidean algorithm for finding the greatest common divisor)
  - Fibonacci Nim
  - Golden Rectangles and Spirals
  - All readings. Just as before, I'll be asking some short answer questions, just to check if you've been doing the readings.
    1. This reading on number systems
    2. Chapter 10: Working Your Quads;
    3. A short description of the Fibonacci numbers
    4. Is Geometry a Language That Only Humans Know? (here's the source -- the New York Times). Neuroscientists are exploring whether shapes like squares (regular rectangles) and and our ability to recognize them are part of what makes our species special.
  There won't be any questions about symmetry or the Platonic solids.
- We'll be reviewing today.

Last time:

Symmetric objects in three-dimensions: Platonic solids, which possess a great deal of symmetry: they're super-symmetric solids.

These are the analogs of the regular polygons

But, in contrast to the regular polygons (of which there are infinitely many), there are only five!

The Five Convex Regular Polyhedra (Platonic solids) -- thanks Wikipedia!
Tetrahedron	Hexahedron or Cube	Octahedron	Icosahedron	Dodecahedron
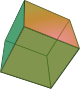
(Animation)	(Animation)	(Animation)	(Animation)	(Animation)
fire	earth	air	water	universe

We learned that they have twins -- duals -- that share certain properties.

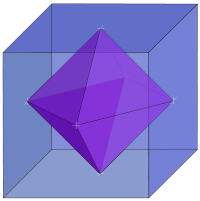
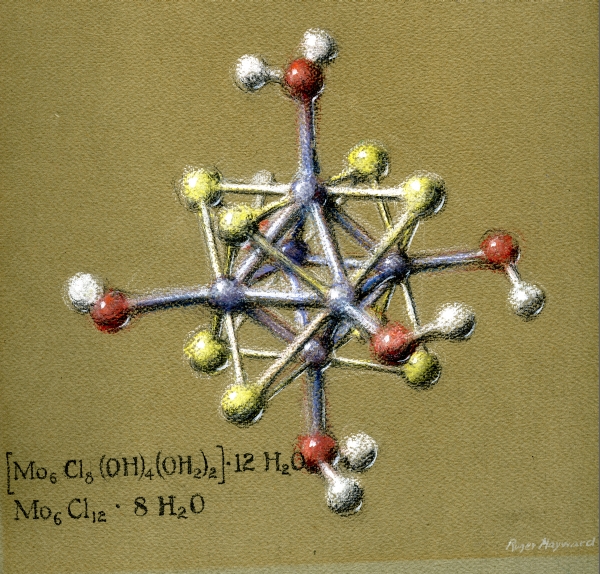
But one of the coolest things is that they fit within each other like "Russian dolls". And nature knows it, as shown in the compound of Molybdenum Dichloride molecules shown here.

Today's Question of the Day:

Are you ready for exam 2?
- I'll let you start with any questions you have.
- We'll start with a handout of Mayan and Babylonian number system examples. These problems just involve
  - Understanding the bases (20 and 60)
  - Understanding the quirks (360, rather than $20^2$; no zero)
  - Being able to translate between their systems and ours
- Egyptian multiplication isn't bad: let's just quickly remind ourselves of that with an example.
- I know that Egyptian division is among your greatest concerns. As I've said, I'll throw you only softballs! You need to know, however, that the Egyptians only liked unit fractions.
  I'll provide you with a unit fraction table sufficient to do any divisions that way (although you're also welcome to use the multiplication table, backwards).
  You may not have noticed a link that's been floating along at the bottom of many recent agendas: An amazing source for Egyptian Fraction info
  It includes an Egyptian fraction calculator (which is one of the reasons I didn't want to publicize it too much:)!
  You might also note that Fibonacci's name appears: in fact, he's the one who created the algorithm for the Egyptian calculator, in the same book in which he introduced "the rabbit problem" (which led to "his" numbers) -- the Liber Abaci -- published in 1202.
  A couple of examples:
  1. $\frac{27}{8}$
  2. $\frac{28}{13}$ (Unit Fraction Table)
- You'll have to play me in "Fraudini Nim":
  - Suppose we start with 43 counters: do you go first? What do you take?
  - Suppose we start with 34 counters: do you go first? What do you take?
  - Suppose we start with 18 counters: do you go first? What do you take?
- An "Euler room" problem is easy for me to concoct. Here's a problem that that Euler considered:
  
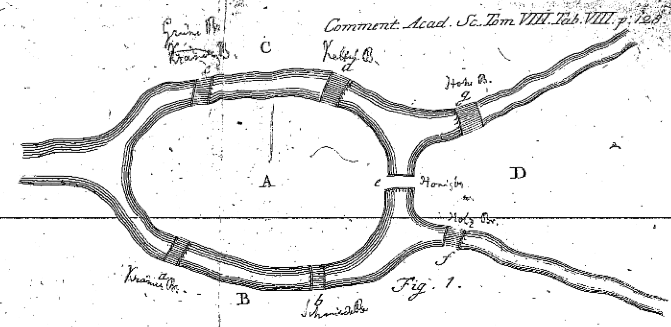
  It's easy for me to construct a similar example!
  - There's always only an even number of odd degree vertices (hand-shaking theorem)
  - If there are only 2, then there's an Euler path (and you have to start at one odd, and end at the other)
  - If there are zero odds, then there's an Euler circuit (start and end at the same node).
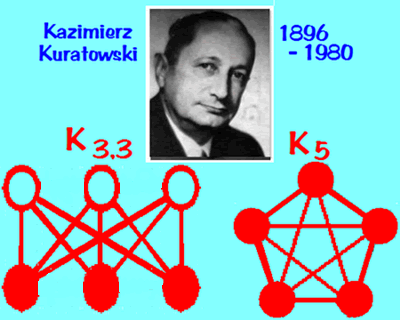
- Planar graphs are graphs which can be drawn on the page without "false intersections", and Kuratowski's theorem says that any non-planar graph has a copy of one of these two graphs in it somewhere, as a subgraph:
  
  Planar graphs satisfy Euler's formula, which I like to write as "ran 2": \[ r - a + n = 2 \] Regions minus arcs + nodes = 2.
  We'll see that this formula works for the Platonic solids, too!
Links:
- Symmetry, by Hermann Weyl (Princeton University Press, 1952)
- Symmetry of lifeforms on Earth
- A fun reading on symmetry
- Fibonacci Spiral Fractal maker.
- How to win at Nim
- Unit Fraction Table
- How Egyptians wrote fractions.
- Problem 81: converting between different measures with fractions
- Egyptian fractions (Wikipedia)
- An amazing source for Egyptian Fraction info
- The new Mayan glyphs from Xultun, Guatemala: lots of spectacular calendar calculations, but nothing whatsoever about 2012 AD
- "Ancient Maya Astronomical Tables from Xultun, Guatemala". William A. Saturno, David Stuart, Anthony F. Aveni, Franco Rossi
- Part of the wall from which our Mayan tablet is taken

Website maintained by Andy Long. Comments appreciated.


But one of the coolest things is that they fit within each other like "Russian dolls".	And nature knows it, as shown in the compound of Molybdenum Dichloride molecules shown here.