Day 38, MAT115

• This session will be captured on Zoom, if I remember to turn it on, and record it.

  Our page of zooms and the play-by-plays.

• You have an IMath assignment on the go, covering symmetry, and Platonic solids, and fractals (due Wednesday, 4/27 -- revised). More on that in a moment.

• A reminder that your logo projects are due next Monday. Be ready to present!

  I added that as an explicit assignment on Canvas. Those are due Monday, 5/2 -- and some of you will be presenting that day. So get your logo (the image, if you have one) to me by 11 am, at the latest -- so I can get them ready to show.

  If your logo is a song, or an interpretative dance, just be ready!:)

  The rest of the folks will present on Wednesday, 5/4. I will randomly choose those who are to present on that Monday! Very exciting; perhaps nerve-wracking. You all need to be here on Monday.

  If you are not here on Monday, then you have been pre-selected to present on Monday -- i.e., your logo will receive a zero.

  The Duke Energy logo is a Hopf link (if the bands weren't cut...:)

  

• Finally I graded your symmetry homework last week. Here's a key.

  Let's talk about that a bit.

• was rubber bands, as we made ourselves a set of Borromean rings.

• We got to know the essential cast of characters:
  • Links:
    1. The unlink (two circles lying on top of each other. Zero-crossing toroidal knot!)
    2. The Hopf link (two-crossing toroidal link)
    3. Solomon's Knot (four-crossing toroidal link)
    4. Borromean rings

  • Knots:
    1. The unknot (a circle; a one-crossing toroidal knot!) )
    2. The trefoil knot (three-crossing twist knot; three twist toroidal knot)
    3. The figure eight knot (four-crossing twist knot)
    4. The cinquefoil (five-crossing toroidal knot)
    5. The five-crossing twist knot

• We found out that many of our objects could be created as toroidal objects -- the edges of twisted bands.

  These are the torus knots, and several of our links.

  But others couldn't be (the figure-eight knot, the 5-crossing twist knot, the Borromean rings)

Before we get to that, however, two things:

1. Fractal practice!

   Fractals demonstrate exponential growth and decay. The length in this fractal is increasing exponentially, by a factor of $\frac{4}{3}$:

   

   The number of sticks is also growing exponentially, but by a factor of 4: each time, there are 4 times as many sticks!

   Let's do just a couple more examples.

   • a stick fractal
   • an area fractal

2. Then I want to introduce you to the RCO -- Really Cool Object -- which brings together the Borromean rings, golden rectangles, and Platonic solids (an icosahedron).

   This is the most beautiful piece of mathematics I know of:

   It turns out that there are golden rectangles in the heart of an icosahedron, interlocked as Borromean rings!

   

   We'll make some using 3x5 cards (which are not quite golden). Their corners are the 12 vertices of the icosahedron. The tricky part is locking them together!

• There are two different ways to think about making the trefoil knot: as a
  1. torus knot, and as a
  2. twist knot.
  Let's draw it in these two different ways.

• The figure-eight knot has four crossings, as does Solomon's "knot", but it's a link, not a knot. This is the first (interesting) instance of a knot and link with the same (minimal) number of crossings.

• We know that there are two distinct 5-crossing knots:
• To help you, we have the Rolfsen Knot Table
• The cinquefoil knot
• The five-crosssing twist knot is actually known (somewhat confusingly) as the 3-twist knot
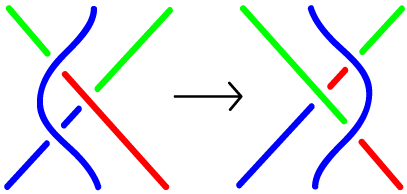
• How can we tell them apart? Are they really different? For that we need to study knot equivalence, and our primary tool, the Reidemeister moves.

How do we show that two knot projections ("squiggles") are the same knot ("knot equivalence")? That's the job of the Reidemeister moves.

1. What are the Reidemeister moves?
   • Tools for showing that two projections (pictures) of knots really show the same knot.
   • Names of the moves reflect the number of strands involved. A Strand is a piece of a knot picture that goes from undercrossing to undercrossing, with only overcrossings inbetween.
   • Reidemeister moves preserve the knot -- they don't change the knot. We're not cutting -- we're just going to shove parts of the knot around.

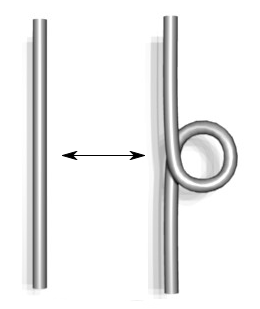
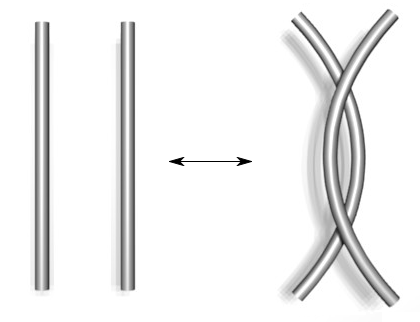
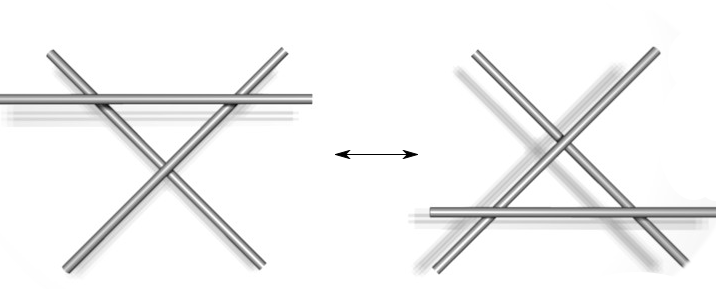
   • Type I	Type II	Type III

2. Using the Reidemeister moves
   1. to turn a projection of an unknot into another more complicated appearing unknot:

      We'll just try a few with a string, to see what we can learn.

   2. Now let's use these three moves to create equivalent versions of the trefoil knot, but using each of the three Reidemeister moves.

   3. A figure-eight knot is equivalent to its mirror reflection (a trefoil knot is not equivalent to its mirror!)

   4. Turning a more complicated appearing unknot into a simple circle unknot. (Here it is as a powerpoint presentation.)

3. Reidemeister moves and Tricolorability
   1. Tricolorability: "A knot is tricolorable if each strand of the knot diagram can be colored one of three colors, subject to the following rules:
      1. At least two colors must be used,
      2. at most three colors are used, and
      3. at each crossing, the three incident strands are either all the same color or all different colors.

   2. Tricolorability is preserved by Reidemeister moves:

      Reidemeister Move I is tricolorable.	Reidemeister Move II is tricolorable.	Reidemeister Move III is tricolorable.

   3. Therefore, if the projection of one knot is tricolorable and the other isn't, they're different knots (because we can't get from one to the other via Reidemeister moves).

   4. Theorem: there are at least two different knots.
      1. The unknot is not tricolorable ("At least two colors must be used");
      2. The trefoil knot is tricolorable:
      3. The figure-eight knot is not tricolorable (it requires four colors):
      4. Danger: many knots are tricolorable -- being tricolorable doesn't mean that your knot is the trefoil knot -- but it does mean that your knot is not the unknot!

         Links can be tricolorable, too -- for example, the unlink is tricolorable! (That's just two circles, one lying on top of the other, as in Borromean rings.)