-
- This session will be captured on Zoom, if I remember to turn it on, and record it.
- Our page of zooms and the play-by-plays.
- A reminder that your logo projects are
due this coming Monday. Be ready to present!
You all need to be here on Monday.
If you are not here on Monday, then you have been pre-selected to present on Monday -- i.e., your logo will receive a zero.
Here are some galleries of logos from years past. (How would you appraise them? Would you agree that they fall on a pretty broad spectrum?)
Over the weekend I was in Cincinnati, and I went dumpster-diving for this one (saw it on a dumpster): do you see the cinquefoil knot?

- I'll be posting some review material Monday and Wednesday next
week, to help get you ready for your final exam.
Remember you may make the Really Cool Object as a cheat link for the final. Make it out of 4x6 cards (it must be constructed to use it).
Then on Friday we'll review.
- You have a couple of reading assignments (one for today):
- Read Chapter 30: The Hilbert Hotel (for next class!)
- Check out this summary of our work today: Knots: a handout for math circles.
I made a digital rendition of Jancarlo's method of transitioning between the circle and that thing that looked like a four knot (but was truly an unknot).
- My mom got a present from my nephew yesterday -- he'd carved her
an owl. But I noticed what she was wearing around her neck, and
thought that you'd be interested:

(Is it Mobius?)
- Last night I got the most recent Science magazine, so I went
looking, as usual:
- I sure enjoyed looking over my new gallery of spirals!
Thanks for the fun. Dogs, cats, ducks, fish (fish fish!),
assorted other critters -- and galaxies, and knots, and... --
are especially appreciated. Thank you, thank you!
Some of these are pure art.
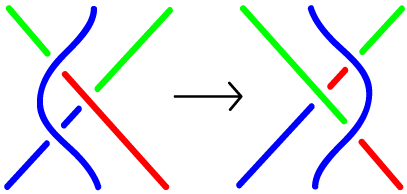
- How do we show that two knot projections ("squiggles") are the
same knot ("knot
equivalence")? That's the job of the Reidemeister
moves.
- What are the Reidemeister moves?
- Tools for showing that two projections (pictures) of knots really show the same knot.
- Names of the moves reflect the number of strands involved. A Strand is a piece of a knot picture that goes from undercrossing to undercrossing, with only overcrossings inbetween.
- Reidemeister moves preserve the knot -- they don't change the knot. We're not cutting -- we're just going to shove parts of the knot around.
-
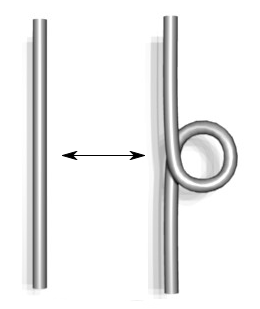
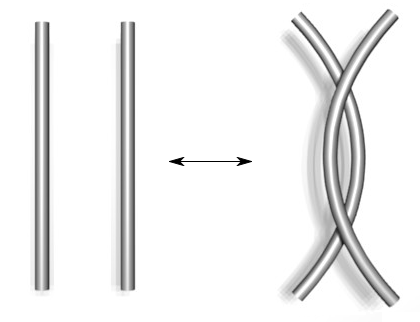
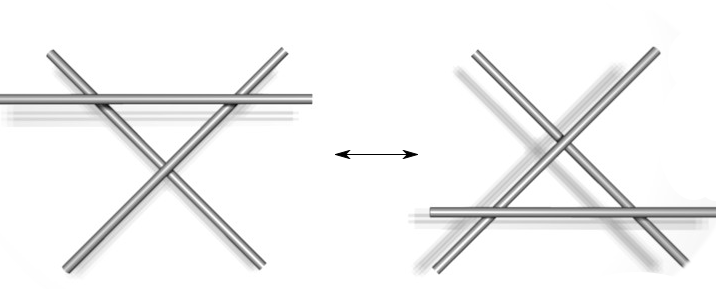
Type I Type II Type III
- Reidemeister moves and Tricolorability
- Tricolorability:
"A knot is tricolorable if each strand of the
knot diagram can be colored one of three
colors, subject to the following rules:
- At least two colors must be used,
- at most three colors are used, and
- at each crossing, the three incident strands are either all the same color or all different colors.
- Tricolorability is preserved by Reidemeister moves:
Reidemeister Move I is tricolorable. Reidemeister Move II is tricolorable. Reidemeister Move III is tricolorable. - Therefore, if the projection of one knot is
tricolorable and the other isn't, they're different
knots (because we can't get from one to the other via
Reidemeister moves).
- Theorem: there are at least two different knots.
- The unknot is not tricolorable ("At least two colors must be used");
- The trefoil knot is tricolorable:

- The figure-eight knot is not tricolorable (it requires four colors):

- Danger: many knots are tricolorable --
being tricolorable doesn't mean that your knot
is the trefoil knot -- but it does mean that
your knot is not the unknot!
Links can be tricolorable, too -- for example, the unlink is tricolorable! (That's just two circles, one lying on top of the other, as in Borromean rings.)
- Tricolorability:
"A knot is tricolorable if each strand of the
knot diagram can be colored one of three
colors, subject to the following rules:
- But, if you are claiming that a knot picture is a picture
of a trefoil knot, then the picture should be
tricolorable (because the trefoil is).
You might try to tricolor your knots (or links) for your knotty assignment. It's one more piece of information.
- What are the Reidemeister moves?
- Today: we end on a big note: Infinity....
Question of the day: shall anyone expel us from the paradise that Cantor has created? (Hilbert said "No!")
At Hilbert's Hotel, "it's always booked solid, but there's always a vacancy." That may sound strange, but infinity is strange -- so it's perfectly okay.
We want to focus on a strange fact about infinity: that when you get to sets that are infinitely sized, you find that their subsets can be exactly the same size as they are. This is very strange, and doesn't work with finite sets. So it's a very mysterious property.
It may depend on our understanding of what "size" means.
We'll illustrate with something called "The Hilbert Hotel" (Strogatz likes that name; I usually call it "Motel $\infty$" -- but I can see why Strogatz would like to honor Hilbert: he supported Cantor when he was proposing and trying to defend these "big ideas").
Here's the upshot of what Cantor discovered:
-
- First of all, mathematical fact one:
- Let's call the set of all of a set's subsets its power set. Pascal's triangle (that rascal!) shows you how many of each type of subset you have (for finite sets).

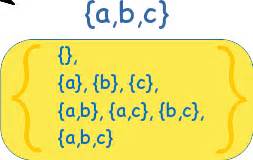
- Mathematical fact two:
- The power set of a set of $n$ elements contains $2^n$
elements.
(We know that since each row of Pascal's triangle adds to a power of 2.)
- Even the set containing no elements has one subset -- the set
itself. So the power set has one element -- has size bigger
than the set itself.
This property holds true for all finite sets -- and it turns out to be true for infinite sets, too!
- This means that, although the natural numbers $1,2,3,\ldots$ is
infinite as a set, there's a bigger set (the power set of the
natural numbers). Upshot: infinity comes in various sizes!
Infinitely many, in fact. Crazy sounding, I know -- but it's
true.
That symbol that you've been familiar with for all your lives, $\infty$: you thought it stood for a single thing; but it stands for a whole collection of monstrously big things, all too big to really think about properly. (Well, Cantor did!:)
- That's too crazy, it seems; but, nonetheless, mathematicians
know that it's true, because we can prove it! The key to
determining if two sets have the same size is the one-to-one
correspondence -- and that will be key for infinite sets, as
well.
- So we now begin considering "The Hilbert Hotel". The Hilbert Hotel
has natural numbered hotel rooms -- there's an infinite number
of rooms, labelled 1, 2, 3, 4, .... for every natural number.
- The place is packed, and one person shows up;
This result informs us that when someone on the playground hollers "I hate you infinity plus 1!", they really haven't hated any more than a simple infinity.
Alternatively, if your lover says they love you infinitely much, you can't impress them by saying that you love them infinitely plus one. They will scoff, and perhaps leave you for a better mathematician! So take note....

- The place is packed, and an infinite school bus shows up.
This result informs us that when someone on the playground hollers "I hate you 2*infinity!", they really haven't hated any more than a simple infinity.
- The place is packed, and an infinite number of infinite
school buses show up! (Buses numbered 1, 2, .... with
seats labelled 1, 2, ....)
This result proves that there are just as many rational numbers (ratios of integers) as there are integers.
The irrational numbers -- now there's an infinite set! It's too big for the hotel...:( Finally the Hilbert Hotel meets its match.
- So, in the end, here's what you say on the playground,
when you want to love your friend more:
"I love you more than the power set of your set of infinite love."
Amen!
- The place is packed, and one person shows up;
-
- Links
- Generate some of our favorite fractals on-line (you can even make some of your own!).
- Lindenmayer Systems: making fractals
- a Mathematical overview of recycling symbol style
Website maintained by Andy Long. Comments appreciated.