Day 28, Mat128: Calculus A

• If you need to Zoom to class, here's the link. Old Zooms are here.

• Your exams are due today. Please submit those with your originals attached. I'll have them back to you by Wednesday.

• Today we'll do two more examples:
  1. one from section 3.5 (related rates), and
  2. one from section 3.4 (optimization).
  Then I want to show you how we use tangent lines to find roots of functions (e.g. zeros of derivative functions).

• On Wednesday we'll do a review of the course.

We worked on section 3.5: related rates (section 3.5).

• These are in the same vein as the optimization problems: story problems, but with a twist -- as one might imagine, we're relating the rates of change (derivatives) of several different variables to each other.

• In calculus you are destined to encounter the famous ladder problem (in our textbook, you'll find it here). We wish to establish the rate of one thing, relative to the rate of the other. These are so-called "related rates". So the ladder's top rung is falling vertically at one speed, as the feet are slipping out at another. Speeds are, in this case, rates of change of positions.

• Related rates problems frequently involve implicit differentiation. One assumes that a pair of variables, which are related in an equation are varying in response to some associated independent variable (frequently time).

• In Stewart's calculus, he suggested this more detailed approach to related rates problems:
  1. Read the problem carefully.
  2. Draw a diagram if possible.
  3. Introduce (good) notation. Use sensible variable names. Assign symbols to all quantities that are functions of time (usually time will be our independent variable).
  4. Express the given information and the required rate in terms of derivatives.
  5. Write an equation that relates the various quantities of the problem. If necessary, use the geometry of the situation to eliminate one of the variables by substitution.
  6. Use the Chain Rule to differentiate both sides of the equation with respect to t.
  7. Substitute the given information into the resulting equation and solve for the unknown rate.
  8. Don't forget your units.

  Warning: a common error is to substitute the given numerical information (for quantities that vary with time) too early. Substitute only after the differentiation is complete.

• Let's look at two examples from the text:
  1. Activity 3.5.4 from section 3.5 (related rates)
     

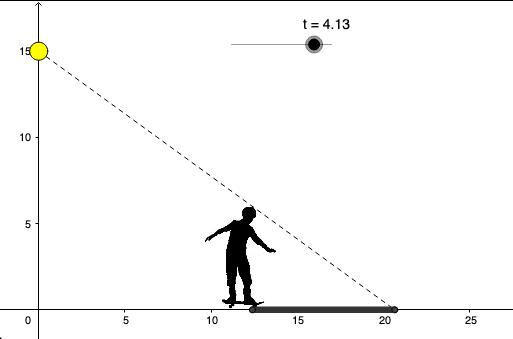
  2. Exercise 8 from section 3.4 (optimization).

• Then I want to show you how we use tangent lines to find roots of functions (e.g. zeros of derivative functions), via a Mathematica demonstration of Newton's method

• If there's any time left, we'll take a look at your worksheet for 3.5.

  You should solve each, thinking along these lines:

  1. UPCE: Understand, Plan, Carry out, Evaluate
  2. Draw pictures
  3. Give meaningful names (letters) for variables.
  4. Establish reasonable domains for variables
  5. Establish a reasonable coordinate system
  6. Doodle relationships!
  7. Establish a relationship between the variables whose rates will be related.
  8. Compute derivatives, usually implicitly, which are now also related.
  9. Solve for the rate of interest (frequently given at a particular point in time).

• A Chain Rule tutorial
• Our free, on-line textbook, called Active Calculus.