Day 17, Mat128: Calculus A

The method exploits (even bad) guesses and tangent lines, whose roots are easy to find, to construct a succession of iterates which may converge to the root of interest.

Once again we see the importance of linear things -- and persistence!

• One thing we noticed is that tangent and cotangent, and secant and cosecant are very similar (and hence their derivatives are very similar).

  It's the periodicity of the sine and cosine functions that make it so: as noted last time, while it is true that \[ \sin'(x) = \cos(x) \] one can also see that \[ \sin'(x) = \sin\left(x+\frac{\pi}{2}\right) \]

  This is a trig identity ($\cos(x)=\sin\left(x+\frac{\pi}{2}\right)$ -- so we don't even really need two functions -- one is just a shift of the other); but it says something really interesting: differentiation is like a shift operator for sine.

  Sine looks down the road by $\frac{\pi}{2}$ for the slope of the tangent line at a point:

• Similarly, we can transform a sine into cosine, via \[ \sin(x) = \cos\left(x-\frac{\pi}{2}\right) \]
• From this we can see, however, that \[ \sin(-x) = \cos\left(-x-\frac{\pi}{2}\right) \] and, since sine is an odd function and cosine an even function, \[ \sin(-x) = -\sin(x) = \cos\left(-(x+\frac{\pi}{2})\right) = \cos\left(x+\frac{\pi}{2}\right) \] We put these together, to get \[ \cot(x) = \frac{\cos(x)}{\sin(x)} = \frac{\sin\left(x+\frac{\pi}{2}\right)}{-\cos\left(x+\frac{\pi}{2}\right)} = -\tan\left(x+\frac{\pi}{2}\right) \]

• These are examples of compositions of functions: the computation of cosine can be accomplished by first an affine transformation -- \(x+\frac{\pi}{2}\) -- followed by an application of sine. If we define \[ g(x)=x+\frac{\pi}{2} \] and \[ f(x)=\sin(x) \] then we can define cosine as \[ \cos(x)=f(g(x)) \] I like to talk about "x going on a voyage", passing first by \(g\) and then, transformed by the experience, undergoing transformation by \(f\) -- finally becoming \(\cos(x)\). A metamorphosis!

We will first derive the chain rule, then see how to make use of it.

Let's look at a few more of the compositions involved there: the chain rule is about differentiating function compositions, and the steps involve

• identification (of the functions making up the composition)
• knowing the derivatives of the component functions

• The chain rule is so critically important because of the importance of compositions of functions:

  Theorem (the chain rule): If $F(x) = f(g(x))$, and both $f$ and $g$ are differentiable at $x$, then \[ F^\prime(x) = f^\prime(g(x))g^\prime(x) \]

  I personally think about the chain rule this way:

  "f prime of stuff times the derivative of the stuff"; or

  "f prime of stuff times stuff prime.",

  where $f$ is the "outside" function (so $g$ is the "stuff"):

  \[ F^\prime(x) = f^\prime(stuff)stuff^\prime \]

  You can see that the rule is fairly simple, once you've identified the composition -- that is, once you've torn apart $F$ to find $f$ and $g$.

  You might take a look at this summary from my pre-calc class to review compositions.

• The chain rule looks a little different in Leibniz notation, but you may see it written this way, too: if we let $y=F(x)=f(u)$, where $u=g(x)$, then \[ F'(x)=\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx} \] This alternative version of the formula helps us to remember that $x$ is going on a journey, passing first through $g$ to become something new ($u=g(x)$), and then continues on as $u$ through the function $f$ to become $y=f(u)$. It's a metamorphosis. It should be called the "metamorphosis rule", if there were any justice in the world....

• The difficulty is often identifying the composition. We'll try some easy ones first, then get to some ugly ones.

  Before we do that, however, I'd like to motivate (rather than prove) the chain rule, using the limit definition of the derivative. Everything comes from that!

  Basically, however, it relies on the tangent line: we want to use the fact that \[ g(x+h) \approx g(x) + hg'(x) \] Why does that make sense? Because it comes straight out of the limit definition, where we throw away the limit. That's why we have to write "$\approx"$:

  \[ g'(x) \approx \frac{g(x+h)-g(x)}{h} \]

• Examples (from Stewart's calculus): tearing apart functions
  • $F(x)=\sqrt{1-2x}$
  • $F(x)=6\cot(nx)$
  • $F(x)=4 + 0.35 \sin(2 \pi t / 5.4)$
  • Trickier: $F(x)=\sin(\sqrt{1 + x^2})$

• A sample problem involving compositions: model the seasonal variation in Keeling's CO2 data:
  

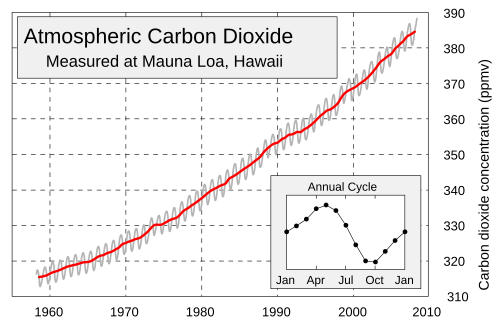
  If time were measured in years from January, would

  $V(t)=A\sin(2\pi{t})$

  be a good model? What would be a good choice for the parameter $A$?

• We do have a worksheet, but I doubt that we'll have any time in class to work on it! Give it a go before class on Monday.