Day 23, Mat128: Calculus A

"Fish all have osmolyte, a fluid in their cells that they use to counteract pressure -- it's the thing that makes that fishy smell," Jamieson said. "One of the only things, when you look at fish from a biochemical point of view, that is linear with depth is the concentration of that fluid." [ael: my emphasis]

"When you get to about 8,200 to 8,400 metres -- the variation is probably temperature-dependent ... it reaches what's called isosmosis, which means you can't increase the concentration of that fluid in the cells anymore." (ael: this means that it wasn't really linear with depth!)

Suppose $h(x)=\frac{f(x)}{g(x)}$, where $f$ and $g$ are differentiable and $g'(x) \ne 0$ near $a$ (except possibly at $a$). Suppose that \[ \lim_{x \to a}f(x)=0 \;\;{\text{and}}\;\; \lim_{x \to a}g(x)=0 \] Then \[ \lim_{x \to a}h(x)= \lim_{x \to a}\frac{f(x)}{g(x)} = \frac{f'(a)}{g'(a)} \] if the derivatives on the right side exists, and $g'(a) \ne 0$.

Now let's see how to derive this (or to make sense of it, at any rate): since $f(a)=g(a)=0$, we can write \[ \lim_{x \to a}h(x) = \lim_{x \to a}\frac{f(x)}{g(x)} = \lim_{x \to a}\frac{f(x)-f(a)}{g(x)-g(a)} = \lim_{x \to a}\frac{\frac{f(x)-f(a)}{x-a}}{\frac{g(x)-g(a)}{x-a}} = \frac{\lim_{x \to a}\frac{f(x)-f(a)}{x-a}}{\lim_{x \to a}\frac{g(x)-g(a)}{x-a}} = \frac{f'(a)}{g'(a)} \]

Examples:

• Activity 2.8.2. Evaluate each of the following limits. If you use L'Hôpital's rule, indicate where it was used, and be certain its hypotheses are met before you apply it:
  1. $\displaystyle \lim_{x \to 0} \frac{\ln(1 + x)}{x}$

  2. $\displaystyle \lim_{x \to \pi} \frac{\cos(x)}{x}$

  3. $\displaystyle \lim_{x \to 1} \frac{2 \ln(x)}{1-e^{x-1}}$

  4. $\displaystyle \lim_{x \to 0} \frac{\sin(x) - x}{\cos(2x)-1}$

• Last time we just glanced at the first page of your Section 2.8 worksheet: let's all take a look at those together.
  1. Important Note: the worksheet presents a slightly more general form of L'Hôpital's rule: because of how we derived the rule (using the limit definition), we arrived at \[ \lim_{x \to a}\frac{f(x)}{g(x)} = \frac{f'(a)}{g'(a)} \] However, more generally, we have that \[ \lim_{x \to a}\frac{f(x)}{g(x)} = \lim_{x \to a}\frac{f'(x)}{g'(x)} \] This is especially useful when we look at limits as \(x \to \pm \infty\) -- that is, for horizontal asymptotes.

  2. There are indeterminate forms which are not quotients, which can be turned into quotients in clever ways; and then one can apply L'Hôpital's rule.

• Today we talk a little more the extrema -- that is, maxima and minima -- places where a function takes on extreme values. One of the most important roles of the derivative is to identify those places where a function hits its maximum or minimum.
  • This frequently goes by the name of "optimization" -- we're trying to find the best way to do something, and setting a particular parameter at a certain value yields the best result. Our job is to find that particular value.... and the derivative is frequently our tool of choice.

    If you've ever fiddled with the dial on a radio, trying to get a station to come in better, you understand: you're adjusting the position of a value along an axis to get the clearest signal -- the maximal amount of signal to noise.

    It's the same with a thermostat, perhaps -- only you're fighting someone else in the house. For your money, you'd like it a little warmer; but they'd like it a little cooler. (This is a more complicated optimization problem!)

  • For this simpler type of optimization, we need this

    Definition 3.1.6.:

    We say that a function $f$ has a critical number (or critical point) at $x=c$ provided that $c$ is in the domain of $f$, and $f'(c)=0$ or $f'(c)$ is undefined.

• Finding and Characterizing Extrema:
  1. We are planning to build a rectangular pen for our dog. We only have 200 meters of fencing. What are the dimensions of the pen that will provide our dog the most area to play in?

     The area of the pen is $Area=width*length$, or $A=w*l$ -- but the two dimensions are not independent, since we know the perimeter: \[ 2(w+l)=200 \]

     Hence we conclude that \[ w+l=100 \] or that \[ l=100-w \]

     Therefore \[ A(w)=w*(100-w) \]

     Where is this function a maximum? Well, we don't even need calculus to solve this one -- we can use symmetry, and the fact that $A$'s graph is a parabola:

     The peak has to occur exactly half way between the roots (0 and 100), so when $w=50$. But this makes $l=50$ as well, indicating that the maximum area $A$ occurs when the pen is square, 50 meters by 50 meters (with an area of 2500$m^2$).

     But if we'd differentiated, sure enough we'd find that $w=50$ is the critical point: \[ A'(w)=100 - 2w = 0 \textrm{ when } w=50 \]

     Calculus and algebra both allow us to determine that the ideal rectangular pen for our critters is a square. (Although a more advanced form of calculus, called the calculus of variations, allows us to conclude that to maximize the area per perimeter, you should construct a circular fence -- a corral!)

  2. What if we can use an existing wall, e.g. the side of a long barn? What would the dimensions be? What do you think?

     Now the two dimensions are related by \[ 2w+l=200 \]

     so \[ l=200 - 2w=2(100 - w) \]

     Therefore \[ A(w)=2w*(100-w) \]

     No need to differentiate: this is just twice the previous equation, so it has the same critical point: \[ A'(w)=100 - 2w = 0 \textrm{ when } w=50 \] But now the length is 100m. You might think of this as two of the previous square pens glued together!

  3. The point is that these sorts of problems, when they can be formulated as functions, present opportunities for "optimization"; and the derivative is the tool that will help us locate the extrema, or "optimal" values of something.

     Generally we seek the global maximum or the global minimum -- which we have found in the cases above. Because those functions were quadratics, we know that they have only one point on their graphs where the derivative is zero -- and no points where their derivatives don't exist (although there were boundaries beyond which we couldn't go -- no lengths or widths were to be negative, for example).

     

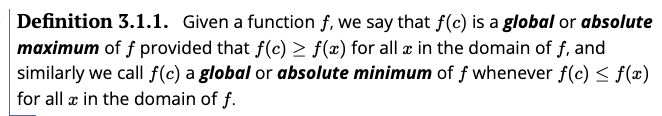
     One other important consideration is the domain. In those problems, the dimensions had to be positive. So we could have constrained the solutions to be where both $w>0$ and $l>0$.

     This sets up the possibility for the maximum or minimum to be at the border (as is true in this case -- the global minimum is 0 -- if we run the fencing the whole length, so that it's all length, with $w=0$. This results in a fence that Fido won't like at all!

     Furthermore, however, we might have local "extrema" (maxes or mins), that, while larger than their neighbors, give Fido only a local advantage -- but a better solution could be found elsewhere in the domain:

     

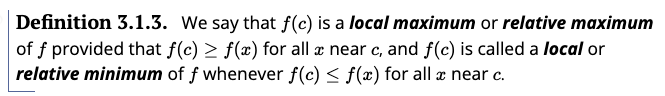
  4. Now let's consider a more pathological function: that of the preview for this section:
     

     and this set of images showing (some of) the kinds of things that can go wrong (at least in the case of a continuous function -- if you introduce discontinuities, things can get uglier):

     

     Figure 3.1.5. From left to right,

     1. a function with a relative maximum where its derivative is zero;
     2. a function with a relative maximum where its derivative is undefined;
     3. a function with neither a maximum nor a minimum at a point where its derivative is zero;
     4. a function with a relative minimum where its derivative is zero;
     5. and a function with a relative minimum where its derivative is undefined.

  5. There are two important tests in this section which we can deduce from the graphic above:
     1. The first derivative test: Let $c$ be a critical number of continuous function $f$.
        • If $f^\prime$ changes sign from positive to negative at $c$, then $f$ has a local maximum at $c$.
        • If $f^\prime$ changes sign from negative to positive at $c$, then $f$ has a local minimum at $c$.
        • If $f^\prime$ does not change sign at $c$, then $f$ has neither a max nor a min at $c$.

     2. Second derivative test: Suppose $f^{\prime\prime}$ is continuous near $c$.
        • If $f^{\prime}(c)=0$ and $f^{\prime\prime}(c)>0$, then $f$ has a local minimum at $c$;
        • If $f^{\prime}(c)=0$ and $f^{\prime\prime}(c)<0$, then $f$ has a local maximum at $c$.

  6. Let's try out Activity 3.1.2 from this section, and then I'll turn you loose to work on your worksheet.

  7. Worksheet for 3.1