Day 24, Mat128: Calculus A

0. Key
1. You need to observe that the function \(x^4\) fails the horizontal line test (that is, a give \(y\) value has more than one \(x\) value that gives rise to it); therefore, should we reflect that graph, the reflection would fail the vertical line test. The solution is to restrict the domain to some sensible subset of the actual domain.
2. All you needed to do here is to reflect the graph over the line \(y=x\); but carefully! Note in particular that
   1. the function and its inverse only touch (or cross) on the line \(y=x\); and
   2. if \((x,y)\) is a point on the graph of \(f\), then \((y,x)\) is a point on the graph of \(f^{-1}\).

3. This one was a little tricky; but first you needed to compute \(g'(x)\), and a fair bunch of you forgot the chain rule!

   The second "secret" is to write \(g'(x)\) in terms of \(g\) (because that makes the calculation of \(g'(g^{-1}(x))\) easy, since \(g(g^{-1}(x)) = x\).

1. The first derivative test: Let $c$ be a critical number of continuous function $f$.
   • If $f^\prime$ changes sign from positive to negative at $c$, then $f$ has a local maximum at $c$.
   • If $f^\prime$ changes sign from negative to positive at $c$, then $f$ has a local minimum at $c$.
   • If $f^\prime$ does not change sign at $c$, then $f$ has neither a max nor a min at $c$.

2. Second derivative test: Suppose $f^{\prime\prime}$ is continuous near $c$.
   • If $f^{\prime}(c)=0$ and $f^{\prime\prime}(c)>0$, then $f$ has a local minimum at $c$;
   • If $f^{\prime}(c)=0$ and $f^{\prime\prime}(c)<0$, then $f$ has a local maximum at $c$.
   • If $f^{\prime}(c)=0$ and $f^{\prime\prime}(c)=0$, then the case is indeterminate.

Here's the graph of the derivative mentioned in the activity: \[ g'(x) = \frac{(x+4)(x-1)^2}{x-2} \]

What does the graph of the derivative look like as \(x \rightarrow \pm \infty\)?

We'll go over the solutions on Wednesday, before your quiz. These functions are a little tricky: it pays to have something to help you graph them as you work on these exercises.

• We begin with the big idea: we think that there is some function that underlies the blooming time of the cherry trees, on average.

  We might expect that "the arrival of spring" is the big indicator: when the climate is screaming that spring has arrived, things begin happening such as the arrival of robins and the blooming of cherry trees.

  There are perhaps a lot of "sub-climatic things" (such as total rainfall, or average cloud cover, or average temperature) that will impact the blossoming, but there is assumed to be some "trend" function that captures the overarching pattern.

• We will consider several mathematical models that capture the early blooming. In particular, we would like to establish whether
  1. Indeed there is evidence for earlier blooming
  2. An estimate for the number of days earlier the blooming is occurring (over the historical average), and
  3. What kind of model works best to capture the trend.

• We might start by examining the data, to see if we can identify anything in particular: what do you think?
  

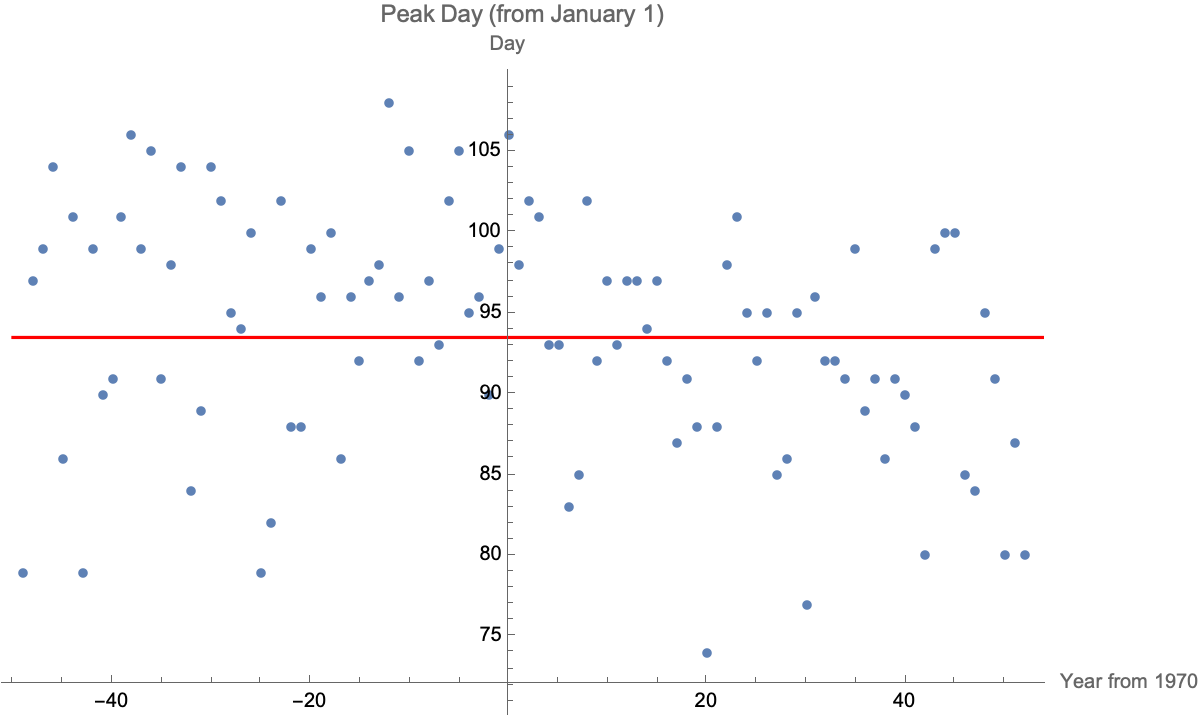
  (the red line is the average across all years)

• A typical objective function (linear model): \[ E(m,b) = \sum_{i=1}^{n} (y_i - (m x_i + b))^2 \] We seek to minimize the "sum of squared errors" (this is the sum of the squared errors between the model and the data over all the data).

  Ah ha! We see "to minimize" -- we seek an extremum.

  The problem here is that the objective function is a function of two variables (\(m\) and \(b\)); we're doing "univariate calculus".

  What we know, however, is that this procedure will lead to a choice of \(b\) so that the line passes through the mean of the data: \((\overline{x},\overline{y})\). This allows us to determine one of the parameters (we choose \(b\)), so it reduces to something like \[ E(m) = \sum_{i=1}^{n} (y_i - f(m;x_i))^2 \]

• The strategy is then to differentiate this function \(E\) with respect to \(m\), and set its derivative equal to zero; we'll then have an extremum (since all the terms are quadratics, they can get infinitely big, but only as small as zero): using the chain rule on this big sum, we get \[ E'(m) = \sum_{i=1}^{n} 2(y_i - f(m;x_i))f'(m;x_i) = 0 \] In fact, we're guaranteed to have a minimum (which is what we want).

• The basic linear model is simple, which is good, but gives us no idea of the historical average. It does, however, provide evidence that there has been a real change in blooming date, and provides our first guess of how dramatic the change has been over 100 years: about seven days (7.02047, to be precise -- but that's silly, given the noise in the data -- better to say "about seven days"!).

  But it makes no sense as time continues to go further back: the blooming dates wouldn't have continued getting later and later, if the climate were relatively stable.

• The basic quadratic model argues for inflection -- it is, indeed, an umbrella. But it makes no sense over 100 years, and for the past -- the historical average would have been roughly constant, if the climate were more constant.

• My choice for the final model would be a "cutpoint model" (either the linear or the quadratic models). They both show an "historical average" of around 95.5 days from the start of the year.

• Based on the entire 102 years of data, the average peak bloom date for Washington's cherry blossoms is April 4.
• Peak bloom date for the cherry trees is occurring earlier than it did in the past. Since 1921, peak bloom dates have shifted earlier by approximately seven days. The peak bloom date has occurred before April 4 in 16 of the past 20 years.
• While the length of the National Cherry Blossom Festival has continued to expand, the Yoshino cherry trees have bloomed near the beginning of the festival in recent years. During some years, the festival missed early peak bloom dates entirely.