Day 41, MAT115

Chase has a nice mathematically-based logo:

There are always critics, of course

This will be our intuitive definition of a Fractal:

A world within a world!

This key notion is more formally called "self-similarity": "a self-similar object is exactly or approximately similar to a part of itself (i.e. the whole has the same shape as one or more of the parts)."

• Our Fibonacci spirals
• The tree diagram of the rabbit problem that gave rise to the Fibonacci numbers.
• Often these arose out of the idea that we carry out a process, then "do it again, do it again"....

• Here's a suitable mascot for this unit: Bessie the fractal cow:
  

• Have you ever lined up a couple of mirrors and seen an infinite number of copies of yourself disappearing off into the distance?

  Well, try my funhouse mirror generator: make your own funhouse mirror image, using my web interface and your own image, and I'll post them to our website.

• World's Most Famous Fractal (Benoit Mandelbrot, Novel Mathematician, Dies at 85: 10/14/2010 -- a good image of him)

1. It's a process or graph that possesses "self-similarity".
2. It often possesses a simple and recursive (or iterative) definition -- that is, we do something, and then we "do it again!"

It turns out that nature loves fractals, just like it loves Fibonacci numbers.

• We'll start with the famous "Koch" fractal:
  1. Start with a straight stick.
  2. Replace the middle third of the stick with a little "tent" -- two third-length sticks.
  3. Do it again and again!
  

  This fractal becomes infinitely long, but in a confined space! Very strange.... but this type of strange behavior is typical of fractals.

• Here are some more lovely examples (including the Koch fractal, but check out the beautiful bushes!).

• The Sierpinski triangle is an area fractal.
  • First deterministically:
    • fractals by addition
    • fractals by subtraction
    • fractals by subtraction (a local copy)

  • After we're finished removing all that stuff, how much area is left in the triangle?

The Chaos game - generating fractals using random movement!

• Once again, simple rules lead to complex objects. This time, however, we don't proceed methodically, but rather haphazardly - and yet we still produce the complex images!
  • with 10 points
  • with 100 points
  • with 500 points
  • with 1000 points
  • with an infinite number of points!

  Here's a better version of that, that has more general options.

  From randomness comes order; from simple rules comes complicated objects! Then all hell broke loose....

• This section involves several "complex" ideas: complex numbers, Newton's method for finding roots of functions, and fractals.
  • What is a complex number? It is a "complex", made up of multiple things. It has a real part, and an "imaginary" part. The real part is an ordinary real number. The imaginary part is based on the number i, which represents the "positive" square root of -1.

    The complex number z is the sum of a real and a complex part:

    where x and y are just ordinary real numbers.

    Sometimes mathematicians just propose something, and hope that it's useful!

    Complex numbers live in a plane, with a real and an imaginary axis:

    

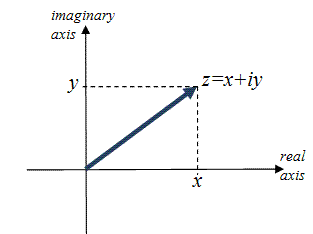
    We need to realize that i is the solution of a mathematical equation: .

  • What is Newton's method?

    First of all, it's named for Sir Isaac Newton, one of the greatest mathematicians of all time, born in England on Christmas Day, 1642 (in the year that Galileo died).

    Secondly, it's about finding "roots" of equations. That is, for example, if we want to find where , Newton's method can help. It will get as close to a solution as we wish, but may never get to the exact solutions, which are .

    Newton's method works by shooting straight lines off a point on the graph of the function, looking for the places where the function's graph crosses the x-axis. Those values of x are the roots.

    This applet will give you a good idea of what Newton's method is about, illustrating Newton's method's attempts to find solutions of

    

    This polynomial has three real number solutions, and Newton's method can find them all. But starting at different places along the number line we find different values of the root. This is a crucial concept.

    For some polynomials, however, Newton's method won't work if we start with a real number approximation to the root. This is illustrated by putting the function (with derivative ) into this applet. It hunts for the place where the curve crosses the x-axis, but can't find it! That's because the answers are actually complex, imaginary even!

• The last notion puts them together, and forms a fractal.

  To find those values of the roots, we'd have to start with a complex guess, and then use Newton's method -- and then it would work! But we'd be starting off with a point in a plane, instead of a point along a line.

  Deterministic fractals: delve into an infinite, dynamic world, created by a simple mathematical process: the function whose roots we seek is

  

  We know that there's only one real number solution: . But there are also two complex solutions (turns out that the highest power of z -- 3, in this case -- tells you how many roots your equation is going to have).

  • a simple rule
  • repeated over and over and over.... but
  • simple rules, intense content!
  The simple rule is Newton's method applied to every point in the complex plane. The color represents which root the method will find of the three -- so there are three different colors).

  As Strogatz suggests, there are three big basins where the results are pretty boring -- you converge to the nearest root -- but along the boundaries of the three regions, all hell breaks loose! Or rather a fractal breaks loose, "psychedelic hallucination" (p. 57)....

  And as you zoom in on the "psychedelic hallucinations", you see hallucinations within hallucinations.