- Your second homework assignment is due today (Babylonian numbers).
- Your first homework assignment is returned.
- For the elevator problem, most of you realized
that 8 people would assure two with a common
birthday; but almost no one could show that 4
people on the elevator would guarantee you an
advantage (by about 2 to 1).
#people probability of having no common "birth day of the week" 1 1 2 0.857143 3 0.612245 4 0.349854 5 0.149938 6 0.042839 7 0.006120 8 0.000000Remember: just do it! How can you attack this problem? Do something (and make sure you explain what you've done -- it's not enough to just write a number down...).
Can you eliminate any answers? For example 2 is too few (don't bet with just two people on the elevator);
and 6 is more than you need (no one will bet you at 6, because they'll know that they'll likely lose).So we have some intuition, and you can report that.
- You seem to be doing pretty well with the trees, and
primitive counting.
But I'm seeing a lot of the most common problem: some folks forget the last "non-triangle" entry.
So the strings were
- 32=100000
- 63=111111
- 97=1100001
- 42=101010
- 85=1010101
- 177=10110001
- For the elevator problem, most of you realized
that 8 people would assure two with a common
birthday; but almost no one could show that 4
people on the elevator would guarantee you an
advantage (by about 2 to 1).
- You have another assignment due next time (Mayan
numbers). I've also assigned a new one for next
Tuesday, so you should be keeping busy!
- Please read the following
So the way that these readings will work is to fill in some details on what we discuss in class, and I'll expect you to have read them for additional information.There will be some questions on the tests that refer to these readings. Feel free to bring up things that you have read during our class time.
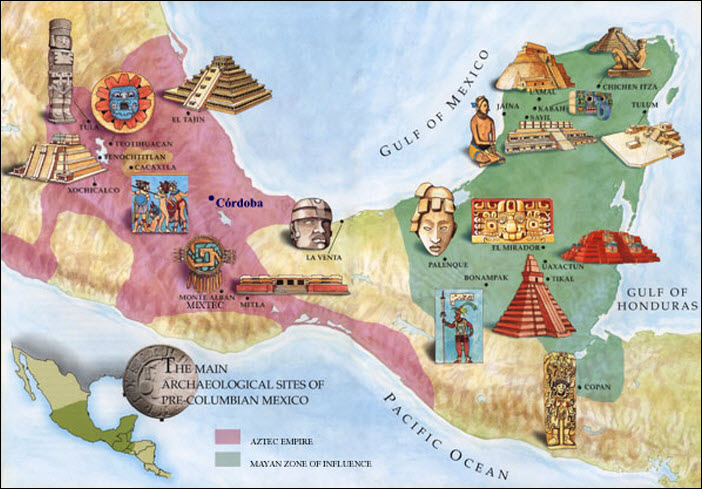
- Let's have a look at what the Mayans were doing over in
the new world:
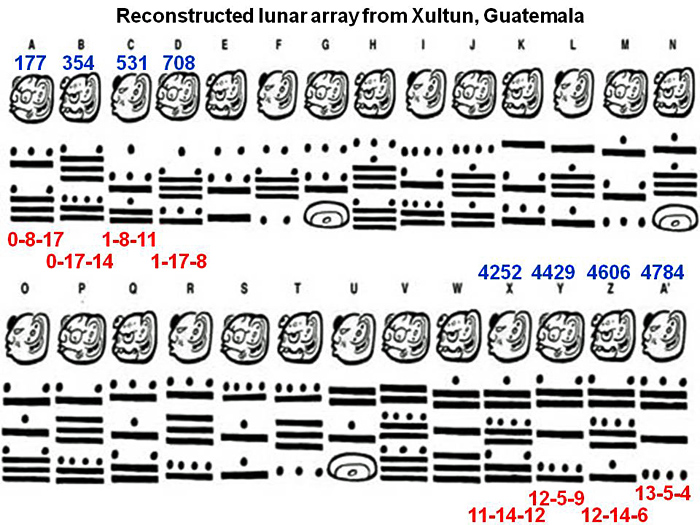
- Take a look at this Mayan lunar calendar:
 (pdf)
(pdf)
"The Maya also made their own very accurate measurement of the solar year, putting it at 365.242 days. The latest computations give us the figure of 365.242198: so the Maya were actually far nearer the true figure than the current Western calendar of 365 days (which, with leap years, gives a true average of 365.2425)." From The Universal History of Numbers, by George Ifrah.
How can we make sense of the numbers that are appearing?
- How would the Mayans write the number we call 1729?
- I'll write something in Mayan, and you tell me what it is in our number system.
- What distinguishes the Mayans from the Babylonians?
- Let's do a few examples with Mayan numbers: write the
following in Mayan
- 37
- 694
- 1034
- 141664
- Take a look at this Mayan lunar calendar:
- Now I want to invite into our math circle my
very close friend, the Great Fraudini!
- How does the game work?
- Can you win at the game? You should be able to do it every time!
- Here's the handout for the cards, if you want to print off another copy.
- I'd like you to play with a partner, taking turns playing the roles of contestant and Fraudini. Make sure you can do it!