Day 25 in Mat115

Today:

• Announcements:
  • Your graph and mobius homeworks are returned.
    • All simple graphs with five vertices.

  • Your link and knot drawing exercise is due.

  • No new homework for Thanksgiving? Why knot! (sorry)

    You do have a knot identification homework due on Tuesday, after the holiday.

  • Don't forget that your logo day is coming soon.

    You'll type up a one-page description of your logo, focusing on both mathematical and personal aspects of your logo.

    Then you will present your logo to the class, and you'll have about 2 minutes to talk about it. That will be a competition, with the top winners getting GOHF cards.

  • Some company logos with a mobius theme:
    
    
    
    

• Today's Question of the day:
  "How can we tell two knots apart, or decide that they're the same?"

  Last time we got one answer: Reidemeister moves. Today we get a second answer: tricolorability.

• Before we go on, I want to say a little about how knots are actually useful:
  • Trefoil knots are in your heart (the following images are from a paper by Art Winfree at the University of Arizona, on "excitable media"):
    • 

    • 

    • 

    • 

    • 

  • My dad carved mathematical objects, including this surface for Art Winfree (related to heart arrhythmias):

    

• Last time we learned about twist knots:

  There are two more knots that we need to know, that are not toroidal (torus knots -- that we get by using twisted bands, which we can think of as donut knots). They're called twist knots.

  • There are two different ways to think about making the trefoil knot: as a
    1. torus knot, and as a
    2. twist knot.
    Let's draw it in these two different ways.

  • The figure-eight knot has four crossings, as does Solomon's "knot", but it's a true knot. This is the first (interesting) instance of a knot and link with the same number of crossings.

  • We already know one 5-crossing knot: the cinquefoil.
    • Actually, there are two kinds of 5-knots
    • To help you, we have the Rolfsen Knot Table
    • The cinquefoil knot
    • The 3-twist knot
    • How can we tell them apart? Are they really different? For that we need to study knot equivalence, and our primary tool, the Reidemeister moves.

    How do we show that two knot projections ("squiggles") are the same knot ("knot equivalence")? That's the job of the Reidemeister moves.

    1. What are the Reidemeister moves?
       • Tools for showing that two projections (pictures) of knots really show the same knot.
       • Names of the moves reflect the number of strands involved. A Strand is a piece of a knot picture that goes from undercrossing to undercrossing, with only overcrossings inbetween.
       • Reidemeister moves preserve the knot -- they don't change the knot. We're not cutting -- we're just going to shove parts of the knot around.

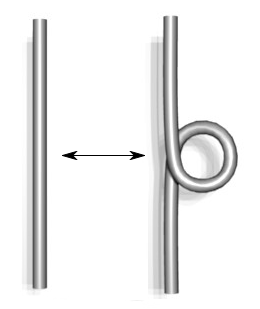
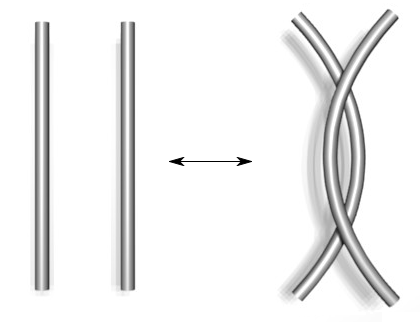
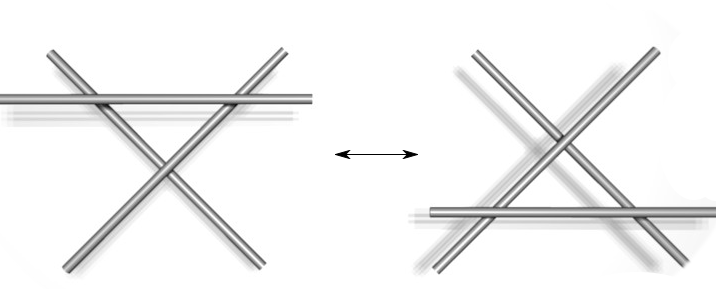
       • Type I	Type II	Type III

    2. Using the Reidemeister moves
       1. to turn a projection of an unknot into another more complicated appearing unknot:

          We'll just try a few with a string, to see what we can learn.

       2. Now let's use these three moves to create equivalent versions of the trefoil knot, but using each of the three Reidemeister moves.

       3. A figure-eight knot is equivalent to its mirror reflection (a trefoil knot is not equivalent to its mirror!)

       4. Turning a more complicated appearing unknot into a simple circle unknot. (Here it is as a powerpoint presentation.)

    3. Reidemeister moves and Tricolorability
       1. Tricolorability: "A knot is tricolorable if each strand of the knot diagram can be colored one of three colors, subject to the following rules:
          1. At least two colors must be used,
          2. at most three colors are used, and
          3. at each crossing, the three incident strands are either all the same color or all different colors.

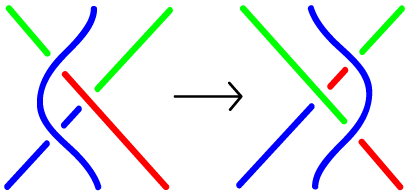
       2. Tricolorability is preserved by Reidemeister moves:

          Reidemeister Move I is tricolorable.	Reidemeister Move II is tricolorable.	Reidemeister Move III is tricolorable.

       3. Therefore, if the projection of one knot is tricolorable and the other isn't, they're different knots (because we can't get from one to the other via Reidemeister moves).

       4. Theorem: there are at least two different knots.
          1. The unknot is not tricolorable ("At least two colors must be used");
          2. The trefoil knot is tricolorable:
          3. The figure-eight knot is not tricolorable (it requires four colors):
          4. Danger: many knots are tricolorable -- being tricolorable doesn't mean that your knot is the trefoil knot -- but it does mean that your knot is not the unknot!

             Links can be tricolorable, too -- for example, the unlink is tricolorable! (That's just two circles, one lying on top of the other, as in Borromean rings.)

• Speaking of "colorful", let's look at some "Knot Mosaics" (key point: it's all about "overs and unders"!):
  

  (an example of Solomon's Knot -- which you might notice is actually a link!)

  • Celtic Knot Mosaic Examples: (not quite the same idea, but pretty! And again, you'll see that there are links contained therein -- including Borromean rings)
    • Triangular paper (in case you want to try making some of those).

  • Knot Mosaics
    • help us to draw Borromean Rings, for example: use your Mosaic Graph Paper to create your own version of the Borromean Rings.
    • Rectangular Mosaic Tiles and symmetry
    • We can use them to make any knots: try your hand at
      • the trefoil knot
      • the figure-eight knot