Day 26 in Mat115

Today:

• Announcements:
  • Your link and knot identification exercise is due.

  • Your link and knot drawing exercise is returned. Recall the instructions:

    ---

    Draw by hand, and well, all four links we've now encountered:
    • The unlink
    • The Hopf link
    • The Solomon's knot (actually a link)
    • The Borromean rings
    and all three torus knots:
    • The unknot
    • The trefoil
    • The cinquefoil
    You will be judged on correctness, and neatness.

    Note: Do not write "I can't draw!" on your paper. I get that all the time, and I don't care. I'm not much of an artist either, but if I spend the time, I can do a good job. You can, too. You need to draw carefully, and well; so find a way to do it!

    ---

    • If I can't see all of the overs and unders, it's zero. I can't tell what it is.
    • The biggest mistake was "Hopf-linking" Borromean rings. Each ring is under another, and on top of the third.

  • Don't forget that your logo day is coming next Tuesday.

    You'll type up a one-page description of your logo, focusing on both mathematical and personal aspects of your logo.

    Then you will present your logo to the class, and you'll have about 2 minutes to talk about it. That will be a competition, with the top winners getting GOHF cards.

• Today's Question of the day:
  What is a fractal?

• Before we get to fractals, however, let's just review what we were doing last time:
  1. We were talking about how to distinguish knots. We learned that there must be two knots (in fact there are infinitely many!), because the trefoil is tricolorable, and the unknot is not; yet tricolorability is unchanged by Reidemeister moves (i.e. all pictures -- projections -- of a given knot are the same -- either tricolorable or not, depending on the knot). So the trefoil can't be the picture of an unknot, and so we have at least two knots. No surprise. You probably think that mathematicians spend a lot of time proving the obvious!
  2. Tricolorability
  3. Reidemeister moves
     1. We can use the Reidemeister moves to figure out what kind of knot appears on the cover of this book.
     2. Preserve tricolorability: to help you to learn these, I invented a knot to go with each Reidemeister move.

• Fractals
  • The concept of fractals is the most modern mathematics that we'll study. We've worked our way up from the Babylonians all the way to the 21st century.

    This will be our intuitive definition of a Fractal:

    A world within a world!

    This key notion is more formally called "self-similarity": "a self-similar object is exactly or approximately similar to a part of itself (i.e. the whole has the same shape as one or more of the parts)."

  • Some examples you have seen before: (Notice how these arise out of the idea that we carry out some process, then "do it again, do it again, do it again"....)
    • Our Fibonacci (and golden) spirals
    • Dual Platonics: e.g. a tetrahedron within a tetrahedron within a tetrahedron.... Maybe cooler are the other pairs, where we alternate solids (cube then octa), then repeat the process.
      

    • The tree diagram of the rabbit problem that gave rise to the Fibonacci numbers.

    • Additional examples you might have seen before:
      • Here's a suitable mascot for this unit: Bessie the fractal cow:
        

      • Russian Dolls
      • World's Most Famous Fractal (Benoit Mandelbrot, Novel Mathematician, Dies at 85: 10/14/2010):
      • The A0 Paper Fractal

        "A paper" is something you've no doubt encountered before: it's the long sheets we occasionally use (usually "A4" paper), which is far more common in Europe.

        "A paper" is constructed so that, if folded in half (do we say the long way or the short way?), you get a sheet which has exactly the same shape -- that is, the ratio of its side lengths is the same as the original sheet.

        

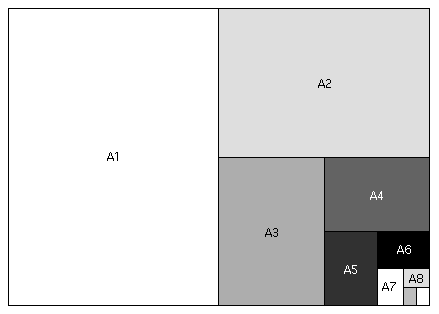
        Let's see what the dimensions of A paper must be so that this requirement is fulfilled....

        Call the long dimension of the A1 paper above , and the short dimension 1.

        • Then what are the dimensions of the A2 paper, according to the design of A paper?
        • What is the value of ?

        Why not an A0 paper spiral? Let's try that.... This is the spiral, created using non-squares each time:

        

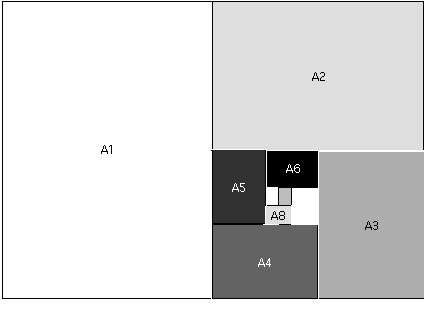
        In both cases there's "the world within the world". Both are fractals.

  • So what is a fractal? A couple of things we'll generally see:
    1. It's a process or graph that possesses "self-similarity".
    2. It often possesses a simple and recursive (or iterative) definition -- that is, we do something, and then we "do it again!"

  • Let's check out a beautiful gallery of natural fractals.

    It turns out that nature loves fractals, just like it loves Fibonacci numbers.

  • Building deterministic fractals with sticks
    • Consider the famous "Koch" fractal:
      1. Start with a straight stick (the "initiator").
      2. Replace the middle third of the stick with a little "tent" -- two third-length sticks (the "generator").
      3. Do it again and again!
      

      Let's make a variation of that. Use your Triangular paper, and a stick along the edge that's 9 units long. Best to use a pencil with a good eraser! Mistakes will be made....

      Move up as you create the next level (or iteration) of Koch fractal. This could go on forever!

      What happens to the length of the Koch fractal? Let's compute it for the first few cases.

      How big of an area contains the Koch fractal? A finite area. And how long is it? Infinitely long! This is kind of puzzling.... But, in a way, it helps to explain things like DNA: if you twist something up enough, you can get a very long thing in a tight space!

      Alternatively: instead of triangular tents, we could make square tents. What happens if we do that? Again, use a power of 3 (27 is good) to make your fractal (because we're cutting things into threes).

    • Here are some more lovely examples (including the Koch fractal, but check out the beautiful bushes!).

      If that link won't work, maybe this L-System Fractals page will.

  • Building deterministic fractals with areas:

    The Sierpinski triangle is an area fractal.

    • Triangular paper is good for Sierpinski....
    • First deterministically:
      • fractals by addition
      • fractals by subtraction
      • fractals by subtraction (a local copy)
      After we're finished removing all that stuff, how much area is left in the triangle?

    • Now let's introduce a little bit of randomness (this means that the fractal is not formed deterministically anymore): Sierpinski's triangle again:

      The Chaos game - generating fractals using random movement!

      • Once again, simple rules lead to complex objects. This time, however, we don't proceed methodically, but rather haphazardly - and yet we still produce the complex images!
        • with 10 points
        • with 100 points
        • with 500 points
        • with 1000 points
        • with an infinite number of points!

        Here's a better version of that, that has more general options.

        From randomness comes order; from simple rules comes complicated objects! Then all hell broke loose....

    • Deterministic fractals: delve into an infinite, dynamic world, created by a simple mathematical process:
      • a simple rule
      • repeated over and over and over.... but
      • simple rules, intense content!

  • Let's have a look at a recent (January, 2015) addition to the fractal family: the Harriss fractal). It starts with the golden rectangle, and then makes a slight change.

  • I've found a Java program (from here) that we can use to visualize fractals using what is known as the "L-System" (Lindenmayer Substitution Fractals).
    • a simple rule
    • repeated over and over and over.... but
    • simple rules, intense content! Fantastic creations are a snap.

    You might try creating some of your own.

    The Koch fractal is this:

    1. Axiom: f
    2. Rules: f=f+f--f+f
    3. Start Angle: 90
    4. Turn Angle: 60

  • Now back to Pascal's triangle. What does it have to do with Sierpinski?

    Let me re-introduce you to Vi Hart, who will talk us through the relationship between Pascal and Sierpinski. She talks really fast, however!

    Then we'll try her method to see how, within Pascal, there's Sierpinski....

    • even plus even is even
    • odd plus odd is even
    • even plus odd is odd
    So Vi remarks that we don't need to actually calculate the numbers in Pascal's triangle to see whether the next number will be even or odd. Let's do an E/O Pascal's....

• Links
  • L-System Based Fractals (and a local copy).
  • This one might work when Java won't: L-System Fractals