- Today's quiz covers symmetry, which we continue discussing today.
- I've assigned a short reading
about symmetry.
- "In their recent books, Richard Prum and Michael Ryan synthesize
research on animals and people, exploring possible evolutionary
explanations for our own aesthetic tastes. Ryan is particularly
interested in the innate sensitivities and biases of our neural
architecture: He describes how our visual system, for example, may be
wired to notice symmetry."
How Beauty Is Making Scientists Rethink Evolution: The extravagant splendor of the animal kingdom can't be explained by natural selection alone -- so how did it come to be?
- Hermann Weyl has this to say in the concluding paragraph of his book Symmetry:
"Symmetry is a vast subject, significant in art and nature. Mathematics lies at its root, and it would be hard to find a better one on which to demonstrate the working of the mathematical intellect."
- We discussed the results of the exam; there is a key, if you need to figure things out. Or come to see me!
- There are several forms of symmetry, two of which we studied in
our four
page handout:
- reflective
- rotational
It's sometimes funny, or jolting, when symmetry breaks down:
But, as David noted, there was a certain "organized asymmetry" to what Fred and Ginger were doing here, which was beautiful in its own way.
- Humans are bilaterally symmetric; but, more generally,
- Life loves symmetry (Symmetry
of life forms on Earth)
A phenomenal scientist and artist, Ernst Haeckel, discovered and documented many of the radiolaria, such as this one (Spumellaria):
These have a beautiful three-dimensional rotational symmetry - and we're headed into three-dimensions today!
- Symmetry can be useful: graphic designers
"fake" the true recycling symbol with one arrow, which they
copy and rotate to make their "faux recycling symbol" (the true
one is on the right, and you'll see that the arrows are not all
the same).
It can be used to make fancy dances more interesting, by copying movements across the dance floor (translational symmetry) -- e.g. contra or square or line dances.
Today we consider the Platonic solids, which possess a great deal of symmetry: they're super-symmetric solids.
- We begin our discussion with the convex regular
polygons:
"A regular polygon is a polygon which is equiangular (all angles are equal in measure) and equilateral (all sides have the same length). Regular polygons may be convex or star."
- Last time we didn't quite get to the following questions in the
2-Dimensional plane:
- What is the most symmetric rectangle?
- What could you do with a heptagon?
- How many regular polygons are there?
- What kinds of symmetry do they possess?
- Which regular polygons can be used exclusively to "tile" the plane, like a bathroom floor?
- Using symmetry in a process, to build complete
graphs. Let's try \(K_6\)!
- As an example, consider regular convex hexagonal
graph paper, which represents a tiling of the plane by a
regular convex polygon. You see these kinds of tilings in bathrooms.
Bees have the same idea:
- The honeycomb is actually solid -- three-dimensional. The tubes
have hexagonal walls. But the comb is not Platonic.
A cube is an example of a Platonic solid. It's the one we're most familiar with, so let's start with that.
A Platonic solid is a solid for which
- All faces are congruent (identical) convex regular polygons, and
- Each face, each edge, and each vertex is exactly equivalent to every other face, edge, or vertex (respectively).
They're super-symmetric!
The Five Convex Regular Polyhedra (Platonic solids) -- thanks Wikipedia! Tetrahedron Hexahedron
or CubeOctahedron Icosahedron Dodecahedron 
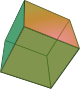
fire earth air water universe - What do these have to do with Plato? According to Weyl, "Plato, in the
dialogue Timaeus, associates the regular pyramid, octahedron,
cube, icosahedron, with the four elements of fire, air, earth and water
(in this order), while in the pentagondodecahedron he sees in some sense
the image of the universe as a whole."
Some nice illustrations from Weyl's book.
- What's wrong with six sided polygons, and beyond? Consider the
hexagonal graph paper, of the tiling of the plane: why can't it be folded up
into a solid?
The answer involves Euler's formula, as Weyl discusses.
- What can you do with these solids?
- Play basketball? Three Sides to This Story: Knicks Dust Off
Phil Jackson's Triangle Offense, from the New York Times:
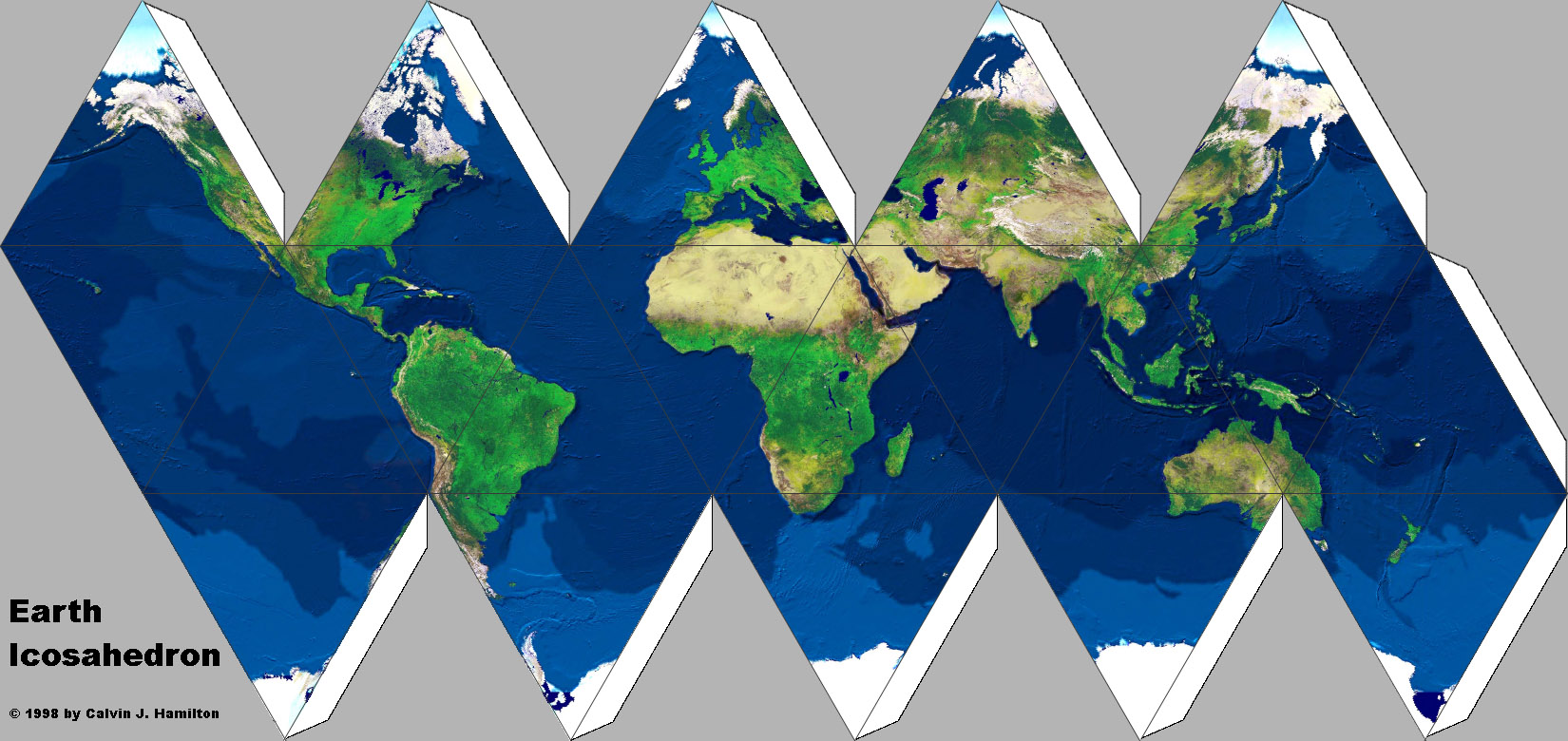
- Map the Earth?
The Platonic solids allow us to make "flat spheres" (sort of!):
- Johannes Kepler thought that the orbits of the planets (of which
five were known at the time) were somehow related to the various
Platonic solids, as shown in
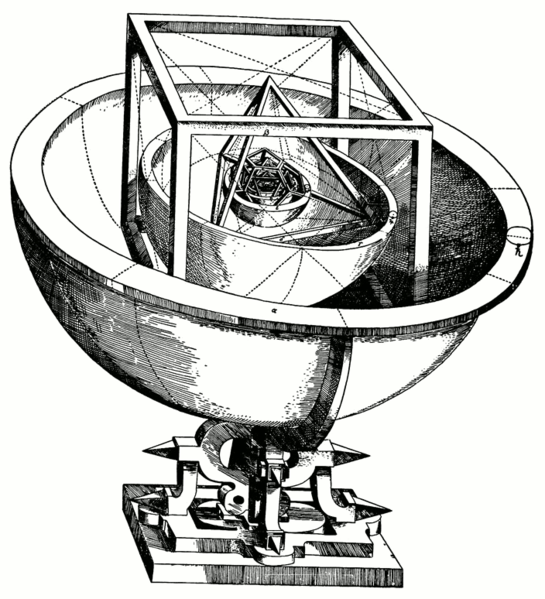
"The six spheres each corresponded to one of the planets (Mercury, Venus, Earth, Mars, Jupiter, and Saturn). The solids were ordered with the innermost being the octahedron, followed by the icosahedron, dodecahedron, tetrahedron, and finally the cube. In this way the structure of the solar system and the distance relationships between the planets was dictated by the Platonic solids."
And then Uranus was discovered, and there was not a sixth Platonic solid. And so science evolves....
- Something interesting to share: great images from Linus Pauling's and Roger Hayward's The Architecture of Molecules (a book created especially for young people, and based off of Pauling's article in the 1964 Proceedings of the National Academy of Sciences.
From Pauling's paper:
Molecular architecture may be said to have originated in 1874, when J. H. van't Hoff and J. A. le Bel independently formulated the brilliant postulate that the four valence bonds of the carbon atom are directed approximately toward the corners of a regular tetrahedron. It was extended into inorganic chemistry in 1893, when A. Werner suggested that in many inorganic complexes six atoms are arranged at the corners of a regular octahedron about a central atom, and that other geometrical structures are represented by other complexes.These are some higher quality images than my scans:
- So what can you do with a dodecahedron? Make a calendar!
- So what can you do with an icosahedron?
- Look like a super-brainy, cool scientist! (From the October 7th, 2011 New York Times)
- Create amoeboid protozoa Circogonia icosahedra:
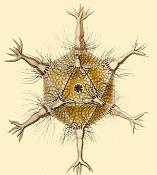
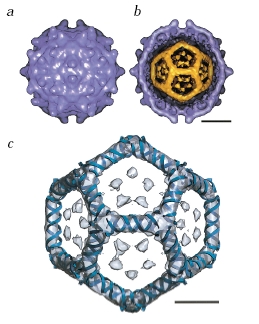
- Make viruses:
- The Cliff Notes Version...
"An array of viruses. (a) The helical virus of rabies. (b) The segmented helical virus of influenza. (c) A bacteriophage with an icosahedral head and helical tail. (d) An enveloped icosahedral herpes simplex virus. (e) The unenveloped polio virus. (f) The icosahedral human immunodeficiency virus with spikes on its envelope."
- Or Bacteriophages and Virions
- The Cliff Notes Version...
- Dodecahedral
- Viruses:
- Viruses:
- More critters:
- Canine Parvovirus
- bacteriaphages:
- Play basketball? Three Sides to This Story: Knicks Dust Off
Phil Jackson's Triangle Offense, from the New York Times:
- Now let's use what we can deduce of Platonic solids to fill in the
following table:
# of Vertices Edges Faces faces at each vertex sides at each face Tetrahedron Cube Octahedron Dodecahedron Icosahedron What conclusions can we draw from this data? Is there a pattern? (Of course there is!:) The pattern leads to the concept of "Duality":
- Each Platonic solid has a "twin" -- called its dual -- which we can discover from the table.
Here's nature being all dual: This pastel drawing of a compound of Molybdenum Dichloride is from Pauling's book:
- Each Platonic solid has a "twin" -- called its dual -- which we can discover from the table.
- Symmetry, by Hermann Weyl (Princeton University Press, 1952)
- All wallpapers (there are 17 of them!)
- Symmetry Handout Key (annotated)
- Symmetry of lifeforms on Earth
- A fun reading on symmetry
- Hexagonal Paper