- This week's quiz will be over symmetry/Platonic Solids.
- We discussed the Platonic solids.
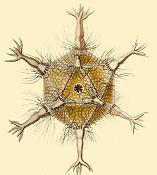
- We examined a few more examples of "Platonic solids in nature",
e.g. viruses, bacteriophages, etc., and the Amoeboid protozoa
Circogonia icosahedra:
- We had a quiz:
- Key
- Median: 8
- Let's talk about a few things that folks did well at, as seen on the key.
- Some of you brought your mirrors (used your reflective phone screens, etc.). Good thinking!
- Before we leave the Platonic solids, let's review the situation so
far:
- The table:
# of Vertices Edges Faces faces at each vertex sides at each face Tetrahedron 4 6 4 3 3 Cube 8 12 6 3 4 Octahedron 6 12 8 4 3 Dodecahedron 20 30 12 3 5 Icosahedron 12 30 20 5 3 - Each Platonic solid has a "twin" -- called its dual -- which we can discover from the table.



Dualing examples:
- The table:
- How can we draw the Platonic solids on a sheet of paper? We project them onto the paper.
- The cube you've undoubtedly done before.
- The tetrahedron can be drawn to be a "distorted" Mercedes symbol
- Here
are all the solids. Practice drawing them! Where's the duality?
-
In the following graphic, you see another way to represent these
objects in two-dimensions, by unfolding them:

- So here's our story to this point: we started off with regular
polygons in two dimensions, and discovered that there were
similarly super-symmetric objects in three-dimensions.
People have made use of these solids for many unusual purposes: for example, someone you know constructed this Platonic grape arbor on his farm in Canada:

Salvador Dali's works included a fair amount of math (such as The Sacrament of the Last Supper):

- In a gorgeous
video, Prof. Carlo Sequin begins by showing how to start
from regular polygons -- two-dimensional regular polytopes --
and build all the Platonic solids -- three-dimensional
polytopes; but he eventually shows how to build all the regular
polytopes in all higher dimensions!).
We'll watch about 7 minutes of this, but I encourage you to watch the rest when you can:
- A little further along in the video, Prof. Sequin describes all
the
symmetries of the four-dimensional version of the
octahedron.
Can you guess https://en.wikipedia.org/wiki/Octahedral_symmetry? The question is, in how many ways can you rotate or reflect an octahedron to get what appears to be the same octahedron (which which, in fact, involved mixing it up by moving vertices, edges, and faces around)?
- Finally, towards the end of the video, Prof. Sequin uses
duality to obtain the third class of polytopes.
Back to regular polygons for the moment:

- an equilateral triangle?
- a square?
- a pentagon?
- translations (e.g. wallpapers), including glide reflections. Here is a nice description of these "Transformations of the plane".
- symmetry of scale
- Wallpaper is often made up of a single repeated pattern,
sometimes reflected, and then translated over the
entire wall periodically to make an attractive
impression.
In how many different ways (from the standpoint of distinctly different symmetries) can one create such a pattern?
Suppose you have a design, of a mouse say, such as the prototypes of the mice of Mathemalchemy:

Nine of the possible wallpaperings are shown on the bakery wall of Mathemalchemy:

And throughout the exhibit you can see various other "wallpaperings", in different media.
The seventeen distinctly different wallpaper groups: (the following images are taken from this Wikipedia page, Wallpaper group)

















- Today's Question of the Day:
What is the most beautiful rectangle? - We've made some Fibonacci spirals -- but today we want to make
Golden spirals.
- As we move toward the so-called "golden mean" and "golden
rectangle", we'll start with a nice Fibonacci spiral (we've done this
already: see this
site for more on these spirals).
Ordinarily we build the Fibonacci spiral by building bigger and bigger rectangles. The shapes of the rectangles change as we go along, in such a way that the ratio of side lengths are Fibonacci numbers. Let's look at the sequence of the ratios....
So let's recap the spiral building process, with a focus on those side ratios.
- Start with a piece of graph paper (the wide way), and darken the square in the 10,10 spot (ten from the left, ten down from the top). You might want several colors, if you've got them -- might as well make this pretty!
- Rule: attach the largest square you can: first left, then down, and then continue in a counter-clockwise fashion.
- As you add each square you create a new rectangle. Compute the ratio of side lengths (larger over smaller).
- Do it again, do it again, do it again! (You could do it forever -- but we run out of paper.)
- What do you notice about the dimensions of the rectangle? It's the
ratio of those dimensions that interests us most -- the ratio
of dimensions (larger to smaller) dictates the shape of the
rectangle. Two rectangles that have the same ratio have the
same shape.
1x1 1/1= 2x1 2/1= 3x2 3/2= 5x3 5/3= 8x5 8/5= 13x8 13/8= 21x13 21/13= 34x21 34/21= - The thing we are approaching is the so-called golden rectangle,
whose side-lengths are in the ratio called "the golden
ratio". But we will derive the golden rectangle in a different
way -- the way that the Greeks did it! When we're done, we'll
have also defined the golden mean, aka the golden ratio.
- Begin with a rectangle.
- Remove the largest square possible from the rectangle, to leave a rectangle.
- If the rectangle that results has exactly the same shape as the original
rectangle, then that rectangle is golden:
However if we look back at the Fibonacci spiral sequence of rectangles as they're growing, we see that they're tending toward a "golden rectangle".
-
If you did your Fibonacci reading (and of course you did!), you know
that the ratios of successive Fibonacci numbers tend toward a certain
number, which is called the "golden mean" or "golden ratio":
\[
\varphi=\frac{1+\sqrt{5}}{2} (\approx 1.618033988749895)
\]
Let's show that this golden ratio is, in fact, the side-length ratio of the golden rectangle described above. And our secret weapon will be your old friend, that old favorite, the quadratic formula!
While we might think about the Fibonacci spirals as being created by attaching squares, the golden rectangle is created by removing squares. We just do things backwards....
But each rectangle remaining is a perfect copy of the original! In contrast to our Fibonacci spiral, in which case each was successively more beautiful, each of these is a perfect copy -- smaller, yes, but perfectly the same. This is an example of symmetry of scale. And while we can, of course, tile the floor with these, we're going to need some tiles of vastly different sizes (some getting incredibly small).
We can build beautiful rectangles by pasting squares together, or we can define beautiful rectangles by taking them away....
- Now what can we do with these ideas?
Here is a somewhat silly example -- A Fibonacci spiral fractal comic I made recently, which I have entitled "Flirting with Death Spiral". Infinite fun! I'll be having you make one of these yourself, so you'll want to think of a good photo to use....

(sidelengths: 466x288, with ratio 1.6180555555555556!)
By the way, Salvador Dali's image is sized 334x208: side ratio, 1.6057692307692308
- One last example of tiling with the exact same shape of scaling sizes is provided in a beautiful video which we may watch today, if we have time.
- We've made some Fibonacci spirals -- but today we want to make
Golden spirals.


