- James has a concert coming up,
Thursday, April 18, at 1:45pm.
- Today's quiz is over basic knot and link identification.
Knots actually have a scientific importance. Of course chemists like to mess around with them:
- We're going to work on the homework
assignment about distinguishing knots. If you've already
started, great; otherwise, it's your lucky day!
- Reminder and last call: You had a
homework that was to be a small part of the exam: to make
some pretty knots, and take a picture, and send to me.
If you would like to submit that, do so by midnight tonight!
Then we'll have another art contest.
(If you already sent me your picture, you're done!)
- Also a reminder that we're just a little over two weeks from our
project and logo
demonstrations (the last week of class).
- I've just got to share this article from the New York Times yesterday: Sticks. And the People Who Love Them.. Some of these stick-lovers have even created an Instagram account for Official Stick Reviews.
See? Sticks are beloved, too! And stick fractals are even cooler!
- I introduced you to the "RCO" -- Really Cool Object -- which
brings together the Borromean rings, golden rectangles, and
Platonic solids (an icosahedron), the most beautiful piece
of mathematics I know:

- Then it was on to a discussion of the Reidemeister moves:
- We observed that some knots and links have the same minimal number
of crossings (e.g. the figure-eight knot and Solomon's Knot); how do we
distinguish them? In that case, it's easy: one is a knot, and one is a
link. Just check if you have just one continuous curve, or two.
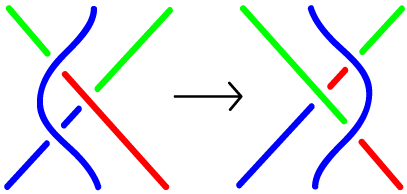
But in the case of knots it's not so easy. We have two tools, and the first is the Reidemeister moves:



Type I Type II Type III - Reidemeister moves preserve the knot -- they don't change the
knot. We're not cutting -- we're just going to shove parts of
the knot around.
- Here's my summary of
the moves.
Here's a picture of an unknot, which could trick you -- but you're not deceived, because you know your Reidemeister moves, in particular the R1 move.

- We observed that some knots and links have the same minimal number
of crossings (e.g. the figure-eight knot and Solomon's Knot); how do we
distinguish them? In that case, it's easy: one is a knot, and one is a
link. Just check if you have just one continuous curve, or two.
Before moving on to tricolorability, let's review how to use the Reidemeister moves, and see how the two concepts relate:
- Let's use the three moves to create to determine what kind of knot
this
is.
- A figure-eight knot is
equivalent to its mirror reflection (a trefoil knot is not equivalent to its
mirror!)
- Reidemeister moves and Tricolorability
- Tricolorability:
"A knot is tricolorable if each strand of the
knot diagram can be colored one of three
colors, subject to the following rules:
- At least two colors must be used,
- at most three colors are used, and
- at each crossing, the three incident strands are either all the same color or all different colors.
- Tricolorability is preserved by Reidemeister moves:
Reidemeister Move I is tricolorable. Reidemeister Move II is tricolorable. Reidemeister Move III is tricolorable. - Therefore, if the projection of one knot is
tricolorable and the other isn't, they're different
knots (because we can't get from one to the other via
Reidemeister moves).
- Theorem: there are at least two different knots.
The unknot is not tricolorable ("At least two colors must be used") The trefoil knot is tricolorable: The figure-eight knot is not tricolorable (it requires four colors): "The figure-eight knot is not tricolorable. In the diagram shown, it has four strands with each pair of strands meeting at some crossing. If three of the strands had the same color, then all strands would be forced to be the same color. Otherwise each of these four strands must have a distinct color. Since tricolorability is a knot invariant, none of its other diagrams can be tricolored either." (source) 


- Danger: be careful what you conclude:
- Links can be tricolorable, too -- for example, the unlink is
tricolorable! (That's just two circles, one lying on top of
the other, as in Borromean rings.)
- many knots are tricolorable -- in fact, infinitely
many! -- so being tricolorable doesn't mean that
your knot is the trefoil knot -- but it does mean that
your knot is not the unknot, for example.
So, for example: if you've got your picture of a knot down to three crossings, and it's not tricolorable, then it's the unknot.
- And among knots and links with five crossings or fewer, only the trefoil and the unlink are tricolorable.
- Links can be tricolorable, too -- for example, the unlink is
tricolorable! (That's just two circles, one lying on top of
the other, as in Borromean rings.)
- Let's have a look at some examples knots, and try to determine
which is which.
- We'll start with knots of up to 7 crossings. We already
know about those with five or fewer crossings.
Which of the 6- and 7-knots are tricolorable? (There are three.)
- Then we'll consider "A Knotty Tale", and try to determine all the knots (and links).
- We'll start with knots of up to 7 crossings. We already
know about those with five or fewer crossings.
- Tricolorability:
"A knot is tricolorable if each strand of the
knot diagram can be colored one of three
colors, subject to the following rules: