- I moved our second exam up on our schedule and assignments page, to April 3rd from April 10th. It makes a little more sense to me, in terms of what material I plan to cover on it.
- There's a quiz today at the end of the hour, over primes and prime factorization.
- Did anyone watch "Prime
Target"?
"If he succeeds in finding a pattern in prime numbers, he will hold the key to every computer in the world."
- We talked a little more about graphs, in particular the
complete graphs which we used to represent numbers.
Definition: a graph is a collection of points ("vertices") as well as a collection of arcs ("edges" -- each of which joins two points).Definition: If every vertex in a graph is connected to every other (different) vertex by a single arc, we call it a complete graph.
Each number, considered as a complete graph, encompasses all the numbers that go before it:
Name of graph: 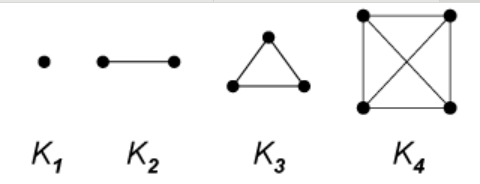
Number of arcs: \(T_0=0=\frac{0(1)}{2}\) \(T_1=1=\frac{1(2)}{2}\) \(T_2=3=\frac{2(3)}{2}\) \(T_3=6=\frac{3(4)}{2}\) and we drew a few more (\(K_7\) and \(K_8\)).
- I described Gauss's method for adding up the numbers from
1 to 100, to illustrate that the sum of the first \(n\)
counting numbers -- \(T_n\) -- is given by
\[
T_n = \frac{n(n+1)}{2}
\]
This number is related to the number of arcs in \(K_n\), but
notice that the number of arcs of \(K_n\) is the previous
triangular number \(T_{n-1}\).
- The new thing introduced was "primitive counting", addressing the question
How do we count without counting? Historically, according to our reading Early Concepts of Number and Counting, folks used ideas like
- Tallies (Did anyone draw a cartoon of the Baker and the woman buying bread, comparing their tally sticks?)
- using body parts -- "one hand" of sheep, say -- meaning five sheep. (Did anyone notice any rhyme or reason to the ordering of the body parts?)
- knotted strings (Did anyone draw a knotted string like that of "The Example 3643", but for the number 1294?)
- cairns
- How do the South Africans mentioned count to numbers above 100?
- But we talked about a method called "counting by partitions"
- Let's suppose you need to let the King know how many sheep you
have (but you were never taught how to count). You do, however,
know how to make one-to-one correspondences:
- divide your sheep equally ("one for you, one for me") into
two pens: either there is one sheep left over, or not; either
they "correspond", or not.
You make a note of whether there is a leftover sheep or not -- maybe you make a mark, like a "1" or a "0". This is all you have to do to communicate the number to the King!
But you must also pay attention to the direction in which you write the marks.
- Send all the sheep in pen two (and any "left over") out to pasture, and then
- You divide the sheep in pen one into pens one and two: i.e., just do it again! And again, and again, and.... until you get down to a pen with just one sheep in it.
- Now let's think about how we might record the results to
send to the King. Here was an example, using a
"ternary tree" (another kind of graph):
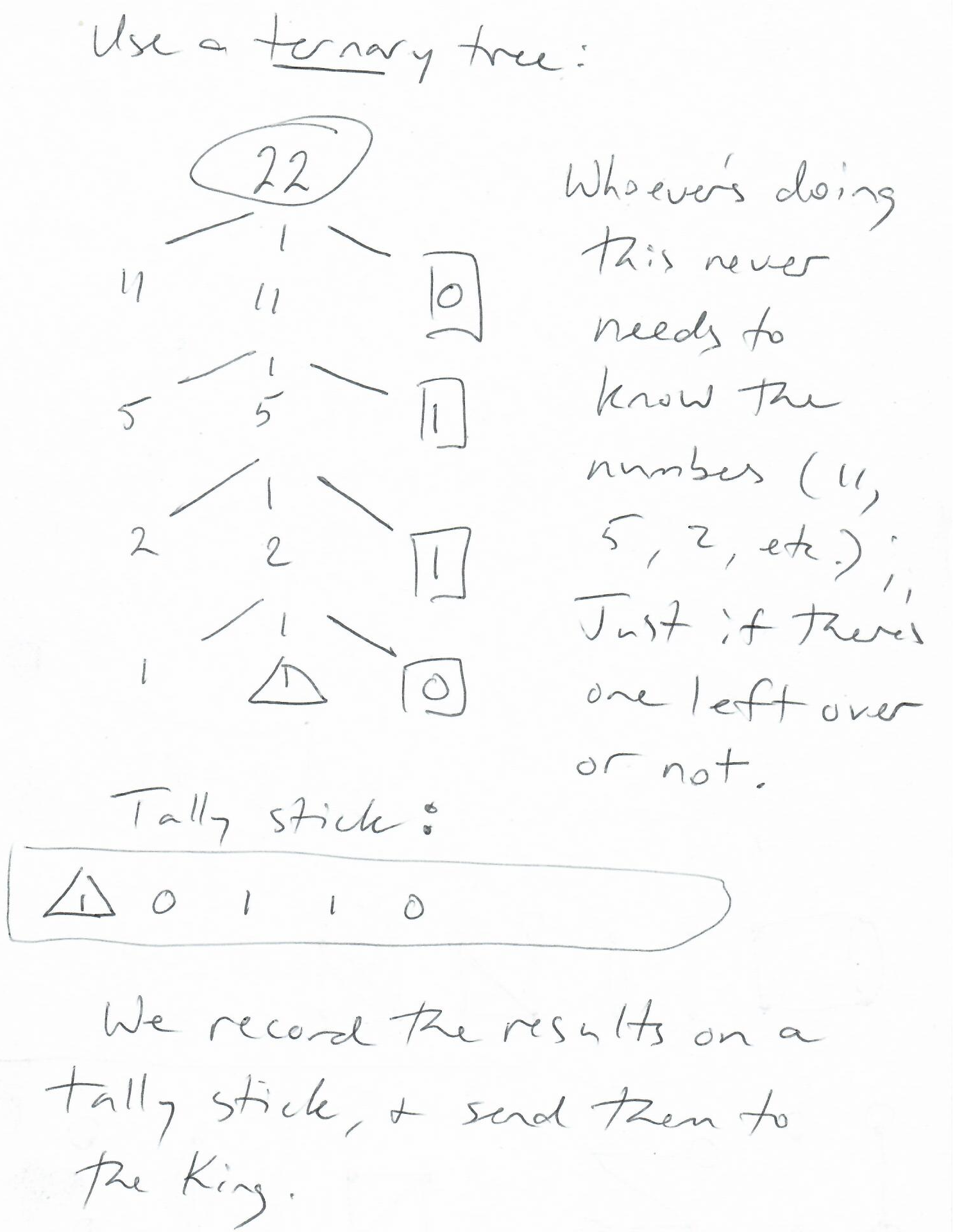
- divide your sheep equally ("one for you, one for me") into
two pens: either there is one sheep left over, or not; either
they "correspond", or not.
- Can you go backwards? How many sheep is meant by 10011?
- Let's suppose you need to let the King know how many sheep you
have (but you were never taught how to count). You do, however,
know how to make one-to-one correspondences:
- Today we move on from the primes, composites, and polygonal numbers, and introduce the next topic with a magic trick. Yes, you too can amaze and astound your friends and family!
- So yes, today we'll have a visit from my very close and very old
and dear family friend, The Great and Powerful Fraudini!
It turns out that The Great Fraudini can read anyone's mind -- so long as they're thinking of a number between 1 and 63, and they're willing to play a little card game with him. So let's see how this works....
- Rules of the game: you show your "victim" every card. If they see their number on it, they say "Yes"; otherwise they say "No". Then you tell them their number!
- Can you become as powerful as The Great Fraudini? (You should be able to do it every time!)
- Here's the handout for the cards. You need a set of cards to play!
- FYI: It turns out that I'm a really bad magician -- because I
always give away my tricks!:) But I want you to be able to
perform the trick, so I'm giving it away.
So in case you don't have a magic trick up your sleeve, I'm giving you one!
However I want you to think about it before I just give it away. Take a look at your cards, and see if you can figure out how The Great Fraudini is doing it....
What do you notice about the cards? (Look for patterns!)
- I always tell my students in MAT115 that my real course objective
is to help you to make money by gambling. I'm going to teach
you some tricks that might win you a drink somewhere,
somehow....
But I also always tell my students that gambling is foolish, unless you have inside information. So I'm all about giving you the inside information. But generally, and (in particular):
A lottery is a tax on people who are bad at math. - Now time for a quiz....
- American Bandstand dances to Gimme Some Lovin', a hit by The Spencer Davis Group: here's their version.
- List of musical works in unusual time signatures
- Blue Rondo a
la Turk, by Dave Brubeck: illustrating
how to play a piece in 9/8.
Watch Dave Brubeck's leg, counting out the rhythm....