- I hope that you had a good, relaxing holiday.
- Your quiz is returned. Some of you were stymied by the word "stymied":
sorry about that! If I use a word, and you don't know what it
means, feel free to ask.
Here is an example of a quiz that earned full credit. There were many.
- (3 pts) Who are the three main characters in the "Six Fish" video, and
what are their roles?
In particular, how are they critical to the action?
- Humphrey -- takes the order, and "factors it"
- Ingrid -- can't get the order right -- doesn't hear the factors
- Ernie -- explains counting, and the one-to-one correspondence between the counting numbers up to six and the orders of fish.
- (3 pts) What helpful cadence might the hotel manager use if there
were 24 fish?
Give at least two different possibilities, and decide if one is better in any way than the other.
- Perhaps the most straightforward answers involved factoring 12, such as this answer which compared 4*6 (four sets of six) and 6*4 (six sets of four).
- Or perhaps 2*12 or 8*3. But are either of those good?
- Someone
suggested giving the order to a tune with twelve
beats, twice; or to 8 measures with 3 beats.
They also suggested drawing the fish order for part 3, which was a great answer.
- Someone proposed a couple of cool cadences, one that reminded me of a tune (I mistakenly remembered it as a Sam and Dave tune, but....) She proposed doing 24 as \[ 4-1-4-1-4-1-4-1-4 \] but that reminded me of the tune Gimme Some Lovin', which Steve Winwood, of The Spencer Davis Group, performs Live! Listen for \[ 5-1-5-1-5-1-5-1 \]
- Someone suggested doing three eights as sevens + ones, \[ 7-1-7-1-7-1 \] as in a Blake Maislin commercial (at 20 seconds).
- (4 pts) Two parts:
- How is the hotel manager stymied by having 13 orders of fish?
The problem is that 13 is prime, so isn't evenly divisible by any number less than 13.
- What might you suggest the manager do if faced with that order?
- Someone suggests adding an accent beat to make 13.
- Some suggested having the characters learn to count!:)
- 13: Dave Brubeck's Take
Five gets us a 5/4 rhythm; his Blue
Rondo a la Turk shows us how to play in 9/8
(illustrating
how to play a piece in 9/8).
Watch Dave Brubeck's leg, counting out the rhythm....
We could do the same kind of thing to get to 13/8, with say \[ 12-12-123-123-123 \] or \[ 123-123-123-12-12 \]
- Nine Inch Nails's tune The Becoming is purportedly in in 13/8 time.
- How is the hotel manager stymied by having 13 orders of fish?
- (3 pts) Who are the three main characters in the "Six Fish" video, and
what are their roles?
- Apple TV+ debuts trailer for new conspiracy thriller "Prime
Target," starring Leo Woodall and Quintessa Swindell, premiering on
January 22 -- tomorrow!
"If he succeeds in finding a pattern in prime numbers, he will hold the key to every computer in the world."
- Our quiz Thursday will be over prime factorization. So I might
give you a problem like this:
Is 481 prime? Demonstrate, if so; if not, find its prime factorization.
What's your first move? (After pulling out your calculator....)
- We reviewed prime factorizations (primes, composites, and the theorem which assures us that all counting numbers greater than 1 are either prime, or can be written as a product of primes in one way). One is the loneliest number, but Two can be as bad as one; it's the loneliest number since the number one.
- I then proved that all counting numbers are interesting
- We talked about how prime numbers tend to get lonelier and lonelier as they move off to infinity.
- Mathematicians suspect that there are an infinite number of the so-called "twin primes" (such as 3 and 5, 5 and 7, 11 and 13, 137 and 139, and so on....). As long as you're floating out there in the vastness of space, it's nice to have a partner.
- We moved on to how we think about numbers like "six". I suggested
that we think of numbers as diagrams, which we call
graphs.
Definition: a graph is a collection of points ("vertices") as well as a collection of arcs ("edges" -- each of which joins two points).An edge can even join a vertex to itself, which is called a loop in a graph.

Definition: If every vertex in a graph is connected to every other (different) vertex by a single arc, we call it a complete graph.
Each number, considered as a complete graph, encompasses all the numbers that go before it:
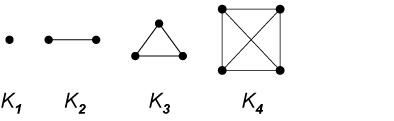
- We drew a few more, up to 6 -- \(K_6\), that is. And we saw the
divisibility of a number popping out. Here's the method:
- We usually start with our points on a "regular polygon" (more about those later): like an equilateral triangle, or a perfect square. This maximizes symmetry!
- First you draw from a point to its neighbor (and then do it again, do it again, ....)
- Then you draw from a point to the point two away (and then do it again, do it again, ....)
- Then three away, etc., etc.
- If by doing so you don't hit all the points before you get "home", you've discovered a divisor of the number!
Let's draw \(K_7\) and \(K_8\):
- I mentioned that the tetrahedron is actually a three-d version the complete graph with four vertices, \(K_4\), as well as a model for the Methane molecule.
- Trees are examples of graphs. Trees have two properties that
graphs don't possess in general:
- They have a special point (vertex), called "root";
- They have no "circuits" -- no paths that lead off from a point and then arrive back eventually, as in the tetrahedron.
That means that there's a unique path between any two vertices (which is not true for tetrahedron, because there are circuits in that graph).
- We found a pattern to the number of connections (arcs, or edges) the
complete graphs have as the number of points grow.
Finley figured out that the number of arcs grows by the addition of the next integer, which is how the triangular numbers grow (and someone (Meghan?) came up with a formula):
\(K_n\) \(arcs(K_n)\) 1 \(0=\frac{1(0)}{2}\) 2 \(1=\frac{2(1)}{2}\) 3 \(3=\frac{3(2)}{2}\) 4 \(6=\frac{4(3)}{2}\) 5 \(10=\frac{5(4)}{2}\) 6 \(15=\frac{6(5)}{2}\) n \(\frac{n(n-1)}{2}\) 
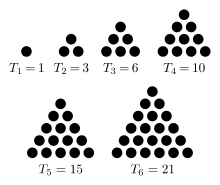
Mathematicians are pattern seekers: we look for patterns, and then try to explain those patterns.
- I just had time at the end of the hour to point out the tail end
of my material, so let me go into a little more detail today, before we
move on to something new:
The problem of triangular numbers is related to another story, about a little boy who became the greatest mathematician of all time.... Carl Friedrich Gauss ("the Prince of Mathematicians").
The story is told in a different way in one of your reading assignments (Rock Groups).
I hope that you noticed the pretty geometric way of envisioning this in "Rock Groups", where the sum is the natural numbers from 1 to 10 (55):

Carl may have done it a different way, which I want to share.
- In terms of its personality, 6 is a triangular number: a number,
like 55, which can be represented as a isoceles right triangle (above),
or like those perfect stacks of balls above.
Numbers (like squares), which can be represented by some geometric figure are called polygonal numbers. Another interesting example given in Rock Groups, are the perfect squares: \(n^2\) can be thought of as the sum of the first \(n\) odd natural numbers:
\(1+3+5+7+9\) 
\(=25\) These mysterious properties are parts of the personalities of numbers. What's your favorite natural number's personality? If your favorite number is 36, then you're lucky: it's both square and triangular!




































= 1 + 3 + 5 + 7 + 9 + 11
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 =



































- You already know the answer: with a one-to-one correspondence. But
let's go into the weeds a bit, and I'll illustrate some alternative
versions of that. In particular, let's get into some Primitive counting....
- Today I teach you how to count! You're probably thinking "Heck,
Sesame Street taught me how to count; Ernie taught me how to count last
week!"
But how might "primitive" people have counted? (Ernie's not primitive enough; neither is he a person.) You won't be surprised to learn that we will be using a tree to help us.
- We have some good ideas of how "primitive" people counted,
generally via a one-to-one correspondence of some sort
(hopefully you read the article I assigned
for homework, Early Concepts
of Number and Counting).
- Tallies
- using body parts -- "one hand" of sheep, say -- meaning five sheep.
- knotted strings
- cairns

- But today I want to describe a method of "counting by partitions"
that
Patricia Baggett and Andrzej Ehrenfeucht described at the 2011
National Math Meetings (based on a suggestion from 1817!):

- Let's suppose you need to let the King know how many sheep you
have (but you were never taught how to count). You do, however,
know how to make one-to-one correspondences:
- divide your sheep equally ("one for you, one for me") into
two pens: either there is one sheep left over, or not; either
they "correspond", or not.
You make a note of whether there is a leftover sheep or not -- maybe you make a mark, like a "1" or a "0". This is all you have to do to communicate the number to the King!
But you must also pay attention to the direction in which you write the marks.
- Send all the sheep in pen two (and any "left over") out to pasture, and then
- You divide the sheep in pen one into pens one and two: i.e., just do it again! And again, and again, and.... until you get down to a pen with just one sheep in it.
- Now let's think about how we might record the results to
send to the King.
- divide your sheep equally ("one for you, one for me") into
two pens: either there is one sheep left over, or not; either
they "correspond", or not.
- The easiest way to illustrate the counting method is via a
tree.
Let's see how we might use a tree to represent the solution to the "22" counting problem: we'll use a ternary tree (three children branch off of a parent, rather than just two -- as we've seen in the binary trees for prime factorization).
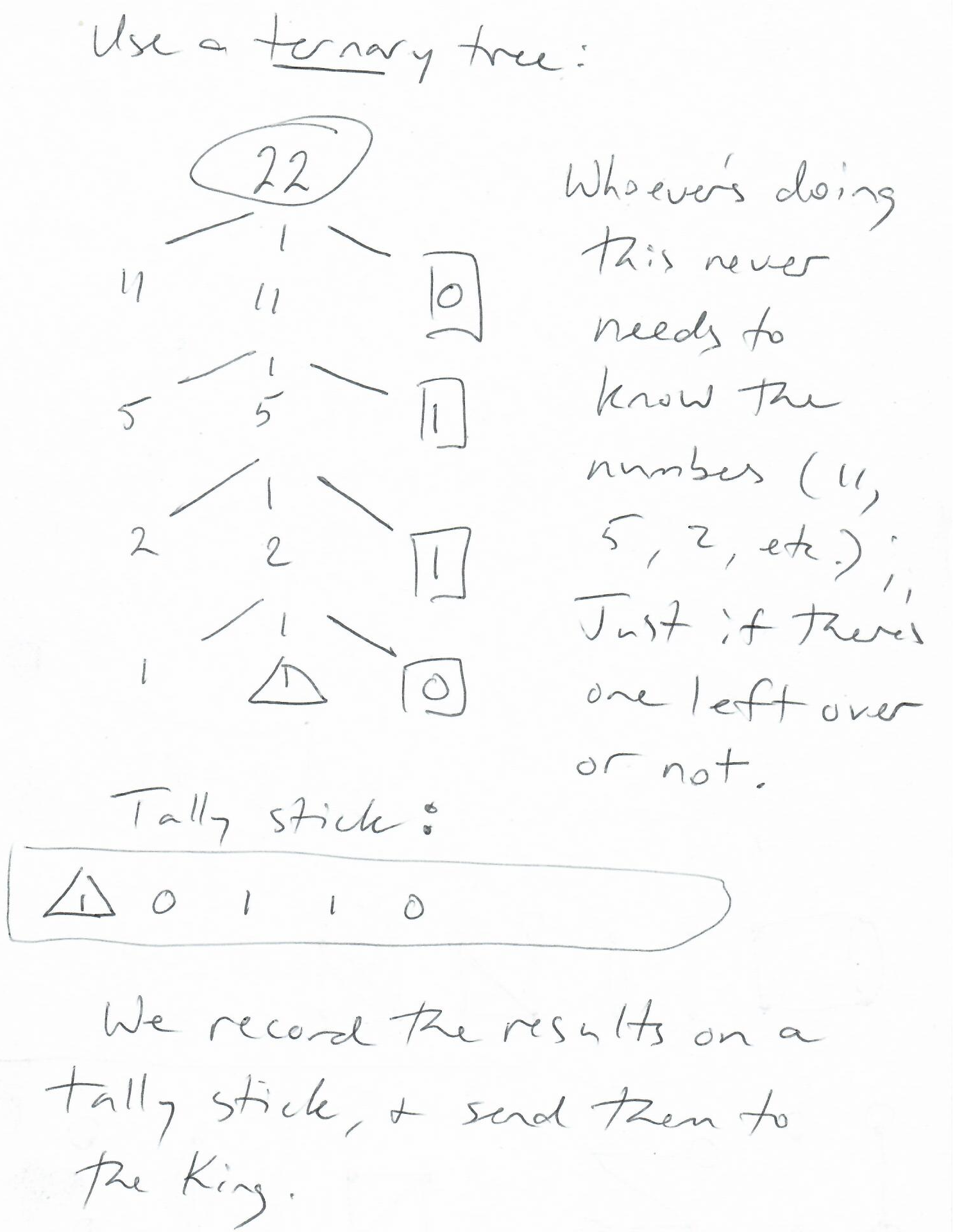
I say "Whoever's doing this..." -- I mean, "Whoever's doing this primitive counting...." This is presumably someone who doesn't know how to count -- at least not the way we do -- but they can tell if there's one left over (and write "1") or not (and write "0").
Notice that we eventually have a single sheep in a pen, and that's when we're done. We have to write a "1" for the final sheep, to indicate that there's "one leftover".
Then the answer will be written as 1, 0, 1, 1, 0. That is, from the bottom up, left to right. This is important! We have to have a consistent scheme for writing (or otherwise recording our results -- perhaps on a knotted string).
So how do we write
- 9 sheep
- 31 sheep
- 54 sheep
- Can you go backwards? How many sheep is meant by
- 1,0,1,1
- 1,1,0,1,1,0,0
- 1,0,0,1,0,1,1,0,1
(Notice that, while there can be either a 0 or 1 at the right end, there is always the "1" on the left -- meaning the last sheep standing!
Can you rebuild the tree using these "tally sticks"? If so, you can get a job in the King's counting house.
- If you're afraid of sheep, think about counting pennies. When I
was little I counted lots of pennies (I collected them, and
would get rolls from banks to look through -- when I was done I
had to put 50 pennies back into the rolls).
But rather than count out fifty pennies, I'd make a stack of 10, then four more stacks of exactly the same height (one-to-one correspondence). Five stacks of 10 makes 50. This is a similar idea....
If you have a lot of pennies, you could divide them in half, count half, and then multiply by two. But if you have one left over, you'd have to add that one.
If the half is still too many to count, do it again (on half), and so on -- until you get to the point where you can count "the half" (like if it gets down to 1 coin, say!:).
- Let's suppose you need to let the King know how many sheep you
have (but you were never taught how to count). You do, however,
know how to make one-to-one correspondences:
- Today I teach you how to count! You're probably thinking "Heck,
Sesame Street taught me how to count; Ernie taught me how to count last
week!"
- American Bandstand dances to Gimme Some Lovin', a hit by The Spencer Davis Group: here's their version.
- List of musical works in unusual time signatures
- Blue Rondo a
la Turk, by Dave Brubeck: illustrating
how to play a piece in 9/8.
Watch Dave Brubeck's leg, counting out the rhythm....