Day 3, MAT115R

• You will have a quiz today over our readings of "From fish to Infinity" (and the accompanying Sesame Street video).

  The prime factorization stuff will be part of next week's quiz.

  Let me know when we get to 5:45, in case I'm overly excited about something...:)

• Reminder: No class on Monday, for Martin Luther King, Jr. Day

• We talked some more about those chipmunks, who were celebrating the primeness or compositeness of their numbers:
  

  This shows that we could build a tree for 12 in more than one way: \[ 12=2*6=2*2*3 \] or \[ 12=3*4=3*2*2 \]

  In either case, we get the same prime factorization, or prime decomposition.

  But that \(13=2*5+3\), or \(13=2*6+1\), or \(13=3*4+1\), or... Nothing divides it evenly -- there's always something left over. Unless, of course, we consider itself and 1 -- \(13=13*1\). 13 is prime.

• We encountered some definitions (and I warned you that you need to know them, as well as any theorems we encounter!):
  • The counting numbers are the positive integers: 1, 2, 3, .... These are also known as the natural numbers.
  • A counting number is prime if and only if it has exactly two distinct divisors among the counting numbers: numbers 1 and itself.
  • It is composite if and only if it has more than two distinct divisors among the counting numbers.

  • Theorem (prime decomposition): every natural number (other than 1) is either prime, or can be written as a product of primes in a unique way, from smallest to largest.
  Notice that 1 is not prime, because there are not two distinct counting numbers that divide it; neither is it composite, because it doesn't have more than two divisors.

• We found that 150=2*3*5*5 is composite, constructing different trees.

• How are primes identified? Historically, the "Sieve of Eratosthenes" is the tool that was used, and watch this "animated solution" for the spirals!

  We found

  • The only two adjacent primes,
  • The triplet primes,
  • The twin primes,
  • "Spirals"

• To test which numbers are prime, we need only test those primes up to the square root of the number -- and no larger. If by that point no prime divides the given number, then the given number too is prime.

  Here is a list of the primes less than 100:

  2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

  This list would allow you to test any number for primeness up to 10000 (because its square root is 100...).

  Is 329 prime? It looks kind of primey...:) We only need to check primes up to 17, since \(\sqrt{329}\approx 18.14\), and the next prime is 19 which is greater than that.)

• So what about six? Strogatz in the article suggests that "...numbers are shortcuts for counting by ones...." (p. 5): so we might say that "six is a shortcut for counting by ones -- six times?"
• The key concept between the idea of number is the idea of "one-to-one correspondence": a perfect matching.

  ---

  Definition: a one-to-one correspondence is an association between two sets, so that each member of one set has a unique partner in the other set (and vice versa).

  It is the one-to-one correspondence between the fish and the numbers 1 through 6 (as shown in the video) that is the essense of "counting". It is dependent, of course, on the order of our numbers; that we present them in the proper order: 1, 2, 3, ....

  ---

• I ended with a preview of another way of thinking about the counting numbers, and we'll pick up there today.

1. One is the loneliest number, but
2. Two can be as bad as one; it's the loneliest number since the number one.
3. I can prove that all counting numbers are interesting, using order!

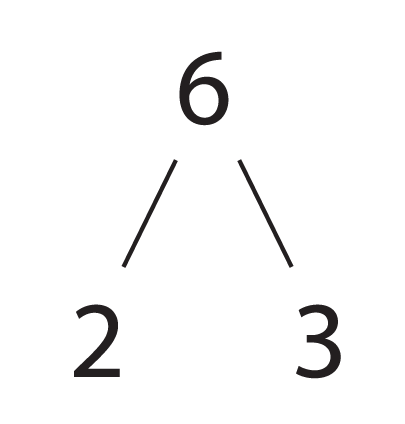
Other numbers seem very gregarious; they play well with other numbers (e.g. 6, which seems particular friendly with 2 and 3; or 12, which has lots of friends: 2,3,4,6!).

But how can we understand "6" without understanding "5" as well? (and thus 4, 3, 2, 1,...0?) We'll discover that 0 was pretty hard to understand from early on!

An edge can even join a vertex to itself, which is called a loop in a graph.

Definition: If every vertex in a graph is connected to every other (different) vertex by a single arc, we call it a complete graph.

Each number, considered as a complete graph, encompasses all the numbers that go before it:

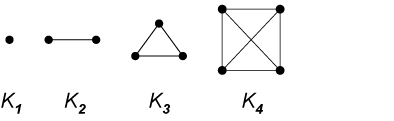
Let's draw a few more, however (at least up to 6!). And we'll see the divisibility of a number popping out. We're going to draw them by going around the horn:

1. We usually start with our points on a "regular polygon" (more about those later): like an equilateral triangle, or a perfect square. This maximizes symmetry!
2. First you draw from a point to its neighbor (and then do it again, do it again, ....)
3. Then you draw from a point to the point two away (and then do it again, do it again, ....)
4. Then three away, etc., etc.
5. If by doing so you don't hit all the points before you get "home", you've discovered a divisor of the number!

The picture of "four" (which is known as "\(K_4\)") has an unfortunate feature: its edges appear to overlap. We can alleviate the problem by pulling \(K_4\) out of the plane (two dimensions), and turning it into a three-dimensional animal (one of which I've brought with me today:

The tetrahedron (one of the Platonic solids, which we'll study down the road) is actually also the complete graph with four vertices:

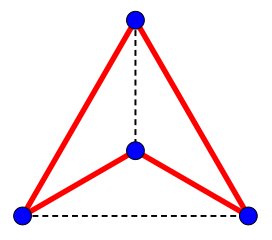
1. Do you see a complete graph with three vertices inside of it?
2. Do you see a complete graph with two vertices inside of it?
3. Do you see a complete graph with one vertex inside of it?

Trees have two properties that graphs don't possess in general:

• They have a special point (vertex), called "root";
• They have no "circuits" -- no paths that lead off from a point and then arrive back eventually, as in the tetrahedron.

That means that there's a unique path between any two vertices (which is not true for tetrahedron, because there are circuits in that graph).

Each time we add a new point (vertex), we have to connect it to the other points (vertices): so how do the number of connections grow with the number of points? We want a formula:

\(arcs(n\ vertices) = ....\)

To get the answer, we start with a table, and try to figure out the pattern (remember, mathematicians are pattern lovers!).

\(K_n\) \(arcs(K_n)\) 1 0 2 1 3 3 4 6 5 ?

This problem is related to another story, about a little boy who became the greatest mathematician of all time.... Carl Friedrich Gauss ("the Prince of Mathematicians").

The story is told in a different way in one of your reading assignments (Rock Groups).

I want to think back to the number 6, and beer:

In terms of its personality, 6 is a triangular number: a number, like 55, which can be represented as a isoceles right triangle (above), or like these perfect stacks of balls:

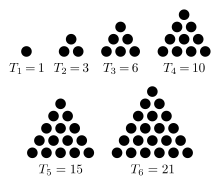
Numbers (like squares), which can be represented by some geometric figure are called polygonal numbers. Another interesting example given in Rock Groups, are the perfect squares: \(n^2\) can be thought of as the sum of the first \(n\) odd natural numbers:

\(1+3+5+7+9\)

\(=25\)

These mysterious properties are parts of the personalities of numbers. What's your favorite natural number's personality? If your favorite number is 36, then you're lucky: it's both square and triangular!