- You will have a quiz Thursday over our readings of "From fish to
Infinity" (and the accompanying Sesame Street video).
Just make sure that you do your reading for this week.
The prime factorization stuff will be part of next week's quiz.
- If you haven't yet filled out a 3x5 cards, please fill out the
card, indicating
- Name
- Hometown
- What is your calling? ("a calling has to do with one's larger purpose, personhood, deepest values, and the gift one wishes to give the world.... A calling is about the use one makes of a career." David Orr, Earth in Mind)
- What is your dream job?
- What is something special about you?
- We went over the syllabus, had brief introductions, and got some insight into the logo and project that you will be doing on your own.
- We resolved to be dogs, and not turkeys!
- Then we talked a little about numbers: some mysterious, some fear-provoking, some favorites of ours.
- I was able to read Oscar's mind, and see that he is especially fond of 6.
- Then we spent time trying to get a handle on the number 6: what
makes it tick? We watched a Sesame Street video, and noticed
how Humphrey broke it down using his voice, into a cadence:
fish, fish, fish
fish, fish, fish
How would Humphrey's method have worked had there been
- 20 penguins?
- 13 penguins?
These vocal cues leads us to your next readings: Rock (maybe acorns would be better!) Groups, and The Loneliest Numbers (a bit of a summary of primes).
Hearing this pattern might have allowed Ingrid to communicate the order to the kitchen, but she struggled with it.
So Ernie introduced them to counting! Which is a one-to-one correspondence between the "counting numbers" and the plates of fish. More on this today.
- We discovered that we could break 6 down into the product of 2 and
3, numbers which I called "primes". 6 is "composed" of primes,
and so is called "composite". We break numbers down as
products, and I introduced the idea of a "tree" to represent
this:
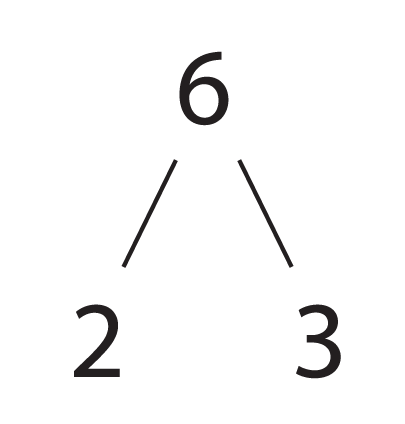
- When we discovered that seven is a problem but that six is not,
there was a guess -- a conjecture -- that it was the
fact that seven is odd that caused the trouble; that odd
numbers couldn't be decomposed.
We disproved the conjecture, by showing that nine is fine.
This is exactly how mathematics is done! A student generalized, based on the evidence, and proposed a rule, based on a pattern; sometimes the pattern will turn out to be true (although it wasn't in this case). So good work there....
The first few odds are indeed prime: 3, 5, 7 -- but 9 fails the pattern.
- At the end of class, I showed a clip from the documentary about Mathemalchemy, in which the artistic director Dominique describes how she has begun to appreciate the beauty of mathematics, and the camera panned over some chipmunks who are holding Babylonian (cuneiform) numbers, 12 and 13: one is composite, the other prime. Let's pick back up there!
Those chipmunks: what are they up to?
- First of all, they're playful chipmunks,
which is a key part of mathematics (which many of us
have forgotten).
They're playfully discovering the difference between prime and composite numbers.
The Chipmunks Sorting Primes Vignette explains a little more:

(Notice the title of the vignette: "Prime Play on a Prime Day: 3/11/43x47")
If we build a tree for 12, it will be in two steps: we need to do it, and then do it again! Let's see:
- So today we harken back to the primes along with those
chipmunks. Perhaps your favorite number is prime!
Definitions:
- The counting numbers are the positive integers: 1, 2, 3, .... These are also known as the natural numbers.
- A counting number is prime if and only if it has exactly two distinct divisors among the counting numbers: numbers 1 and itself.
- It is composite if and only if it has more than two distinct divisors among the counting numbers.
- Now what are those primes good for? We break numbers down using
primes as the building blocks, using trees to "expose" the
unique "prime factorization" of composite numbers.
Theorem (prime decomposition or prime factorization): every natural number (other than 1) is either prime, or can be written as a product of primes in a unique way, from smallest to largest.
Let's build some more "trees" for a few numbers, and talk about how we can associate a unique tree with a unique counting number (this is the key idea between one-to-oneness -- a perfect dance, with everyone matched up with just one partner).So 6 has a unique factorization (2*3 -- ordered from smallest to largest), and a unique tree (created by factoring the number -- in this case, 6 -- by primes, from smallest to largest). The root of the tree is the number itself, and the leaves of the tree dangle at the bottom of the prime factorization:

In the end, there's this notion: there is a one-to-one correspondence between counting numbers and their prime factorizations (with primes as their own partners), and their labelled trees (and the tree seems to summarize -- or contain -- the other two!):
6 $\iff$ 2*3 $\iff$ 
But the tree also contains an algorithm for finding the prime factorization, based on checking to see if factors of the given natural number can also be "decomposed".
Let's try another one: is 150 prime or composite?
- How are primes identified? Historically, the "Sieve of Eratosthenes" is the tool
that was used, and watch this
"animated solution", and watch for the spirals!
We found
- The only two adjacent primes,
- The triplet primes,
- The twin primes,
- "Spirals", and
- To test which numbers are prime, we need only test
those primes up to the square root of the number -- and no
larger. If by that point no prime divides the given number,
then the given number too is prime.
Here is a list of the primes less than 100:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 This list would allow you to test any number for primeness up to 10000 (because its square root is 100...).
Is 329 prime? It looks kind of primey...:) We only need to check primes up to 17, since \(\sqrt{329}\approx 18.14\), and the next prime is 19 which is greater than that.)
- So what about six? Strogatz in the article suggests that "...numbers are shortcuts for counting by ones...." (p. 5): so we might say that "six is a shortcut for counting by ones -- six times?"
- The key concept between the idea of number is the idea of
"one-to-one correspondence": a perfect matching.
Definition: a one-to-one correspondence is an association between two sets, so that each member of one set has a unique partner in the other set (and vice versa).It is the one-to-one correspondence between the fish and the numbers 1 through 6 (as shown in the video) that is the essense of "counting". It is dependent, of course, on the order of our numbers; that we present them in the proper order: 1, 2, 3, ....
- I ended with a preview of another way of thinking about the counting numbers, and we'll pick up there today.

A strange side-note:
The French defined the meter as one ten-millionth of the distance between the equator and the north pole on a great circle passing through Paris (makes perfect sense to me....:). So the government put official "meter sticks" around the city, so that anyone could check their measures (e.g. a piece of cloth) with this "official" meter.
In Paris there is still one of the "sticks" (it's marble!) "standing" (well, actually it's along a wall at a bus stop in Paris):

So should we create marble statues of six fingers being held up, with a sign saying "six"?
Perfect matching: we will indicate the number six with something that yells "Six" to everyone. You can bring up "six" candy bars, to see if you really have six -- by matching them to fingers of marble....
Or we could just count...:)
- One is the loneliest number, but that
- Two can be as bad as one; it's the loneliest number since the number one.
- I can prove that all counting numbers are interesting, using order!
Other numbers seem very gregarious; they play well with other numbers (e.g. 6, which seems particular friendly with 2 and 3; or 12, which has lots of friends: 2,3,4,6!).
But how can we understand "6" without understanding "5" as well? (and thus 4, 3, 2, 1,...0?) We'll discover that 0 was pretty hard to understand from early on!
Definition: a graph is a collection of points ("vertices") as well as a collection of arcs ("edges" -- each of which joins two points).
An edge can even join a vertex to itself, which is called a loop in a graph.

Definition: If every vertex in a graph is connected to every other (different) vertex by a single arc, we call it a complete graph.
Each number, considered as a complete graph, encompasses all the numbers that go before it:
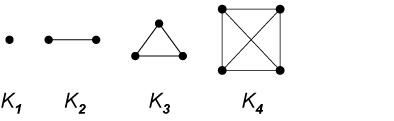
This picture of "four" (which is known as "\(K_4\)") has an unfortunate feature: its edges appear to overlap. We can alleviate the problem by pulling \(K_4\) out of the plane (two dimensions), and turning it into a three-dimensional animal (one of which I've brought with me today:
The tetrahedron (one of the Platonic solids, which we'll study down the road) is actually also the complete graph with four vertices:
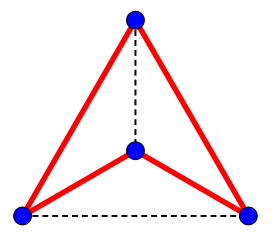
- Do you see the complete graph with three vertices inside of it?
- Do you see the complete graph with two vertices inside of it?
- Do you see the complete graph with one vertex inside of it?

Trees have two properties that graphs don't possess in general:
- They have a special point (vertex), called "root";
- They have no "circuits" -- no paths that lead off from a point and then arrive back eventually, as in the tetrahedron.
Each time we add a new point (vertex), we have to connect it to the other points (vertices): so how do the number of connections grow with the number of points? We want a formula:
\(arcs(n\ vertices) = ....\)
To get the answer, we start with a table, and try to figure out the pattern (remember, mathematicians are pattern lovers!).
|
 |
This problem is related to another story, about a little boy who became the greatest mathematician of all time.... Carl Friedrich Gauss ("the Prince of Mathematicians").
The story is told in a different way in one of your reading assignments for next time(The Loneliest Numbers).