Day 1, MAT115R

http://www.nku.edu/~longa/classes/mat115r

• For you to be successful, your attitude is as important as your ability.
• What you do shows what you are.
• Wherever you are, be all there. Jim Elliot

1. Name
2. Hometown
3. What is your calling? ("a calling has to do with one's larger purpose, personhood, deepest values, and the gift one wishes to give the world.... A calling is about the use one makes of a career." David Orr, Earth in Mind)
4. What is your dream job?
5. What is something special about you?
6. What's your favorite number? (And why, if you don't mind!)

You are encouraged to help me out if I misunderstand what your classmates say.

• Class will be organized around discussions of material, and activities. I hope that you will contribute! Chime in!

• I find that students are best at explaining ideas to other students. So what I shoot for is some students to get the idea in class, and then for them to "infect" the rest of the students. (No Covid, please, but infections of ideas are encouraged!:)

• This to not going to be a "practical math" course: you will not learn how to balance a checkbook.

  This is a course incorporating material for a broad range of liberal arts disciplines. Some of them will be interesting to you, some of them may not. But this is not another algebra course. You may never have seen any mathematics quite like the things that we're going to study in this course!

• Notice that you will have an evaluation of some sort every Thursday (including this Thursday!).
• The quiz will cover some or all of your homework (as well as the readings) from the current and previous week. It pays to do your homework, since you never know which homework problems will be selected for special attention!

I ask that you keep the phones out of sight. If, for some reason, you need to use your phone, please leave the classroom.

It's really distracting for me to see someone playing on their phone during class. And if I get too distracted, I absent-mindedly begin making your quizzes and tests a lot harder....:)

Did anyone see a giant sculpture (Mathemalchemy) when it was here last year, upstairs on the fourth floor near the center atrium?

If so, you have seen Mathemalchemy!

It was a huge effort (and $20K) to get it here, thanks to the generousity of our department, but it served as the centerpiece of this course last year. And the reason why is because

-- right where they belong!

1. Keep an open mind!
2. Just do it. Jump in. Make mistakes and fail, but never give up.
3. Often when we've done it once, we do it again, and again, and again.
4. Understand simple things deeply.
5. Look for patterns and similarities.
6. Break a difficult problem into easier ones.
7. Explore the consequences of new ideas. Generalize.
8. Examine questions from several points of view.
   Don't be a turkey -- be a dog! (this one may require a little explanation....) Can you think of three different ways to answer this question?

Numbers measure -- how much -- and they enumerate -- how many.

They quantify.

I'll need a couple of you to volunteer to have your minds read; who's up for it?

Does anyone here like Sesame Street? A fair number of people learned their first math at the knees of Big Bird (if he has knees!), and Bert and Ernie. So I like to start with a video from Sesame Street.

This video leads to a number of interesting questions:

• What exactly is six?
• Listen to Humphrey describe the order: what is he telling you about six by his voice?
• How would this performance differ had the room held seven fish-loving penguins?

In particular, we'll learn about the first (of three) important number decomposition, and I will introduce you to mathematical "trees".

Q: What do you suppose I mean by "decomposition"?

The artists who created Mathemalchemy used a wide assortment of artistic techniques to communicate mathematical ideas. Let's take a look at a snippet of a documentary featuring the artistic director, Dominique Ehrmann (part of your homework is to begin watching this video).

Hey, those chipmonks: what are they up to?

• First of all, they're playful, which is a key part of mathematics (which many of us have forgotten).

  They're playfully discovering the difference between prime and composite numbers.

  The Chipmunks Sorting Primes Vignette explains a little more:

  

  (Notice the title of the vignette: "Prime Play on a Prime Day: 3/11/43x47")

Definitions:

• The counting numbers are the positive integers: 1, 2, 3, .... These are also known as the natural numbers.
• A counting number is prime if and only if it has exactly two distinct divisors among the counting numbers: numbers 1 and itself.
• It is composite if and only if it has more than two distinct divisors among the counting numbers.

You might guess that Eratosthenes is a Greek mathematician, and you'd be right (actually born in Libya): but he was quite the scientist, too, and gave one of the first careful measurements of the Earth's diameter (even back around 200 BCE folks knew that the Earth was a ball. How would they know? Why would they suspect that?).

So 6 has a unique factorization (2*3 -- ordered from smallest to largest), and a unique tree (created by factoring the number -- in this case, 6 -- by primes, from smallest to largest). The root of the tree is the number itself, and the leaves of the tree dangle at the bottom of the prime factorization:

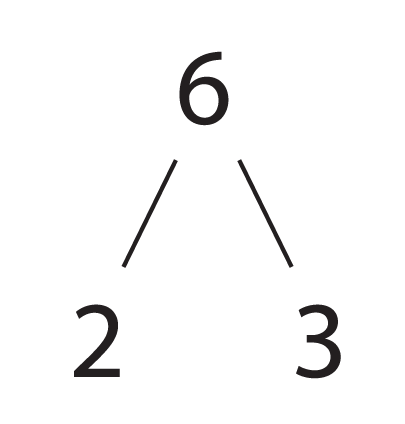
In the end, there's this notion: there is a one-to-one correspondence between counting numbers and their prime factorizations (with primes as their own partners), and their labelled trees (and the tree seems to summarize -- or contain -- the other two!):

6

$\iff$

2*3

$\iff$

But the tree also contains an algorithm for finding the prime factorization, based on checking to see if factors of the given natural number can also be "decomposed".

Let's try another one: is 150 prime or composite?