Day 6r, MAT115

• You have a quiz today over the Fraudini trick, binary factorization, primitive counting, and the reading. Also everything that we do in class last week! It might pay to review your agendas prior to quizzes, generally.

• For the quiz, you may have only hand-written notes (e.g. example problems, summaries of readings, etc.). If you have a calculator, great; if you must use your phone, then you may only use it in calculator mode, and it will be on the table in front of you.

• We looked at a few more properties of Pascal's triangle, including the sets of numbers that appear within them along the diagonals:
  • 0-dimensional ones, over and over again (1, 1, 1, 1, 1, 1, ....), which are stacked to make
  • 1-dimensional counting numbers (1, 2, 3, 4, 5, 6, 7, 8, ....), which are stacked to make
  • 2-dimensional triangular numbers (1, 3, 6, 10, 15, 21, 28, ....), which are stacked to make
  • 3-dimensional tetrahedral numbers (1, 4, 10, 20, 35, ....)
  This goes on, forever! We studied these numbers with pennies:
  

  The next numbers in the series have to be represented in 4 dimensions, and they're called the pentatopes:

  

  Much in Mathemalchemy was inspired by Dominique Ehrmann's textile, metal, and wood sculpture Time to Break Free. A two-dimensional traditional quilt breaks its chains and enters a time machine that will transform it into a three-dimensional form.

  Similarly, the figurate numbers are breaking their chains....

Today's Question of the Day:

• Well, not exactly up its sleeve, but how about this shawl? This illustrates the Sierpinski triangle, the fractal that we drew inside Pascal's triangle last time. (Here's a video of a student demonstrating this, along with some other interesting tidbits...)

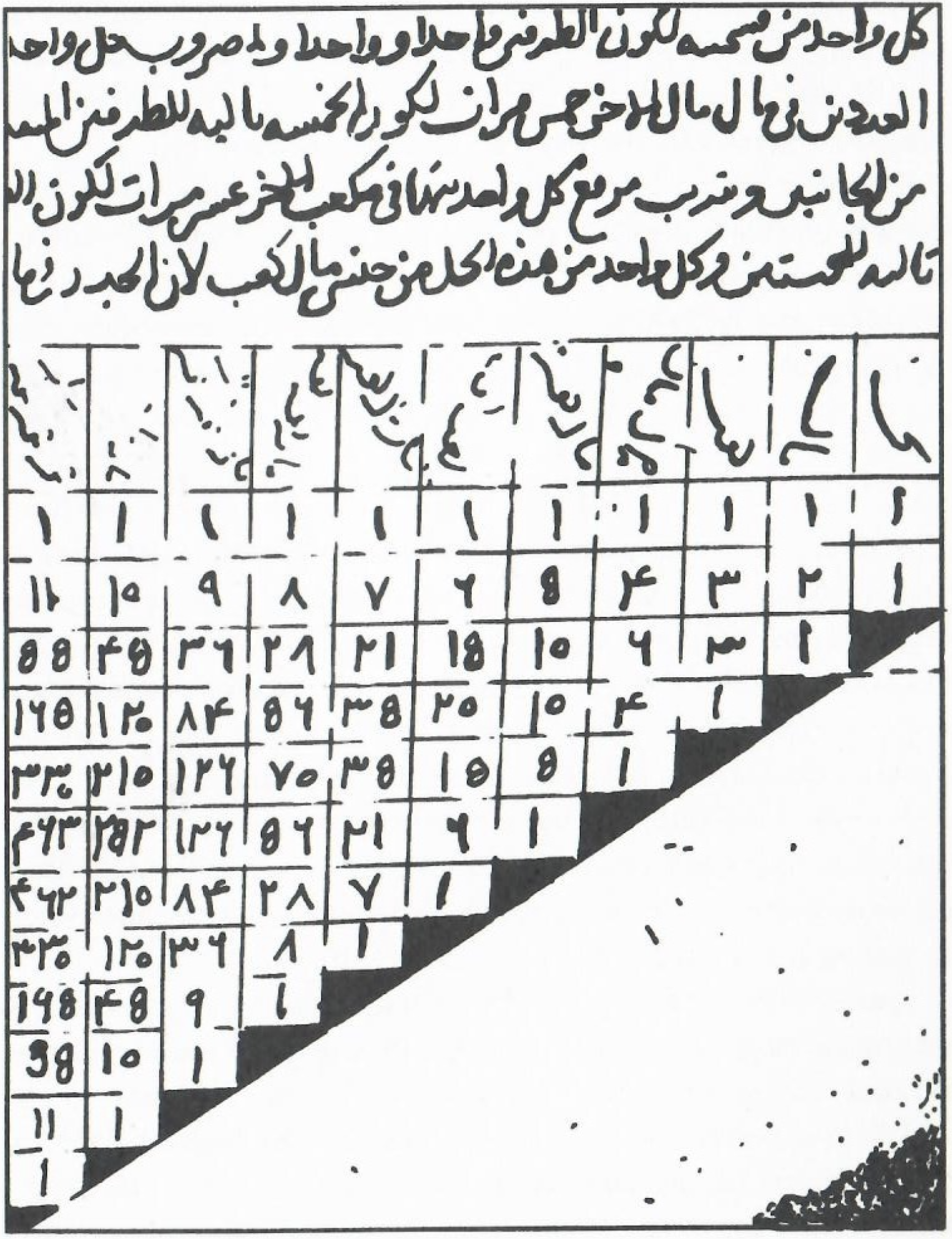
• This short reading (which I've asked you to read for homework) gives a third version of the triangle, from the Arab world, and a little background on the influence of Indian culture on our number systems.

  Let's take a look at that triangle:

  

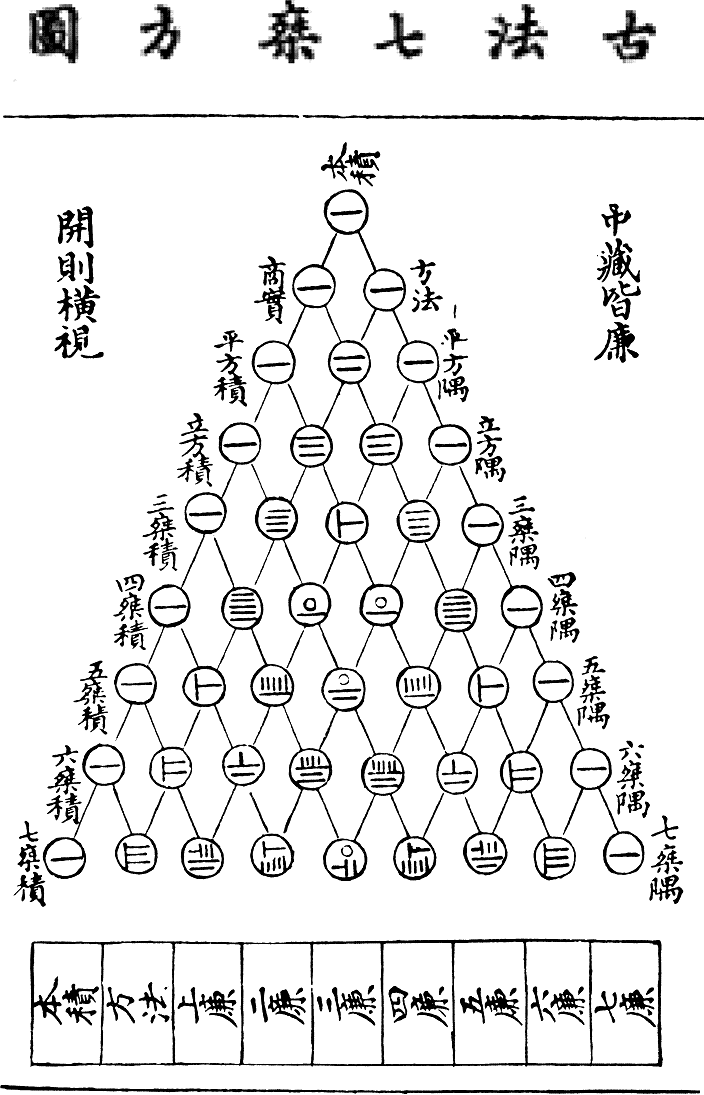
• Let's talk a little more about Yanghui's version, in particular the bamboo counting rods:
  

• Let's go back to different Facebook configurations again, and do some examples.

  1 individual 2 individuals 3 individuals, with two friendships? 4 individuals, with three friendships?

  Each choice of a different set of friendships results in a different Facebook. So we begin by asking how many arcs X are possible, and then asking how many ways can we pick Y arcs from X?

  How do we use Pascal's triangle to find the answer for a given number of people? We first find the number of arcs for the given number of people (the appropriate triangular number \(T\)), and then read off the number of different ways of having a given number of Facebook friendships from the "\(T\) row" of the table.

  ---

  So if there are 6 arcs (as there are for \(K_4\)), we look at the "6" row, and we can read off the number of ways of having 0, 1, 2, 3, 4, 5, and 6 friendships; and we can calculate probabilities of any particular type, if we were to select a type at random, by dividing by all the possible ways of selecting. This is given by the appropriate power of 2: \(2^6=64\) in this case since we're in the 6th row.

  ---

  The same process works if we want to decide questions like Pascal's about boys and girls, such as

  You have four extra tickets to a concert; in how many ways could you choose a set of four friends from your seven favorite friends? (Notice that it's the same number of ways as the number of ways of excluding three friends: the table is symmetric!)

• Pascal's triangle is useful for counting the ways of combining terms in the "algebraic expression" (called a "binomial")

  \[ (a+b)^n \]

  So, for example,

  \[ (a+b)^0=1 \] \[ (a+b)^1=1a+1b \] \[ (a+b)^2=1a^2+2ab+1b^2 \] \[ (a+b)^3=1a^3+3a^2b+3ab^2+1b^3 \] \[ (a+b)^4=1a^4+4a^3b+6a^2b^2+4ab^3+1b^4 \]

  (see your assigned reading).

  I hope that you noticed Pascal's triangle peeking out from the right hand sides above!

  Now we can see why the 11 powers work: \[ 11^0=(10+1)^0 = 1 \] \[ 11^1=(10+1)^1= 1*10 + 1*1 \] \[ 11^2=(10+1)^2=1*10^2+2*10*1 + 1^2 \] \[ 11^3=(10+1)^3=1*10^3+3*10^2*1+3*10*1^2 + 1^3 \] etc.!

• What this allows us to do is calculate the probabilities of more interesting situations.

  For example, the problem we did last time with the coin tosses. Since we're doing our experiment three times, we'll look in the 3 row: \[ (a+b)^3=1a^3+3a^2b+3ab^2+1b^3 \]

  If we think of \(a\) as the probability of a head, and \(b\) as the probability of a tail, and if it's a fair coin, so we set \(a=b=\frac{1}{2}\), then we get \[ (\frac{1}{2}+\frac{1}{2})^3=1\frac{1}{2}^3+3\frac{1}{2}^2\frac{1}{2}+3\frac{1}{2}\frac{1}{2}^2+1\frac{1}{2}^3 \]

  \[ 1 = \frac{1}{8}+\frac{3}{8}+\frac{3}{8}+\frac{1}{8} \] \[ 1 = P(\text{0 tails})+P(\text{1 tails})+P(\text{2 tails})+P(\text{3 tails}) \]

  For example, suppose that the probability that you have a cold on a given winter day is \(a=1/100\); then the probability that you don't have a cold is \(b=99/100\).

  Let's suppose that winter is 90 days long. What is the probability that you have a cold-free winter? We need to compute the 90th row in the table, which has some really big numbers!

  \[ \left(\frac{1}{100}+\frac{99}{100}\right)^{90} \]

  • Probability of a cold-free winter: \[ 1\left(\frac{1}{100}\right)^0 \left(\frac{99}{100}\right)^{90} \approx 0.4047 \]
  • Probability of a one-day cold winter: \[ 90\left(\frac{1}{100}\right)^1 \left(\frac{99}{100}\right)^{89} \approx 0.3679 \]
  • Probability of a two-day cold winter (uh oh, we need the rest of the 90th row of the triangle!:): \[ 4005\left(\frac{1}{100}\right)^2 \left(\frac{99}{100}\right)^{88} \approx 0.1654 \]
  • Probability of a three-day cold winter: \[ 117480\left(\frac{1}{100}\right)^3 \left(\frac{99}{100}\right)^{87} \approx 0.0490 \]
  • etc.

• Hexagonal Paper