Day 14r, MAT115

Last Time

Next Time

Announcements:
- Today's quiz covers symmetry, which we continue discussing today.
- I've assigned a short reading about symmetry.
- "In their recent books, Richard Prum and Michael Ryan synthesize research on animals and people, exploring possible evolutionary explanations for our own aesthetic tastes. Ryan is particularly interested in the innate sensitivities and biases of our neural architecture: He describes how our visual system, for example, may be wired to notice symmetry."
  How Beauty Is Making Scientists Rethink Evolution: The extravagant splendor of the animal kingdom can't be explained by natural selection alone -- so how did it come to be?
- Hermann Weyl has this to say in the concluding paragraph of his book Symmetry:
  "Symmetry is a vast subject, significant in art and nature. Mathematics lies at its root, and it would be hard to find a better one on which to demonstrate the working of the mathematical intellect."

Last time:

We discussed regular polygons, their use in tiling, etc.;

then moved into three-dimensional space to consider the Platonic solids: they're super-symmetric solids! Here they are again:

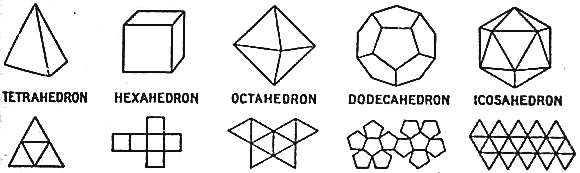
The Five Convex Regular Polyhedra (Platonic solids) -- thanks Wikipedia!
Tetrahedron	Hexahedron or Cube	Octahedron	Icosahedron	Dodecahedron
(Animation)	(Animation)	(Animation)	(Animation)	(Animation)
fire	earth	air	water	universe

We consolidated some information about Platonic solids in this table:

# of Vertices Edges Faces faces at each vertex sides at each face

Tetrahedron 4 6 4 3 3

Cube 8 12 6 3 4

Octahedron 6 12 8 4 3

Dodecahedron 20 30 12 3 5

Icosahedron 12 30 20 5 3

What conclusions can we draw from this data? Is there a pattern? (Of course there is!:) The pattern leads to the concept of "Duality":

Before we get back to the Platonics, any questions on the four page handout?
Today's Question of the Day:

What is this duality?
- Each Platonic solid has a "twin" -- called its dual -- which we can discover from the table.
Dualing examples:
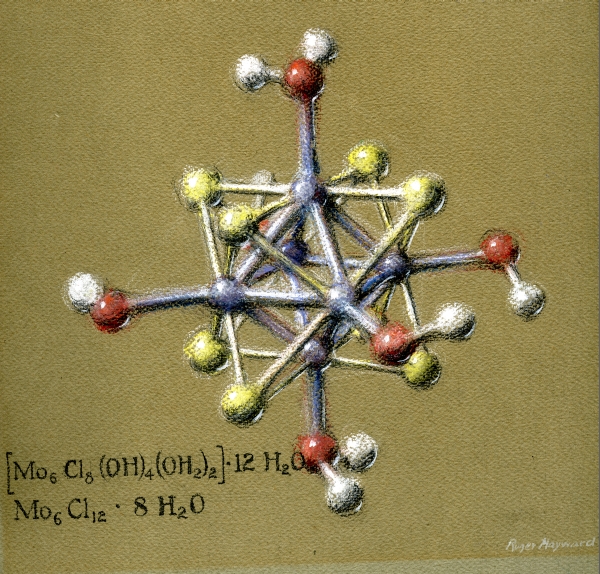
- Pastel drawing of a compound of Molybdenum Dichloride:
- Superconductivity:
- How can we draw the Platonic solids on a sheet of paper? We project them onto the paper.
  - The cube you've undoubtedly done before.
  - The tetrahedron can be drawn to be a "distorted" Mercedes symbol
  - Here are all the solids. Practice drawing them! Where's the duality?
Links:
- Symmetry, by Hermann Weyl (Princeton University Press, 1952)
- All wallpapers (there are 17 of them!)
- Symmetry Handout Key (annotated)
- Symmetry of lifeforms on Earth
- A fun reading on symmetry
- All wallpapers
- Hexagonal Paper

Website maintained by Andy Long. Comments appreciated.

Fibonacci's solution in Liber Abaci,, chapter 12:
Because the above written pair in the first month bore, you will double it; there will be two pairs in one month. One of these, namely the first, bears in the second montth, and thus there are in the second month 3 pairs; of these in one month two are pregnant and in the third month 2 pairs of rabbits are born, and thus there are 5 pairs in the month; ...
there will be 144 pairs in this [the tenth] month; to these are added again the 89 pairs that are born in the eleventh month; there will be 233 pairs in this month.
To these are still added the 144 pairs that are born in the last month; there will be 377 pairs, and this many pairs are produced from the abovewritten pair in the mentioned place at the end of the one year.
You can indeed see in the margin how we operated, namely that we added the first number to the second, namely the 1 to the 2, and the second to the third, and the third to the fourth and the fourth to the fifth, and thus one after another until we added the tenth to the eleventh, namely the 144 to the 233, and we had the abovewritten sum of rabbits, namely 377, and thus you can in order find it for an unending number of months.

	# of Vertices	Edges	Faces	faces at each vertex	sides at each face
Tetrahedron	4	6	4	3	3
Cube	8	12	6	3	4
Octahedron	6	12	8	4	3
Dodecahedron	20	30	12	3	5
Icosahedron	12	30	20	5	3