Day 16, MAT115R

• The quiz
• Key

You should be able to write our numbers in either system, and translate their numbers into our own.

• We interpreted a few Mayan numbers in the calendar, enough to learn that they had a character for zero (a cowry shell, perhaps).

• We wrote these numbers in Mayan:
  1. 47
  2. 400
  3. 573
  4. 3600
  5. 7200
  6. 14001

Rules:

• There are two players, Player 1 and Player 2.
• An arbitrary number of counters is thrown down (e.g. toothpicks, pennies).
• Objective: The player who picks up the final counter wins.
• Player 1 will go first. On the first play, Player 1 must pick up at least one counter, but may not pick up all the counters (otherwise this would be a silly game!).
• Player 2 must then pick up at least one counter, and not more than twice the number of counters picked up on Player 1's turn.
• The players then alternate turns, subject to these same conditions: pick up at least one, no more than twice what the preceding player took.
• The player who legally picks up the final counter on their turn wins.

But, in spite of all these advantages, she failed to beat me at Fraudini Nim.

"A certain man had one pair of rabbits together in a certain enclosed place, and one wishes to know how many are created from the pair in one year when it is the nature of them in a single month to bear another pair, and in the second month those born to bear also." (source).

(Oh no! A story problem! Here's Fibonacci's solution.)

But I prefer a tree:

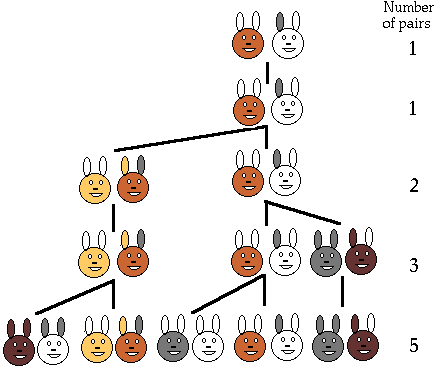
Notice that we're counting pairs, not individual rabbits....

The first few Fibonacci numbers (those below 100):

It says that the population at the \(n^{th}\) moment is the sum of the population at the previous month plus the population at the month before that. Here's why that makes sense:

• Because the pairs are immortal, every pair that was present in the previous month will still be present at the current month.
• And because every pair that was present two months ago is macture enough to produce a new pair of rabbits, this population contributes the new (baby) pairs.

• Rules for "Fraudini Nim":
  • There are two players, Player 1 and Player 2.
  • An arbitrary number of counters is thrown down (e.g. toothpicks, candies, pennies).
  • Objective: The player who picks up the final counter wins.
  • Player 1 will go first. On the first play, Player 1 must pick up at least one counter, but may not pick up all the counters (otherwise this would be a silly game!).
  • Player 2 must then pick up at least one counter, and not more than twice the number of counters picked up on Player 1's turn.
  • The players then alternate turns, subject to these same conditions: pick up at least one, no more than twice what the preceding player took.
  • The player who legally picks up the final counter on their turn wins.

• Okay, so what's the strategy? How does one win at Nim? How could I be so confident that I was going to beat anyone?

  We tried to figure out the strategy, by creeping up on it. When you confront a big problem, start with some really simple examples.

  • We looked at some of the simplest cases, and this is what we concluded:

    Number of counters	1	2	3	4	5	6	7	8
    Winner (1 or 2? -- if they play right!)	X	P2	P2	P1	P2	P1	P1	P2

  • The first few Fibonacci numbers (those below 1000): 1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,....

  • What's the winning strategy in Fraudini Nim? It all hinges on this, the third of our big factorizations:

    The Fibonacci factorization

    ---

    Every natural number is either

    1. Fibonacci, or
    2. it can be written as a sum of non-consecutive Fibonacci numbers in a unique way.

    ---

    Examples?

    1. 89 is Fibonacci
    2. 28 = 21 + 7
    3. 67 = 55 + 8 + 3 + 1
    Warning: don't try to break up Fibonacci numbers! Once you've hit a Fibonacci, you stop. So, for example, don't try to break up the 8 in the sum \(67 = 55 + 8 + 3 + 1\)

  • Now, for the secrets of Fibonacci Nim. You need to learn this strategy, and you can't lose.

    Suppose there are $n$ counters on the table to start.

    1. First or Second? To be "in the driver's seat", you should
       • arrange to go second only if $n$ is Fibonacci;
       • go first otherwise.

    2. Your move? If you're in the driver's seat, then you'll be able to do this:
       • First of all, if you can legally take all the counters, do so! Then you win. Otherwise,
       • Write $n$ as the unique sum of non-consecutive Fibonacci numbers; call the smallest Fibonacci in the sum $m$.
       • Take $m$ counters.
       You'll be guaranteed a victory.
       You'll know that you're not in the driver's seat if you can't follow this strategy. The reason why? Remember that you can only take up to twice what your opponent took. Although you might write the number of counters remaining as a sum of Fibonacci numbers, you will find that you are not allowed to take even the smallest of the Fibonaccis -- it will be more than twice what your opponent picked up, so that would be illegal.
    Let's look at some examples:

    • 29 counters, and you're first. You're in the driver's seat, since 29 isn't Fibonacci.

      29 = 21 + 8

      so you take 8.

      I, player two, am up, and I am looking at 21. It's already Fibonacci. I can't take the smallest in the "sum" -- 21. So I'm out of luck. I can't follow "the strategy". Whatever I take, you'll be able to beat me.

      To slow things down, I take 1.

      It's now 20 to you. 20 = 13 + 5 + 2. So you take 2 (that's legal). And so on, and you're going to beat me. Argh!

    • 34 counters, and you're second. You're in the driver's seat, since 34 is Fibonacci.

      Suppose I go first, and take 4.

      Then it's 30 to you. 30 = 21 + 8 + 1, so you take 1. Now it's 29 to me.

      You might think "29 to Long, and he can pick first -- he's going to win!" But that's wrong. I'd like to take 8, as before, but I can't -- because 8 is more than twice what you took.

      So I'm stuck -- and you're on track to win my money!

    Now here's another key point: when you're not in the driver's seat, take 1 -- the smallest legal move. That's because you want to slow down the game, and let your opponent make a mistake and put you back in the driver's seat.

  • So basically, the whole things comes down to this. If you can choose whether to go first or second, do it based on whether the number is Fibonacci or not and you're guaranteed a victory (as long as you don't make any mistakes...).
    1. Go first for non-Fibonacci, second for Fibonacci.

    2. Of course, take all of the counters if that's a legal move.

    3. Whatever the number of counters on the table, write it as its unique sum of non-consecutive Fibonacci numbers;
       1. take the smallest Fibonacci, if you can; you're now in the driver's seat, and should win.
       2. if you can't take the smallest (because it's more than twice your opponent's move), take 1 -- it will slow the game down, and hopefully your opponent will make a mistake.

Watch Dave Brubeck's leg, counting out the rhythm....