- Today's quiz will be over golden stuff, and spirals.
- Today is the judging for the "Art Show of Spirals". Please vote
for your favorite three (but not your own); so put your name on your
ballot. Results will be anonymous, nonetheless.
These are our entries!
I'll show each for about 10 seconds, then we'll go back through briefly so that you can gaze at each one one more time before you make your choice.
Each image has a number next to it -- make sure that you include that (but you can also give a brief description or some kind word to explain why you liked it).
- You also have a fairly lengthy homework assignment, so
please get started on it.
It will form the basis of our quiz, with some of my favorites from the first day of Symmetry also coming in....
- Thanks to Evan for a couple of links:
- Fetuses
May Respond to Faces While in the Womb: Babies develop a
preference for face-like light patterns even before birth
Remember these creepy faces? Seems like kids gravitate to the more face-like one even in the womb!
- Giotto and the Perfect Circle
- Fetuses
May Respond to Faces While in the Womb: Babies develop a
preference for face-like light patterns even before birth
- I lied about building the 3-D models of the Platonic solids today: we'll do it our first day back from break, I promise!
- We worked on
our four-page
homework, which explores reflective and rotational
symmetries of two-dimensional figures.
We basically looked at an example or two of each type of problem. Any questions on those?
- Because of today's quiz, I want to share a little exercise that
combines primes and spirals.
I want to talk about an ancient algorithm (the "Euclidean algorithm") for finding the greatest common divisor of two counting numbers.
It turns out that successive Fibonacci numbers are the algorithm's "worst case scenario" for finding the GCD (greatest common divisor) of two numbers. We will investigate that with this handout.
For example what is the GCD of 39 and 15? What is the largest counting number that divides both evenly?
Let's see how Euclid would find the answer, algebraically and then using geometry.
Then we'll try a few more examples:
- gcd(40,24)
- gcd(40,7)
- gcd(34,21)
Today we consider the Platonic solids, which possess a great deal of symmetry: they're super-symmetric solids.
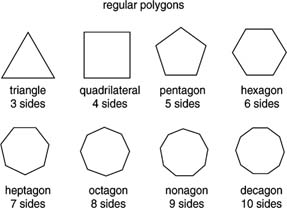
- We begin our discussion with the convex regular
polygons:
"A regular polygon is a polygon which is equiangular (all angles are equal in measure) and equilateral (all sides have the same length). Regular polygons may be convex or star."
- In a previous class we mentioned regular convex hexagonal
graph paper, which represents a tiling of the plane by a
regular convex polygon. You may have seen these kinds of tilings in bathrooms.
Bees have the same idea:
- The honeycomb is actually solid -- three-dimensional. The tubes
have hexagonal walls. But the comb is not Platonic.
A cube is an example of a Platonic solid. It's the one we're most familiar with, so let's start with that.
A Platonic solid is a solid for which
- All faces are congruent (identical) convex regular polygons, and
- Each face, each edge, and each vertex is exactly equivalent to every other face, edge, or vertex (respectively).
They're super-symmetric!
The Five Convex Regular Polyhedra (Platonic solids) -- thanks Wikipedia! Tetrahedron Hexahedron
or CubeOctahedron Icosahedron Dodecahedron 
fire earth air water universe - What do these have to do with Plato? According to Weyl, "Plato, in the
dialogue Timaeus, associates the regular pyramid, octahedron,
cube, icosahedron, with the four elements of fire, air, earth and water
(in this order), while in the pentagondodecahedron he sees in some sense
the image of the universe as a whole."
- As a "homework" (for your own good!), I am asking you to cut and
create Platonic solids out of paper, using this template. You
may use these as a cheat sheet for the next exam. You must have put
them together, however, and you must use only your own.
- What's wrong with six sided polygons, and beyond? Consider the
hexagonal graph paper, of the tiling of the plane: why can't it be folded up
into a solid?
The answer involves Euler's formula, as Weyl discusses.
- What can you do with these solids?
- Play basketball? Three Sides to This Story: Knicks Dust Off
Phil Jackson's Triangle Offense, from the New York Times:
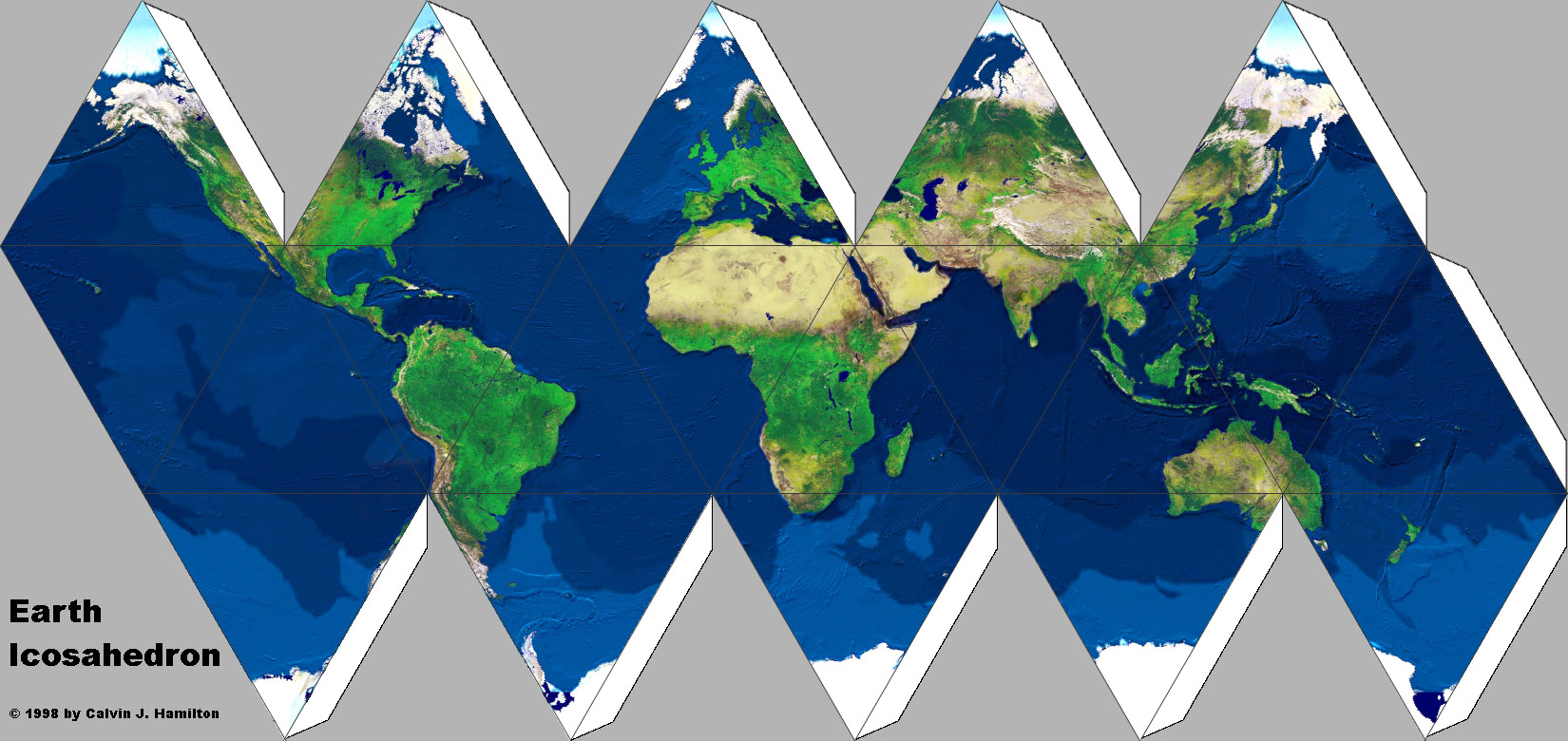
- Map the Earth?
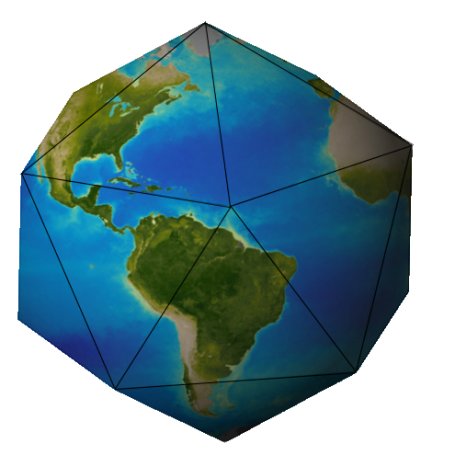
The Platonic solids allow us to make "flat spheres" (sort of!):
- Johannes Kepler thought that the orbits of the planets (of which
five were known at the time) were somehow related to the various
Platonic solids, as shown in
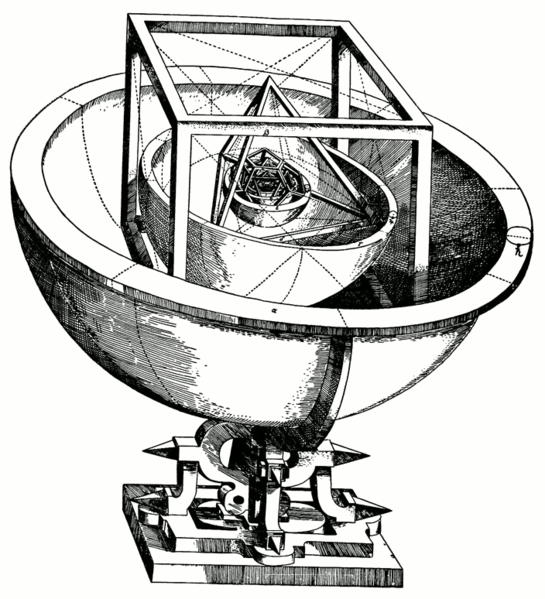
"The six spheres each corresponded to one of the planets (Mercury, Venus, Earth, Mars, Jupiter, and Saturn). The solids were ordered with the innermost being the octahedron, followed by the icosahedron, dodecahedron, tetrahedron, and finally the cube. In this way the structure of the solar system and the distance relationships between the planets was dictated by the Platonic solids."
And then Uranus was discovered, and there was not a sixth Platonic solid. And so science evolves....
- Chemists know how important the Platonic solids are: here are some
great images from Linus Pauling's and Roger
Hayward's The Architecture of Molecules (a book created
especially for young people, and based off of Pauling's
article in the 1964 Proceedings of the National Academy of
Sciences.
From Pauling's paper:
Molecular architecture may be said to have originated in 1874, when J. H. van't Hoff and J. A. le Bel independently formulated the brilliant postulate that the four valence bonds of the carbon atom are directed approximately toward the corners of a regular tetrahedron. It was extended into inorganic chemistry in 1893, when A. Werner suggested that in many inorganic complexes six atoms are arranged at the corners of a regular octahedron about a central atom, and that other geometrical structures are represented by other complexes.These are some higher quality images than my scans:
- Beautiful pictures, such as this one of tantalumhalide
- More Beautiful pictures!
- So what can you do with a dodecahedron?
- Make a calendar!
- So what can you do with an icosahedron?
- Look like a super-brainy, cool scientist!
From the October 7th, 2011 New York Times
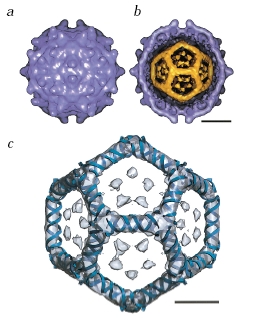
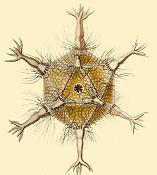
- Amoeboid protozoa Circogonia icosahedra:
- Viruses:
- The Cliff Notes Version...
"An array of viruses. (a) The helical virus of rabies. (b) The segmented helical virus of influenza. (c) A bacteriophage with an icosahedral head and helical tail. (d) An enveloped icosahedral herpes simplex virus. (e) The unenveloped polio virus. (f) The icosahedral human immunodeficiency virus with spikes on its envelope."
- The Cliff Notes Version...
- Dodecahedral
- Viruses:
- Viruses:
- Look like a super-brainy, cool scientist!
- More critters:
- Play basketball? Three Sides to This Story: Knicks Dust Off
Phil Jackson's Triangle Offense, from the New York Times:
- Now let's use what we can deduce of Platonic solids to fill in the
following table:
# of Vertices Edges Faces faces at each vertex sides at each face Tetrahedron Cube Octahedron Dodecahedron Icosahedron What conclusions can we draw from this data? Is there a pattern? (Of course there is!:) The pattern leads to the concept of "Duality":
- Each Platonic solid has a "twin" -- called its dual -- which we can discover from the table.
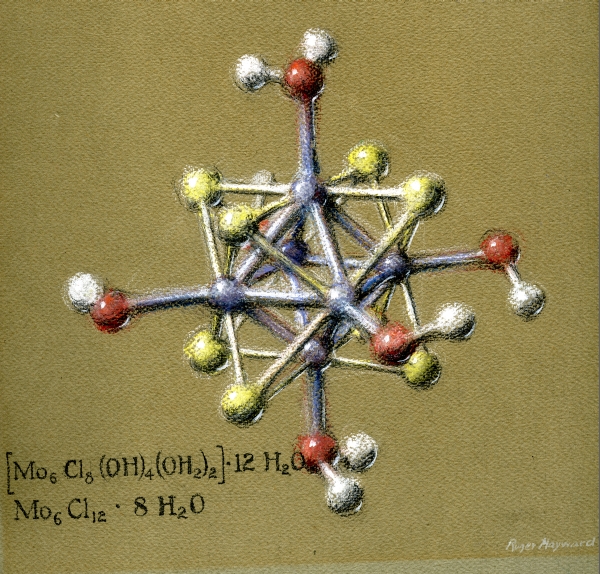
Pastel drawing of a compound of Molybdenum Dichloride:
- Each Platonic solid has a "twin" -- called its dual -- which we can discover from the table.
- Symmetry, by Hermann Weyl (Princeton University Press, 1952)
- Symmetry of lifeforms on Earth
- A fun reading on symmetry
- Meet the world's Mrs Averages: Scientists blend thousands of faces together to reveal what the typical woman's face looks like in 41 different countries from around the globe
- Comparing
theory--driven and data-driven attractiveness models using images of
real women's faces
This paper contains a lot of references, and on-line resources to document their work.
- The Brain's
Face Recognition System Is Easy to Fool:
The human brain is good at identifying faces, but illusions can fool our "face sense"
"Because the human brain is so good at detecting faces, we sometimes see them where they do not exist. Were you ever scared as a child by strange faces popping up from an abstract wallpaper design or formed by shadows in the semidarkness of your bedroom? Ever notice that cars seem to have faces, with the headlights as eyes and the grilles as mouths? These effects result from the face-recognition circuits of our brains, which are constantly trying to find a face in the crowd."
- Modeling individual preferences reveals that face beauty is not universally perceived across cultures
- Symmetry, by Hermann Weyl (Princeton University Press, 1952)
- Symmetry of lifeforms on Earth
- A fun reading on symmetry
- Hexagonal Paper
