Day 24, MAT115R

Last Time

Next Time

Announcements:
- Welcome back! I hope that it was a lovely break for each of you.
- Quiz results
  - The quiz was quite rough. Let's have a look....
- The "Art Show of Spirals" winners! The following all receive a GOQF card (which means I drop an additional low quiz grade.
  1. Evan -- 9 votes!
    Curiously, Evan's entry is not particularly golden: side ratios 1.47. How did you manage that Evan?
    Note that Evan's main image is not square....
  2. Finley -- 7 votes!
  3. And a tie for third: Brooklyn and Grace.
  4. Our bonus winners were Beth, Bela, and Amalie
  Nice work all! A very worthy collection of spirals.
Last time:
- Because of the impending quiz, I wanted to share a little exercise that combines primes and spirals.
  We talked about an ancient algorithm (the "Euclidean algorithm") for finding the greatest common divisor of two counting numbers.
  It turns out that successive Fibonacci numbers are the algorithm's "worst case scenario" for finding the GCD (greatest common divisor) of two numbers. We investigated that with a handout, and saw how the Fibonacci spiral was the result of going as slowly as possible down to a one-by-one square.
  Unfortunately, however, the exercise did not seem to inspire folks to make more beautiful Fibonacci spirals.....
  Fibonacci spirals require Fibonacci numbers for the side-lengths of the squares that we attach at each step.
  And so at each step we create another Fibonacci approximation to the golden rectangle, with side lengths the ratio of two successive Fibonacci numbers.

Today's Question of the Day:

Which of the Platonic solids are solid?

Today we construct the Platonic solids with GeoMags. These solids possess a great deal of symmetry: they're super-symmetric solids!

We will also finally fill out that table about the Platonic solids that's been floating around on the agendas for the past few times....

Platonic solid is a solid for which

All faces are congruent (identical) convex regular polygons, and
Each face, each edge, and each vertex is exactly equivalent to every other face, edge, or vertex (respectively).

They're super-symmetric!

The Five Convex Regular Polyhedra (Platonic solids) -- thanks Wikipedia!
Tetrahedron	Hexahedron or Cube	Octahedron	Icosahedron	Dodecahedron
(Animation)	(Animation)	(Animation)	(Animation)	(Animation)
fire	earth	air	water	universe

As a "homework" (for your own good!), I am asking you to cut and create Platonic solids out of paper, using this template. You may use these as a cheat sheet for the next exam. You must have put them together, however, and you must use only your own.
So we can build the Platonic solids in paper. But we can also build them with magnets!
What's wrong with six sided polygons, and beyond? Consider the hexagonal graph paper, of the tiling of the plane: why can't it be folded up into a solid?
The answer involves Euler's formula, as Weyl discusses.
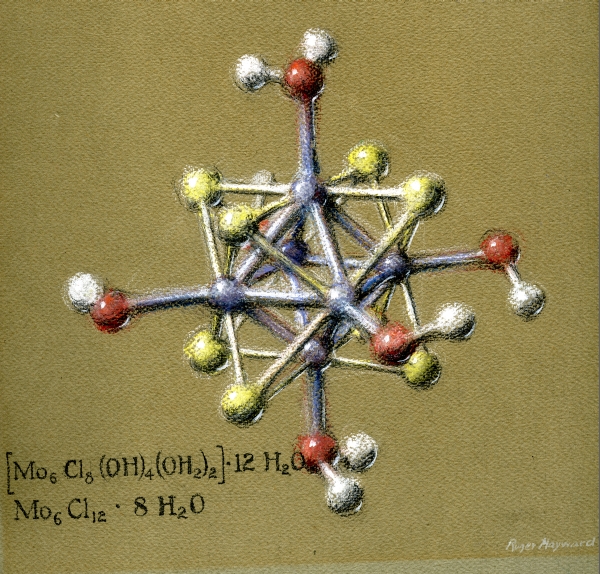
Chemists know how important the Platonic solids are: here are some great images from Linus Pauling's and Roger Hayward's The Architecture of Molecules (a book created especially for young people, and based off of Pauling's article in the 1964 Proceedings of the National Academy of Sciences.
From Pauling's paper:
Molecular architecture may be said to have originated in 1874, when J. H. van't Hoff and J. A. le Bel independently formulated the brilliant postulate that the four valence bonds of the carbon atom are directed approximately toward the corners of a regular tetrahedron. It was extended into inorganic chemistry in 1893, when A. Werner suggested that in many inorganic complexes six atoms are arranged at the corners of a regular octahedron about a central atom, and that other geometrical structures are represented by other complexes.
These are some higher quality images than my scans:
- Beautiful pictures, such as this one of tantalumhalide
- More Beautiful pictures!
So what can you do with a dodecahedron?
- Make a calendar!
So what can you do with an icosahedron?
- Look like a super-brainy, cool scientist!
  From the October 7th, 2011 New York Times
- Amoeboid protozoa Circogonia icosahedra:
  
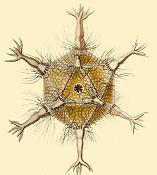
  (They also come in octahedra! Here's Circopurus octahedrus:
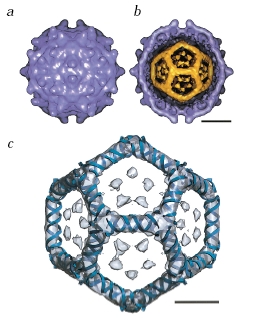
- Viruses:
  - The Cliff Notes Version...
    
    "An array of viruses. (a) The helical virus of rabies. (b) The segmented helical virus of influenza. (c) A bacteriophage with an icosahedral head and helical tail. (d) An enveloped icosahedral herpes simplex virus. (e) The unenveloped polio virus. (f) The icosahedral human immunodeficiency virus with spikes on its envelope."
- Dodecahedral
  - Viruses:
    
    "The structure of Pariacoto virus reveals a dodecahedral cage of duplex RNA"
More critters:
- Canine Parvovirus
- Enterobacteria Phage

Now let's use what we can deduce of Platonic solids to fill in the following table, while making examples with GeoMags:

# of Vertices Edges Faces faces at each vertex sides at each face

Tetrahedron

Cube

Octahedron

Dodecahedron

Icosahedron

What conclusions can we draw from this data? Is there a pattern? (Of course there is!:) The pattern leads to the concept of "Duality":

Each Platonic solid has a "twin" -- called its dual -- which we can discover from the table.

Pastel drawing of a compound of Molybdenum Dichloride:

Links:

Symmetry, by Hermann Weyl (Princeton University Press, 1952)
Symmetry of lifeforms on Earth
A fun reading on symmetry
Meet the world's Mrs Averages: Scientists blend thousands of faces together to reveal what the typical woman's face looks like in 41 different countries from around the globe
Comparing theory--driven and data-driven attractiveness models using images of real women's faces
This paper contains a lot of references, and on-line resources to document their work.
The Brain's Face Recognition System Is Easy to Fool: The human brain is good at identifying faces, but illusions can fool our "face sense"
"Because the human brain is so good at detecting faces, we sometimes see them where they do not exist. Were you ever scared as a child by strange faces popping up from an abstract wallpaper design or formed by shadows in the semidarkness of your bedroom? Ever notice that cars seem to have faces, with the headlights as eyes and the grilles as mouths? These effects result from the face-recognition circuits of our brains, which are constantly trying to find a face in the crowd."
Modeling individual preferences reveals that face beauty is not universally perceived across cultures
Symmetry, by Hermann Weyl (Princeton University Press, 1952)
Symmetry of lifeforms on Earth
A fun reading on symmetry
Hexagonal Paper

Website maintained by Andy Long . Comments appreciated.

Fibonacci's solution in Liber Abaci,, chapter 12:
Because the above written pair in the first month bore, you will double it; there will be two pairs in one month. One of these, namely the first, bears in the second montth, and thus there are in the second month 3 pairs; of these in one month two are pregnant and in the third month 2 pairs of rabbits are born, and thus there are 5 pairs in the month; ...
there will be 144 pairs in this [the tenth] month; to these are added again the 89 pairs that are born in the eleventh month; there will be 233 pairs in this month.
To these are still added the 144 pairs that are born in the last month; there will be 377 pairs, and this many pairs are produced from the abovewritten pair in the mentioned place at the end of the one year.
You can indeed see in the margin how we operated, namely that we added the first number to the second, namely the 1 to the 2, and the second to the third, and the third to the fourth and the fourth to the fifth, and thus one after another until we added the tenth to the eleventh, namely the 144 to the 233, and we had the abovewritten sum of rabbits, namely 377, and thus you can in order find it for an unending number of months.

	# of Vertices	Edges	Faces	faces at each vertex	sides at each face
Tetrahedron
Cube
Octahedron
Dodecahedron
Icosahedron