Day 25, MAT115R

• I made an assumption that you would complete your two projects well -- so please do.
• I used your first exam grade to predict your grades on your future exams as well. If your grade on that exam was low, hopefully you'll do better going forward!
• I used only one of your two drops for the quizzes (unless you have extra "GOQF" cards, which I applied right away).

• A Platonic solid is a solid for which
  • All faces are congruent (identical) convex regular polygons, and
  • Each face, each edge, and each vertex is exactly equivalent to every other face, edge, or vertex (respectively).

  They're super-symmetric!

  The Five Convex Regular Polyhedra (Platonic solids) -- thanks Wikipedia!
  Tetrahedron	Hexahedron or Cube	Octahedron	Icosahedron	Dodecahedron
  (Animation)	(Animation)	(Animation)	(Animation)	(Animation)
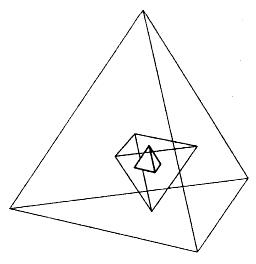
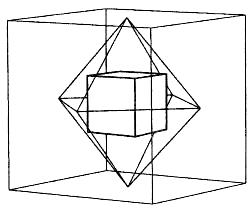
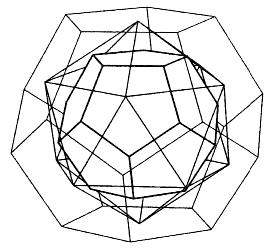
  fire	earth	air	water	universe

  The summary table, illustrating the duality between pairs of the solids (the tetrahedron is paired with itself!):

  Solid name	# of Vertices	Edges	Faces	faces at each vertex	edges at each face
  Tetrahedron	4	6	4	3	3
  Cube	8	12	6	3	4
  Octahedron	6	12	8	4	3
  Dodecahedron	20	30	12	3	5
  Icosahedron	12	30	20	5	3

  What conclusions can we draw from this data? Is there a pattern? (Of course there is!:) The pattern leads to the concept of "Duality":

  Each Platonic solid has a "twin" -- called its dual -- which we can discover from the table.

  "In the Hindu tradition, the icosahedron represents purusha, the male, spiritual principle, and generates the dodecahedron, representing prakriti, the female, material principle."

• The cube you've undoubtedly done before.
• The tetrahedron can be drawn as a Mercedes Benz symbol
• Here are all the solids, projected onto paper (from three dimensions down to two dimensions). Practice drawing them!

  It turns out that they can all be drawn without any edges intersecting each other. This is one of the important concepts we want to talk about today.

• The Bridges of Konigsberg problem: "is it possible to set off and walk around Konigsberg crossing each bridge exactly once?"

  What do you think?

  
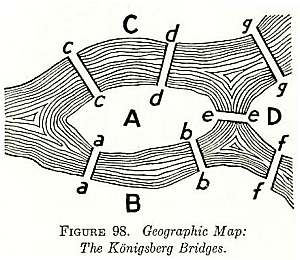
  • This problem, solved by Leonhard Euler (1735), was the beginning of graph theory.

    As a reminder, we'll review some of the definitions of graphs we've seen to this point, as well as get some new definitions.

    • Graphs are made up of vertices (points) and edges that connect the vertices. More formally, a graph is defined as
      1. A collection of points, called vertices.
      2. A collection of edges, each of which connects two vertices (if the same vertex is used twice, the edge is called a loop).
      3. a rule telling how each edge is connected to a pair of vertices.

    • A graph is simple if it doesn't have any loops (edges connected from a vertix to itself), or multiple edges connecting the same two vertices.

    • Complete graphs are simple graphs with single edges between every pair of vertices (but no loops).

    • A graph is connected if there is a path (a means of moving from one vertex to another along edges) from each vertex to every other vertex.

    • The degree of a vertex is the number of edges coming into it.

  • Euler's solution:
    • Extract out only the important information into a graph (which, to that point, hadn't been invented!).
    • Konigsberg: To be traversable (i.e. have an "Euler path"), there must be at most two vertices of odd degree.
    • Euler noticed the hand-shaking theorem: in any graph, the number of vertices with odd degree must be even.
    • An alternative solution.
    • "Floor plans" of houses either have an Euler path, or they don't. The rooms are like land masses, and the doors are like bridges. Let's try one!

• Graphs don't change by bending edges, but breaking them or detaching edges from their vertices (and hence creating new vertices) gives new graphs.

• Exercises: on simple graphs
  • Draw all the distinctly different simple graphs with three vertices.
    • A cycle is a route from a node back to itself that doesn't retrace steps.
    • One of these graphs is a (non-rooted) tree: a connected graph that has no cycles.
      • Where have we seen trees used before?:)
    • Duality -- again!
  • Draw all the distinctly different simple graphs with four vertices.
    • Have you ever seen any of these before? Could we give any of them names?
    • Sometimes it's hard to tell if two graphs are actually the same... We say "isomorphic".
    • Can you draw them in a way that emphasizes symmetry?
    • Can you draw them in a way that emphasizes duality?

• Planar graphs are graphs that can be drawn such that no two edges intersect.
  • Every Platonic graph can be drawn this way, so they are planar graphs.

  • As a "homework" (for your own good!), I have asked you to cut out and create Platonic solids from paper, using this template.

    Let's inspect these drawings, and see why these five configurations of polygons work: while two of these polygons can tile the plane (the square and the triangle), we throw out enough neighbors of each of the polygons so that there's room to fold up the cut-outs.

    The pentagon won't tile the plane -- there must be space between some pentagons. Any polygon with more than five sides will be "too cramped" to fold up....

    Note: these are not graphs of the Platonic solids, because many of the "edges" are redundant, and there are too many vertices.

  • Euler also discovered a formula for planar graphs: \[ F-E+V=2 \] where F is the number of faces, E the number of edges, and V the number of vertices.

    If we check our table for the Platonic solids, we'll see that they all hold up.

    It turns out that it also works for soccer balls, and other polyhedra. The countries on a globe, for example. Actually anything that can be projected onto planar graph!

    Euler's formula is also what's wrong with six-sided polyhedra (and beyond).

    The argument against six-sided polyhedra involves Euler's formula, as Weyl discusses.

  • Which of the Platonic solid graphs can be traversed without backtracking?

• Exercises:
  • We can show that the complete graph with four vertices is planar.
  • Let's see if we can show that the complete graph with five vertices is not planar:

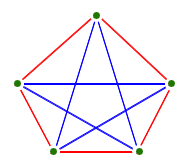
    Why not? What goes wrong?

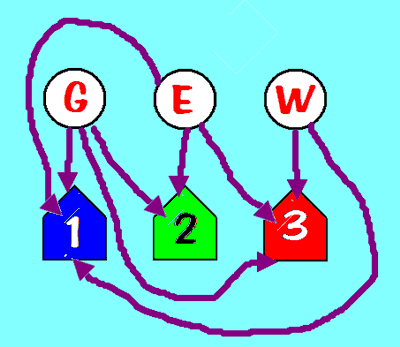
  • The three utilities and three houses graph is not planar:
    

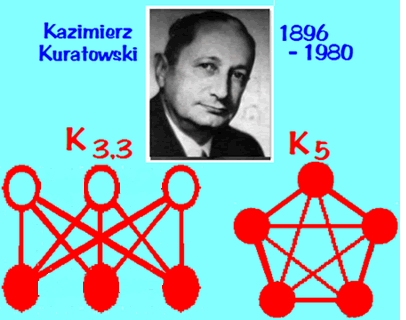
  • Any non-planar graph has a copy of one of these two graphs in it somewhere, as a subgraph:
    

This paper contains a lot of references, and on-line resources to document their work.

"Because the human brain is so good at detecting faces, we sometimes see them where they do not exist. Were you ever scared as a child by strange faces popping up from an abstract wallpaper design or formed by shadows in the semidarkness of your bedroom? Ever notice that cars seem to have faces, with the headlights as eyes and the grilles as mouths? These effects result from the face-recognition circuits of our brains, which are constantly trying to find a face in the crowd."