- Thanks to those of you who came by to support our protest on Friday! It was good to see you.
- The quiz:
- Most of you have developed a strategy for graphing these knots; good!
- The ones that we can't get from a twisted band include the figure eight, the \(5_2\) knot, and the Borromean rings. All the rest come out of our twisted bands!
- Again, most of you seem to have developed a strategy for graphing these links.
- Even numbers of twists are links; odd numbers of twists are knots.
- Two days ago I found the following on-line:
'Mind blowing': quantum computer untangles the mathematics of knots: Algorithms for studying knots and other topological objects could have a quantum advantage.
Knot invariants are typically calculated from patterns of crossings - how the threads in a knot cross over each other when the knot is flattened on a surface - but depend only on the knot's topological type. In other words, the same knot can be flattened in two different ways, with vastly different crossing patterns, but the knot invariant will still be the same. If two crossing patterns have different knot invariants, it means that they come from knots that are topologically distinct.
"Why is topology so inherent to quantum computation? I think this is a very deep question," says Aharonov. The answer, she adds, could be linked to the fact that in quantum physics, many particles can share a collective 'entangled' state, and there are quantum states that maintain their quantum information even if they change at a local level. Having properties that don't change when an object undergoes a local deformation is "very much the essence of topology", she says.
- We practiced drawing knots and links (especially the Borromean
rings, and the twist knots)
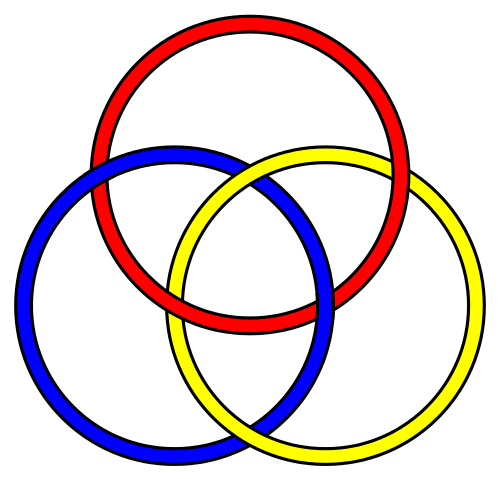

- We also built the "RCO"
-- Really Cool Object -- which brings together the Borromean rings,
golden rectangles, and Platonic solids (an icosahedron).
This is the most beautiful piece of mathematics I know:
It turns out that there are golden rectangles in the heart of an icosahedron, interlocked as Borromean rings!

We made some using 3x5 (or 4x6) cards -- which are not quite golden. Their corners are the 12 vertices of the icosahedron. The tricky part is locking them together!
- Then we had a quiz.
- A little review, and a preview of what's ahead: trying to
distinguish this collection of knots (and links, too!).
-
The figure-eight
knot has four crossings, as does Solomon's "knot" -- but
Solomon's "knot" a link, not a knot. This is the first
(interesting) instance of a knot and link with the same
(minimal) number of crossings.
But we can easily figure out which is which, because the knot is a single continuous piece of material, whereas the link is two separate pieces of material.
- We know that there are two distinct 5-crossing knots
(we can see them in Rolfsen Knot Table)
- The cinquefoil knot, which has R5 symmetry; and
- The other five-crossing knot \(5_2\), which is actually known (somewhat confusingly) as the 3-twist knot (making it sounds like a trefoil).
- How can we tell them apart? Are they really different? For that we need to study knot equivalence, and our primary tool, the Reidemeister moves.
-
The figure-eight
knot has four crossings, as does Solomon's "knot" -- but
Solomon's "knot" a link, not a knot. This is the first
(interesting) instance of a knot and link with the same
(minimal) number of crossings.
- How do we show that two knot projections ("squiggles") are the
same knot ("knot
equivalence")? That's the job of the Reidemeister
moves.
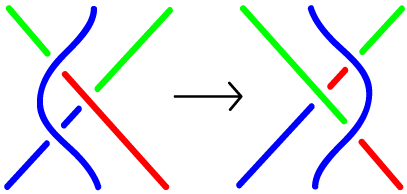
- What are the Reidemeister moves?
- Tools for showing that two projections (pictures) of knots really show the same knot.
- Names of the moves reflect the number of
strands involved. A Strand is a
piece of a knot picture that
goes from undercrossing to
undercrossing, with only
overcrossings inbetween.
It's all about overs and unders!
- Reidemeister moves preserve the knot -- they don't change the knot. We're not cutting -- we're just going to shove parts of the knot around.
-
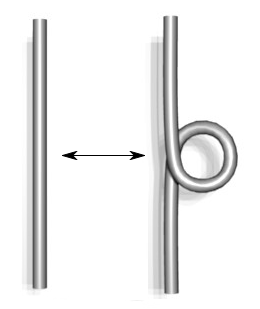
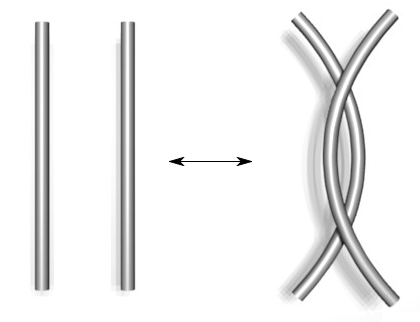
Type I Type II Type III
- Here's a
summary of the moves.
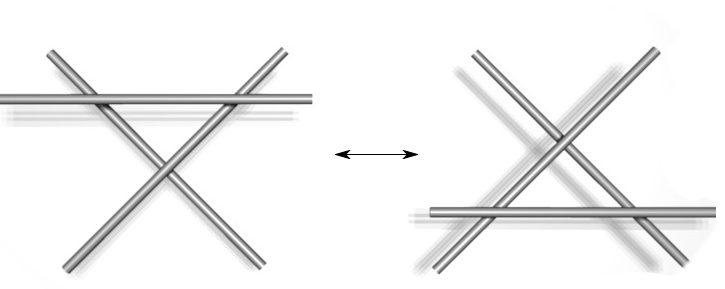
The third images on that page stems from this picture from a recent Science issue:


In order to consider the picture on the left a knot, we have to know what its ends are doing. In the figure at right, I assumed that they are just connecting to each other in the simplest way.
The succession of steps then go on to show that the knot is actually an unknot! That's good news for the hyperbusy people!
- Using the Reidemeister moves
- to turn a projection of an unknot into another
more complicated appearing unknot:

Here's another picture of an unknot, which could trick you -- but knowing the R1 move saves you:

We'll just try a few with a string, to see what we can learn.
- Now let's use these three moves to create equivalent
versions of the trefoil knot, but using each of the three
Reidemeister moves.
- A figure-eight knot is equivalent to its mirror reflection (a trefoil knot is not equivalent to its mirror!)
- Turning a more complicated appearing unknot into a simple circle unknot. (Here it is as a powerpoint presentation.)
- to turn a projection of an unknot into another
more complicated appearing unknot:
- Reidemeister moves and Tricolorability
- Tricolorability:
"A knot is tricolorable if each strand of the
knot diagram can be colored one of three
colors, subject to the following rules:
- At least two colors must be used,
- at most three colors are used, and
- at each crossing, the three incident strands are either all the same color or all different colors.
- Tricolorability is preserved by Reidemeister moves:
Reidemeister Move I is tricolorable. Reidemeister Move II is tricolorable. Reidemeister Move III is tricolorable. - Therefore, if the projection of one knot is
tricolorable and the other isn't, they're different
knots (because we can't get from one to the other via
Reidemeister moves).
- Theorem: there are at least two different knots.
- The unknot is not tricolorable ("At least two colors must be used");
- The trefoil knot is tricolorable:

- The figure-eight knot is not tricolorable (it requires four colors):


- Danger: be careful what you conclude:
- Links can be tricolorable, too -- for example, the unlink is
tricolorable! (That's just two circles, one lying on top of
the other, as in Borromean rings.)
- many knots are tricolorable -- in fact, infinitely
many! -- so being tricolorable doesn't mean that
your knot is the trefoil knot -- but it does mean that
your knot is not the unknot, for example.
So, for example: if you've got your picture of a knot down to three crossings, and it's not tricolorable, then it's the unknot.
- And among knots and links with five crossings or fewer, only the trefoil and the unlink are tricolorable.
- Links can be tricolorable, too -- for example, the unlink is
tricolorable! (That's just two circles, one lying on top of
the other, as in Borromean rings.)
- Tricolorability:
"A knot is tricolorable if each strand of the
knot diagram can be colored one of three
colors, subject to the following rules:
- What are the Reidemeister moves?
- Triangle and rectangle paper
- Shodor:
- Snowflake on-line
- Gasket on-line
- The Fractal Microscope (click on the image)
- L-Systems
in PostScript, from which I generated this image:

- Vi Hart
- L-System Fractals
- Nice website with examples of Cantor, Koch, and other fractals
- Here are some more lovely examples
- l-system generator: world's simplest math tool
- I first encountered the L-Systems fractals at britton.disted.camosun.bc.ca/fractals_arcytech/lsystems.html, but that's a dead link. However, I copied the files, and have a local copy here. However, web browsers these days don't seem to like the applet tag in javascript, so this doesn't work anymore in a standard web browser...:(