Day 35, MAT115R

If you think that you'd like to protest a change in climate in our world this Friday, something that matters to you, please join us! Talk to me, or email.

What should Danielle's political logo be? How about some Borromean rings with Integrity, Honesty, Devotion, or the like?

0. twists: The unlink
1. twists: The unknot
2. twists: The Hopf Link
3. twists: The Trefoil Knot (three leaves)
4. twists: Solomon's Knot (which is actually a link)
5. twists: Cinquefoil Knot (five leaves)

• Notice her graphs in the first part of the video: those are the two non-planar graphs, and the graph of an octahedron! (She makes a balloon octahedron.)
• At 0:57 she's creating an interesting link
• At 1:11 she begins drawing a trefoil knot oroborus (snake swallowing its own tail)
• "Borromean snakes" (1:15): "No two snakes are actually linked to each other" (1:22).
• At 1:30 she begins drawing the two distinctly different five knows: the cinquefoil, and the other five knot, which we'll call \(5_2\).
• There is another cinquefoil at 2:06: Serpentagon
• A beautifully shaded trefoil at 4:02
• Vi asks "What kind of knots are you drawing and can you classify them?" That's the question we'll discuss today.

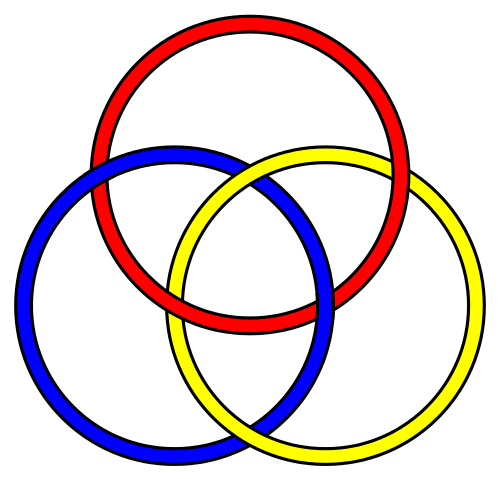
If you want to draw the Borromean rings, you'd draw three circles, as in the first figure above:	but you'd want to indicate, somehow, that one ring is below another ring (aka the "Irish Trinity"):

Let's draw those. Kamora and I were drawing these yesterday, and saw that it's not too bad:

1. Draw three overlapping circles, and don't worry about the overs and unders
2. Now start with any one circle, and decide whether the first crossing is over or under. Then alternate. You'll get four crossings correct that way. It will always works out (like Vi Hart's squiggle game).
3. That leaves two crossings, and you can start from one of your other crossings and finish off those two so that they alternate. This too will always work out.
4. Then polish it up with some nice colors, and voila!

1. twists: The Trefoil Knot
2. twists: Figure 8 Knot
3. twists: \(5_2\)

• Toroidal knots and links
• Twist knots (trefoil, figure-eight, \(5_2\))

This is the most beautiful piece of mathematics I know:

It turns out that there are golden rectangles in the heart of an icosahedron, interlocked as Borromean rings!

We'll make some using 3x5 (or 4x6) cards -- which are not quite golden. Their corners are the 12 vertices of the icosahedron. The tricky part is locking them together!

• The figure-eight knot has four crossings, as does Solomon's "knot" -- but Solomon's "knot" a link, not a knot. This is the first (interesting) instance of a knot and link with the same (minimal) number of crossings.

  But we can easily figure out which is which, because the knot is a single continuous piece of material, whereas the link is two separate pieces of material.

• We know that there are two distinct 5-crossing knots (we can see them in Rolfsen Knot Table)
  • The cinquefoil knot, which has R5 symmetry; and
  • The other five-crossing knot \(5_2\), which is actually known (somewhat confusingly) as the 3-twist knot (making it sounds like a trefoil).

• How can we tell them apart? Are they really different? For that we need to study knot equivalence, and our primary tool, the Reidemeister moves.

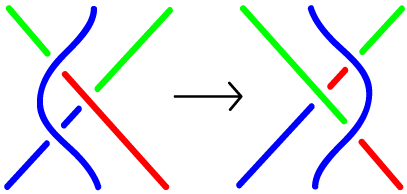
1. What are the Reidemeister moves?
   • Tools for showing that two projections (pictures) of knots really show the same knot.
   • Names of the moves reflect the number of strands involved. A Strand is a piece of a knot picture that goes from undercrossing to undercrossing, with only overcrossings inbetween.

     It's all about overs and unders!

   • Reidemeister moves preserve the knot -- they don't change the knot. We're not cutting -- we're just going to shove parts of the knot around.

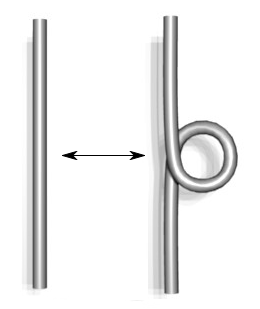
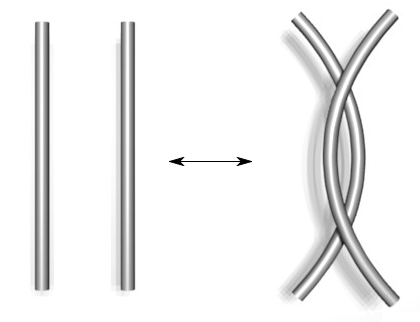
   • Type I	Type II	Type III

2. Here's a summary of the moves.

   The third images on that page stems from this picture from a recent Science issue:

   In order to consider the picture on the left a knot, we have to know what its ends are doing. In the figure at right, I assumed that they are just connecting to each other in the simplest way.

   The succession of steps then go on to show that the knot is actually an unknot! That's good news for the hyperbusy people!

3. Using the Reidemeister moves
   1. to turn a projection of an unknot into another more complicated appearing unknot:

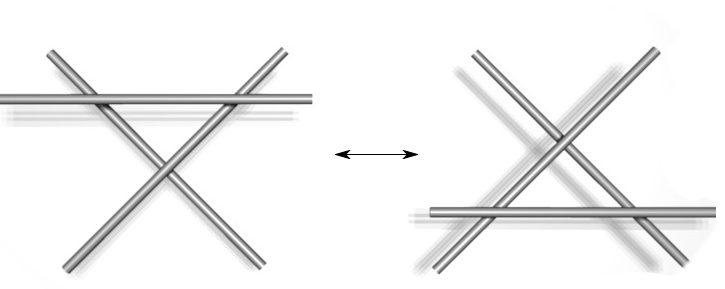
      Here's another picture of an unknot, which could trick you -- but knowing the R1 move saves you:

      

      We'll just try a few with a string, to see what we can learn.

   2. Now let's use these three moves to create equivalent versions of the trefoil knot, but using each of the three Reidemeister moves.

   3. A figure-eight knot is equivalent to its mirror reflection (a trefoil knot is not equivalent to its mirror!)

   4. Turning a more complicated appearing unknot into a simple circle unknot. (Here it is as a powerpoint presentation.)

4. Reidemeister moves and Tricolorability
   1. Tricolorability: "A knot is tricolorable if each strand of the knot diagram can be colored one of three colors, subject to the following rules:
      1. At least two colors must be used,
      2. at most three colors are used, and
      3. at each crossing, the three incident strands are either all the same color or all different colors.

   2. Tricolorability is preserved by Reidemeister moves:

      Reidemeister Move I is tricolorable.	Reidemeister Move II is tricolorable.	Reidemeister Move III is tricolorable.

   3. Therefore, if the projection of one knot is tricolorable and the other isn't, they're different knots (because we can't get from one to the other via Reidemeister moves).

   4. Theorem: there are at least two different knots.
      1. The unknot is not tricolorable ("At least two colors must be used");
      2. The trefoil knot is tricolorable:

      3. The figure-eight knot is not tricolorable (it requires four colors):
      4. Danger: be careful what you conclude:
         • Links can be tricolorable, too -- for example, the unlink is tricolorable! (That's just two circles, one lying on top of the other, as in Borromean rings.)

         • many knots are tricolorable -- in fact, infinitely many! -- so being tricolorable doesn't mean that your knot is the trefoil knot -- but it does mean that your knot is not the unknot, for example.

           So, for example: if you've got your picture of a knot down to three crossings, and it's not tricolorable, then it's the unknot.

         • And among knots and links with five crossings or fewer, only the trefoil and the unlink are tricolorable.

1. Snowflake on-line
2. Gasket on-line
3. The Fractal Microscope (click on the image)

• Vi Hart draws fractals