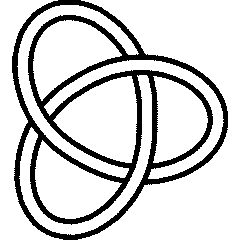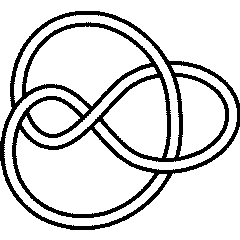Day 34, MAT115R

If you think that you'd like to protest a change in climate in our world this Friday, something that matters to you, please join us! Talk to me, or email.

We produced six objects, three links and three knots:

0. twists: The unlink
1. twists: The unknot
2. twists: The Hopf Link
3. twists: The Trefoil Knot (three leaves)
4. twists: Solomon's Knot (which is actually a link)
5. twists: Cinquefoil Knot (five leaves)

A couple of important things:

• rotational symmetry!
• regular polygons!
• alternating overs and unders

• Notice her graphs in the first part of the video: those are the two non-planar graphs, and the graph of an octahedron! (She makes a balloon octahedron.)
• At 0:57 she's creating an interesting link
• At 1:11 she begins drawing a trefoil knot oroborus (snake swallowing its own tail)
• "Borromean snakes" (1:15): "No two snakes are actually linked to each other" (1:22).
• At 1:30 she begins drawing the two distinctly different five knows: the cinquefoil, and the other five knot, which we'll call \(5_2\).
• There is another cinquefoil at 2:06: Serpentagon
• A beautifully shaded trefoil at 4:02
• "What kind of knots are you drawing and can you classify them?"

• Links are like the links you find in chains: constructed by "linking" loops (or rings) together.

• Perhaps the most famous links in the world are the Olympic rings:

  Wikipedia	Here are the originals

  Are they the same?

• Borromean Rings: "Is it possible to create a link of three loops (or rings) in such a manner that they are indeed linked, yet if we remove any one of the rings the other two become unlinked?"

• Yes, indeed!

  Standard diagram of the Borromean rings

  A realization of the Borromean rings as ellipses

  Coat of arms (of the municipality of Hallsberg, Sweden) showing padlocks in Borromean rings configuration

  
  (Thanks Wikipedia!)

• More on the Borromean rings:
  • I always think of them in the context of this quote:

    "We must all hang together, or assuredly we shall all hang separately." Benjamin Franklin, at the signing of the Declaration of Independence.

  • Led Zeppelin, in the album sleeve of their album Led Zeppelin IV used it:

    "Drummer John Bonham's symbol, the three interlocking rings, was picked by the drummer from [Rudolf Koch's Book of Signs]. It represents the triad of mother, father and child, but also happens to be the logo for Ballantine beer." (from the Wikipedia article on Led Zeppelin IV).

    

    (thanks Matt!).

    Ironically I just discovered John Paul Jones's symbol in another brewing company (while enjoying one of their products); Arcadia Brewing company of Kalamazoo, Michigan, has this as their logo:

    

    Maybe every Led Zepellin symbol is on a beer somewhere?

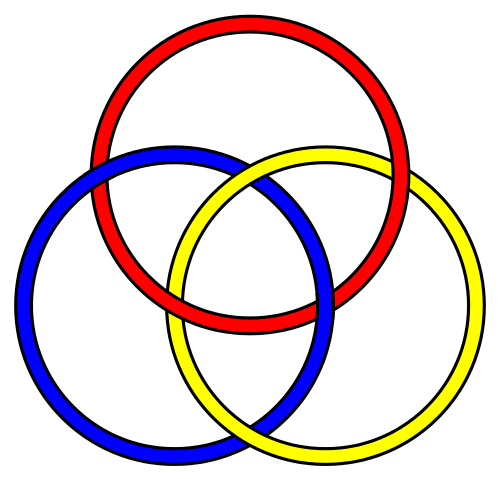
  • If you want to draw the Borromean rings, you'd draw three circles, as in the first figure above:	but you'd want to indicate, somehow, that one ring is below another ring (aka the "Irish Trinity"):

    Let's try making the borromean rings with rubber bands.

    One more:

    

    Scene from Stora Hammar stone

    with a closeup of the rings:

• Now it's back to knots. Let's see how to create our last two knots, which are called "twist knots" (sadly enough, because that risks confusing them with our twisted band knots!).
  • Knot Theory
    • We begin with the "unknot", of course: a circle. This is the simplest knot, but not very interesting.

    • Trefoil Knot -- the simplest interesting knot. It has three crossings, and there's no way to make it any simpler! We will also call it the 3-knot:
      

    • Can we make a simpler knot -- one with either 1 or 2 crossings? Why not?

    • There are two different ways to think about making the trefoil knot: as a
      1. twist knot, and as a
      2. torus knot (the way we were making them using twisted bands -- which we can think of as icing on a donut -- a torus!).
      Let's draw it in these two different ways.

    • The figure-eight knot:
      

    • And the last of our "knots to know": The five-crossing knot \(5_2\) (and here's a gallery of all knots up to seven crossings)

      Here's a picture of it (and it's pretty, but I like its picture better in the gallery mentioned above):

      

  • Now let's migrate our discussion of knots over to "Knot Mosaics":
    

    (an example of Solomon's Knot -- which you might notice is actually a link!)

    • Celtic Knot Mosaic Examples: (not quite the same idea, but pretty! And again, you'll see that there are links contained therein -- including Borromean rings)
      • Triangular paper (in case you want to try making some of those).

    • Knot Mosaics
      • help us to draw Borromean Rings, for example: use your Mosaic Graph Paper to create your own version of the Borromean Rings.
      • Rectangular Mosaic Tiles and symmetry
      • We can use them to make any knots: try your hand at
        • the trefoil knot:
          

        • The figure-eight knot:
          

  • Something fun to do with a few friends: can we make a human knot in the shape of a trefoil knot? If so, then we won't be able to undo it -- you and your friends will be knotted together forever! I hope that's a good thing....

1. Snowflake on-line
2. Gasket on-line
3. The Fractal Microscope (click on the image)

• Vi Hart draws fractals