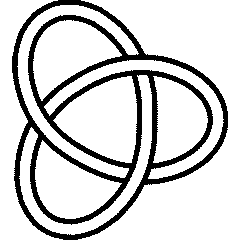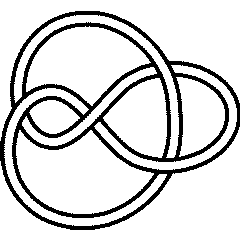Day 33, MAT115R

• Reminder: I'm helping to organize and staff an event this Friday, April 11: Support Climate Action on Campus

  If you think that you'd like to protest a change in climate in our world this Friday, something that matters to you, please join us! Talk to me, or email.

  We could especially use help making signs and decorating our mannequin(s) (this Wednesday at 9:00 am), as well as creating some fun activities!

• Quiz this week will be over our first twisted bands, including the Mobius strip.

• Our exam
  • The exam
  • The key
  • Median: 72.5
  • Some comments:
    • Your final exam grade will replace your lowest midterm grade.
    • Your final exam will feature problems that look a lot like those of your two midterms. Learn from your mistakes!

• Let's talk about projects. Originally I had intended to incorporate Mathemalchemy into our projects, but we haven't made much use of Mathemalchemy. So I'm going to extend our project definition. Let's visit that for a moment.

• The Mobius Band was the focal point, "the band that never ends".

  We learned that

  • A Mobius band is made by giving a strip of paper a half twist.
  • It only has one side, and one edge. Today we'll draw some (hopefully some of you are better draw-ers than I!).
  • The Mobius band has left- and right-handed versions, which cannot be transformed into each other.
  • Cut one down the middle, and you get a longer band (twice-twisted); but cut that down the middle, and you get two bands, linked together (in a Hopf Link).

  That's because one had an odd number of twists and the other had an even number of twists.

• We cut a thrice-twisted band, and got our first interesting knot: the trefoil knot.
• We cut a frice-twisted band (that's four twists!), and got our first interesting link: the Solomon's Knot (which is a link!)
• Then we squashed Mobius bands, to make the official recycling symbol and the other (fake!) version that has rotational symmetry of order three:
  

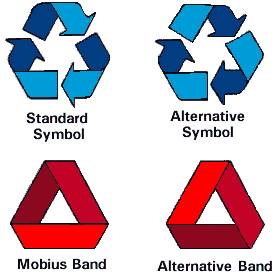
  Which reminds me of a logo (remember your logos, which will be presented in just a few weeks?)

  

Today is just a "gentle introduction to links and knots". Next time we'll start in on how to distinguish them, which involves a little more mathematics.

• Let's begin by watching a video from Vi Hart, about snakes and graphs, and playing her "squiggle graph game".

  It turns out that a lot of what we do is going to be about "overs and unders" -- which strand is on top of another strand. And that's the focus of her game.

  • This was assigned because it relates to both graphs and to knots and links. Vi is doing double duty for us here! (I hope that you also watched her video about the Mobius Music Box).
  • Notice her graphs in the first part of the video: those are the two non-planar graphs, and the graph of an octahedron!
  • By making a closed-curve squiggle graph, you're creating a knot. (A knot is a single piece of string, in which the two cut ends are ultimately tied back together to create a single continuous piece of string -- which may be "knotted"!)
  • "Borromean snakes": "No two snakes are actually linked to each other" (1:22).
  • Just before the Borromean snakes there is a trefoil snake (1:14).
  • "What kind of knots are you drawing and can you classify them?"

• Time to create some knots and links in a methodical fashion.

  How does a twisted band relate to links and knots? Let's try to draw some edges:

  • Draw what I call "the wedding band" -- an untwisted band.
  • Draw the edge of a Mobius band (once-twisted).
  • Draw the edge of a twice-twisted band.
  • Draw the edge of a thrice-twisted band.
  • Draw the edge of a fourice-twisted band.
  • Draw the edge of a fiveice-twisted band.
  This class of objects will lead us to the notions of links and knots....

• Links:
  • Links are like the links you find in chains: constructed by "linking" loops (or rings) together.

  • Perhaps the most famous links in the world are the Olympic rings:

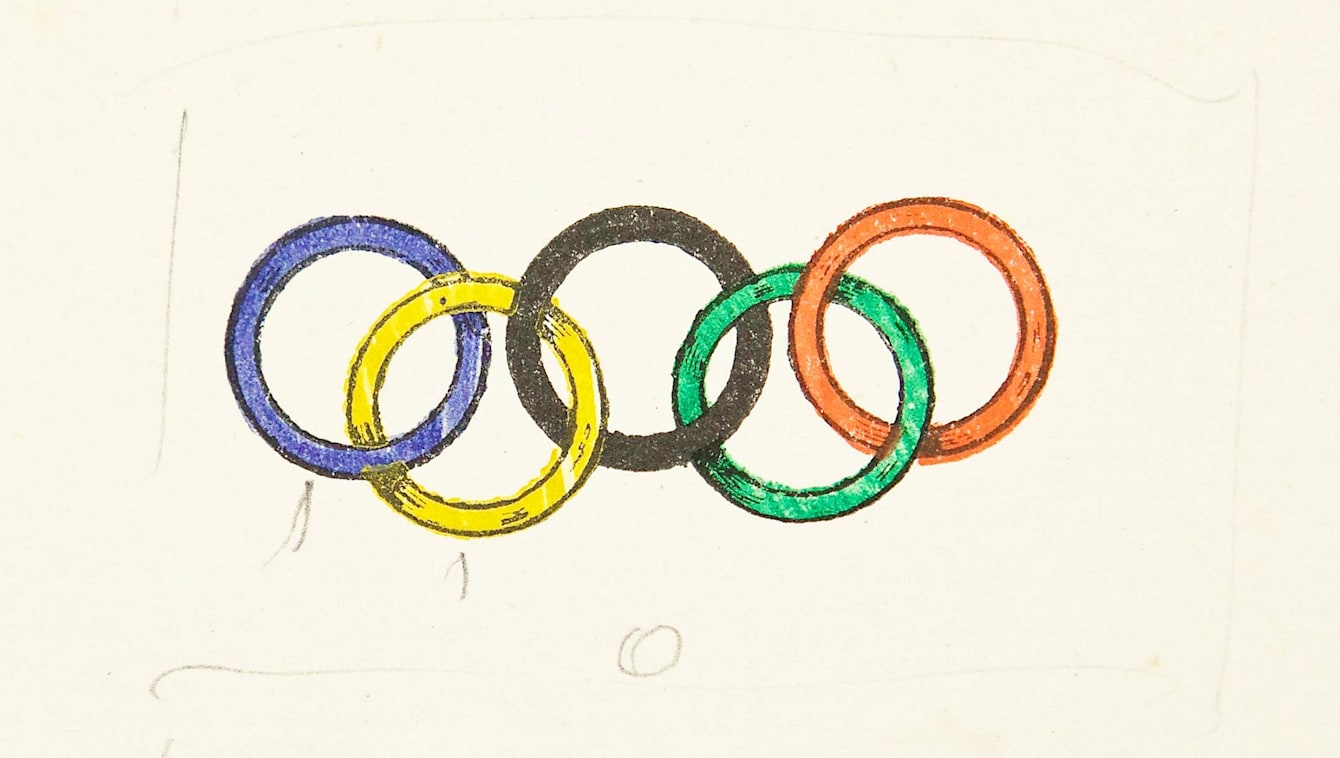
    Wikipedia	Here are the originals

    Are they the same?

  • Borromean Rings: "Is it possible to create a link of three loops (or rings) in such a manner that they are indeed linked, yet if we remove any one of the rings the other two become unlinked?"

  • Yes, indeed! Let's try it with rubber bands first.

    Standard diagram of the Borromean rings

    A realization of the Borromean rings as ellipses

    Coat of arms (of the municipality of Hallsberg, Sweden) showing padlocks in Borromean rings configuration

    
    (Thanks Wikipedia!)

  • More on the Borromean rings:
    • I always think of them in the context of this quote:

      "We must all hang together, or assuredly we shall all hang separately." Benjamin Franklin, at the signing of the Declaration of Independence.

    • Led Zeppelin, in the album sleeve of their album Led Zeppelin IV used it:

      "Drummer John Bonham's symbol, the three interlocking rings, was picked by the drummer from [Rudolf Koch's Book of Signs]. It represents the triad of mother, father and child, but also happens to be the logo for Ballantine beer." (from the Wikipedia article on Led Zeppelin IV).

      

      (thanks Matt!).

      Ironically I just discovered John Paul Jones's symbol in another brewing company (while enjoying one of their products); Arcadia Brewing company of Kalamazoo, Michigan, has this as their logo:

      

      Maybe every Led Zepellin symbol is on a beer somewhere?

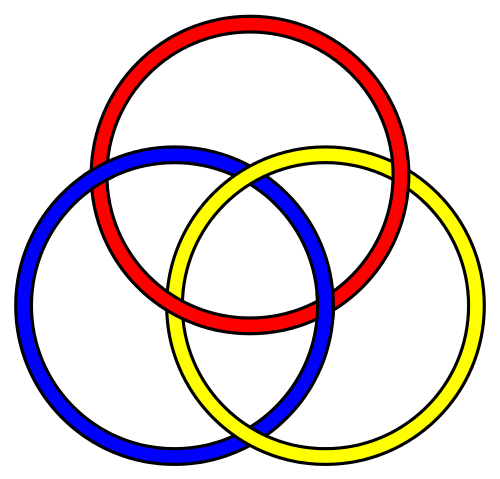
    • If you want to draw the Borromean rings, you'd draw three circles, as in the first figure above:	but you'd want to indicate, somehow, that one ring is below another ring (aka the "Irish Trinity"):

      One more:

      

      Scene from Stora Hammar stone

      with a closeup of the rings:

  • Now it's back to knots. Let's see how to create our last two knots, which are called "twist knots".
    • Knot Theory
      • We begin with the "unknot", of course: a circle. This is the simplest knot, but not very interesting.

      • Trefoil Knot -- the simplest interesting knot. It has three crossings, and there's no way to make it any simpler! We will also call it the 3-knot:
        

      • Can we make a simpler knot -- one with either 1 or 2 crossings? Why not?

      • There are two different ways to think about making the trefoil knot: as a
        1. twist knot, and as a
        2. torus knot.
        Let's draw it in these two different ways.

      • The figure-eight knot:
        

    • Now let's migrate our discussion of knots over to "Knot Mosaics":
      

      (an example of Solomon's Knot -- which you might notice is actually a link!)

      • Celtic Knot Mosaic Examples: (not quite the same idea, but pretty! And again, you'll see that there are links contained therein -- including Borromean rings)
        • Triangular paper (in case you want to try making some of those).

      • Knot Mosaics
        • help us to draw Borromean Rings, for example: use your Mosaic Graph Paper to create your own version of the Borromean Rings.
        • Rectangular Mosaic Tiles and symmetry
        • We can use them to make any knots: try your hand at
          • the trefoil knot:
            

          • The figure-eight knot:
            

    • Something fun to do with a few friends: can we make a human knot in the shape of a trefoil knot? If so, then we won't be able to undo it -- you and your friends will be knotted together forever! I hope that's a good thing....

• Triangle and rectangle paper
• Shodor:
  1. Snowflake on-line
  2. Gasket on-line
  3. The Fractal Microscope (click on the image)

• L-Systems in PostScript, from which I generated this image:
  

• Vi Hart
  • Vi Hart draws fractals
• L-System Fractals
• Nice website with examples of Cantor, Koch, and other fractals
• Here are some more lovely examples
• l-system generator: world's simplest math tool
• I first encountered the L-Systems fractals at britton.disted.camosun.bc.ca/fractals_arcytech/lsystems.html, but that's a dead link. However, I copied the files, and have a local copy here. However, web browsers these days don't seem to like the applet tag in javascript, so this doesn't work anymore in a standard web browser...:(