- Section 2.8 (Using Derivatives to Evaluate Limits) will be the
subject of our quiz Friday. Any questions on that?
- Your exam corrections are due Friday, along with your original exam.
- We went over the exam, and the key.
- We went over some examples of L'Hôpital's rule, in particular in some different situations (e.g. quotients where numberator and denominator to go infinity; or non-quotients, which can be converted to quotients.
- Then we got started on section 3.1 (Using derivatives to identify extreme values).
- We looked at an example problem -- building a rectangular pen of maximal area, using a given quantity of fencing -- and saw that we could solve the problem in two different ways: with algebra, and our understanding of functions (parabolas, in this case); and we confirmed that calculus gave us the same answer. Good!
- We continue to talk about the extrema -- that is, maxima and minima --
places where a function takes on extreme values. One of the
most important roles of the derivative is to identify those
places where a function hits its maximum or minimum.
- Let's continue to reflect on the example from last time: my pen
for Ace.
We saw that if we make his pen rectangular (and "free-standing") then we should make it in the shape of a square. That should be somewhat satisfying! Some solutions feel intuitively correct.
I have a big old barn: what if we can use an existing wall, e.g. the side of a long barn? What would the dimensions be? What do you think?
We still have a constraint: 200 meters of fencing.
Now the two dimensions in our picture (remember to draw a picture, and provide good variable names?) are related by \[ 2w+l=200 \]
so \[ l=200 - 2w=2(100 - w) \]
Therefore \[ A(w)=2w*(100-w) \]
No need to differentiate: this is just twice the previous equation, so it has the same critical point: \[ A'(w)=100 - 2w = 0 \textrm{ when } w=50 \] But now the length is 100m. You might think of this as two of the previous square pens glued together!
Did you expect that shape? Maybe you thought that it would be square again... Here's where calculus helps! Whatever we might think, calculus may well be able to provide the right answer.
- The point is that these sorts of problems, when they can be
formulated as functions, present opportunities for
"optimization"; and the derivative is the tool that will help
us locate the extrema, or "optimal" values of something.
Generally we seek the global maximum or the global minimum -- which we have found in the cases above. Because those functions were quadratics, we know that they have only one point on their graphs where the derivative is zero -- and no points where their derivatives don't exist (although there were boundaries beyond which we couldn't go -- no lengths or widths were to be negative, for example).
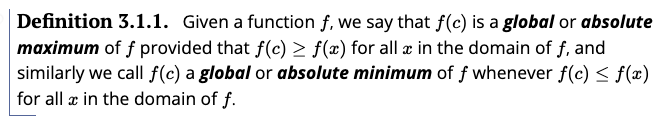
Notice that there can be ties! Thus a constant function \(x=a\) has global extrema everywhere.
One other important consideration is the domain. In those problems, the dimensions had to be positive. So we could have constrained the solutions to be where both $w>0$ and $l>0$.
This sets up the possibility for the maximum or minimum to be at the border (as is true in this case -- the global minimum is 0 -- if we run the fencing the whole length, so that it's all length, with $w=0$. This results in a fence that Ace won't like at all! (Remember that we don't want to kill Ace by squishing him into a pen of width zero!)
Furthermore, however, we might have local "extrema" (maxes or mins), that, while larger than their neighbors, give Ace only a local advantage -- but a better solution could be found elsewhere in the domain:
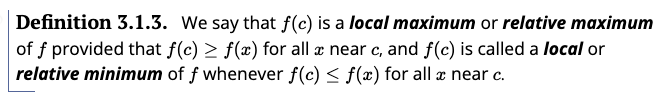
- Now let's consider a more pathological function: that of the
preview for this section:
and this set of images showing (some of) the kinds of things that can go wrong (at least in the case of a continuous function -- if you introduce discontinuities, things can get uglier):
Figure 3.1.5. From left to right,
- a function with a relative maximum where its derivative is zero;
- a function with a relative maximum where its derivative is undefined;
- a function with neither a maximum nor a minimum at a point where its derivative is zero (so there is no guarantee that there will be an extremum just because the derivative is zero);
- a function with a relative minimum where its derivative is zero;
- and a function with a relative minimum where its derivative is undefined.
These \(x\)-values, these places where the derivative is zero or doesn't exist are called critical points, or critical numbers.
- There are two important tests in this section which we can deduce
from the graphic above:
- The first
derivative test: Let $c$ be a critical number of a
continuous (that's important!) function $f$.
- If $f^\prime$ changes sign from positive to negative at $c$, then $f$ has a local maximum at $c$.
- If $f^\prime$ changes sign from negative to positive at $c$, then $f$ has a local minimum at $c$.
- If $f^\prime$ does not change sign at $c$, then $f$ has neither a max nor a min at $c$.
- Second derivative test: Suppose $f^{\prime\prime}$ is
continuous near $c$.
- If $f^{\prime}(c)=0$ and $f^{\prime\prime}(c)>0$, then $f$ has a local minimum at $c$;
- If $f^{\prime}(c)=0$ and $f^{\prime\prime}(c)<0$, then $f$ has a local maximum at $c$.
- The first
derivative test: Let $c$ be a critical number of a
continuous (that's important!) function $f$.
- Let's try out Activity 3.1.2 from this section, and then we'll turn
to the worksheet for 3.1.
Here's the graph of the derivative discussed in that activity:
Try plotting \[ \frac{x^3}{3}+2 x^2+x+6 \ln(|x-2|)-\frac{38}{3} \] (restrict the range to (-10,50)) and see what you think.)
- Chain Rule summary
- Mathematica for worksheet for 3.1.
- Implicit differentiation summary
- A Keeling Analysis in Mathematica
- Case Study: Early Blooming of the cherry trees in the nation's capital

