- You have a quiz on Thursday over 1.6/1.8.
- Your 1.6 homework is due to be handed in today.
- Please put your rectangles away.
- What is the difference between continuous and discontinuous
things?
- A new administration in government?
- A sidewalk?
- Coffee poured into a cup?
The key is connectedness. Continuous things don't have to be smooth, although we often think of them that way. But we certainly don't want to encounter cliffs....
- Definition: continuity at the point $x=a$:
\[
\lim_{x\rightarrow{a}}f(x)=f(a)
\]
Note: three things have to happen:
- The limit of $f$ exists at $a$,
- The function value $f(a)$ exists at $a$, and
- The two values are equal.
Otherwise $f$ is discontinuous at $a$.
There are various kinds of discontinuity (which we've already seen):
- Removable discontinuities (e.g. holes)
- Jump discontinuities
- Infinite discontinuities
- "Crazy discontinuities" like the function of #59, p. 71: $x^2$ for rational values of $x$, and 0 for irrational ones.
- Maybe a better definition:
A function is continuous on an interval if its graph can be traced there without lifting the pencil from the paper. (Try one! Make one smooth, and one really "jaggy".) Only one thing: Make sure that you're drawing a function! - Many of the functions we've considered so far satisfy this, although not all do: consider the "holy function"
\[
f(x)=\frac{\cos(x)-1}{x^2}
\]
Open Filled (and continuous):
$f(0)\equiv -0.5$This function has a limit at zero (-.5), but is not defined there. If $f$ is not defined at $x=0$, then it cannot be continuous there. We can fix this, by the way.... Just define $f(0)$ to be the limit (the closed dot in the graph above).
- Since continuity is wrapped up with limits, we have the same kinds
of results that we did in relation to limits:
- We define one-sided continuity
- we have sum laws, product, and quotient laws. We've already used these to demonstrate that polynomials are continuous on all real numbers: \[ \lim_{x\to{a}}P(x)=P(a) \]
- Classes of functions that are continuous on their domains:
- Polynomials
- Rational functions: (ratios of polynomials)
- Trigonometric functions: sine, cosine, tangent
- Root functions: $f(x)=x^{1/n}$
- Exponential functions: $f(x)=b^x$
- For all these functions one can evaluate limits using the
so-called "substitution method": simply plug in $a$ for
$x$.
- An important theorem (p. 88), RE composite functions (remember
that I told you how important compositions are? Here's another place
they show up....):
- Roughly: the composition of continuous functions is
continuous.
- Let $F(x)=f(g(x))$ be a composite function.
If $g$ is continuous at $x=a$ and $f$ is continuous at $g(a)$ then
$F(x)$ is continuous at $x=a$: \[ \lim\limits_{x\to a}F(x)=\lim\limits_{x\to a}f(g(x))=f(\lim\limits_{x\to a}g(x))=f(g(a))=F(a) \]
- Roughly: the composition of continuous functions is
continuous.
- Examples:
- pp. 90-93, #3, 10, 12, 19, 23, 36, 46 (with Mathematica)
- That crazy function which was $x^2$ for rational values of $x$, and 0 for irrational ones, has an interesting property: it is continuous at only a single point! It satisfies the definition only at $x=0$: it's discontinuous everywhere else! That's pretty weird.
- The Intermediate Value Theorem (IVT) is an important result of continuity:
- Theorem: Suppose that f is continuous on the
closed interval [a,b] and let N be any number
between f(a) and f(b), where
$f(a)\ne{f(b)}$. Then there exists a number $c$ in $(a,b)$ such
that $f(c)=N$.
This theorem is often used to show that a function has a root (that is, a value $x=c$ where $f(c)=0$): we show that it's negative at point $a$, positive at point $b$, and that it's continuous between -- hence there must be a point $c$ at which $f(c)=0$, by the IVT.
- Example: pp. 93, #69
- Theorem: Suppose that f is continuous on the
closed interval [a,b] and let N be any number
between f(a) and f(b), where
$f(a)\ne{f(b)}$. Then there exists a number $c$ in $(a,b)$ such
that $f(c)=N$.
- We lead into the derivatives by discussing secants, tangents, limits.
These are tangent lines (places where a line osculates a curve):
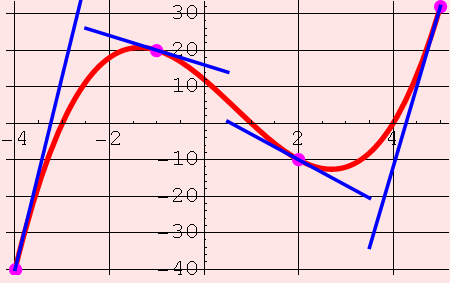
And the slopes of these tangent lines are instantaneous "rates of change" of the function f at the point of tangency. What does that mean?
The thing that tells you how fast a function is changing is its slope, isn't it?
We often represent change in mathematics by a "delta", $\Delta$. So the slope is a change in $y=f(x)$, which we might call $\Delta y$, divided by a change in $x$, or $\Delta x$: \[ slope=\frac{\Delta y}{\Delta x}=\frac{rise}{run} \] So this quantity tells how how fast $y$ is changing given a change in $x$.
- If a function is constant, then it's not changing at all ($\Delta y = 0$).
- If the slope is steep (either up or down), then the function's values are changing dramatically and quickly ($\Delta y$ large).
The rate of change is dictated by the slope. So it should come as no surprise that the derivative of a function, which is the rate of change of a function at a point, is the same as the slope of the tangent line at a point:
We can approximate tangent lines with secant lines:
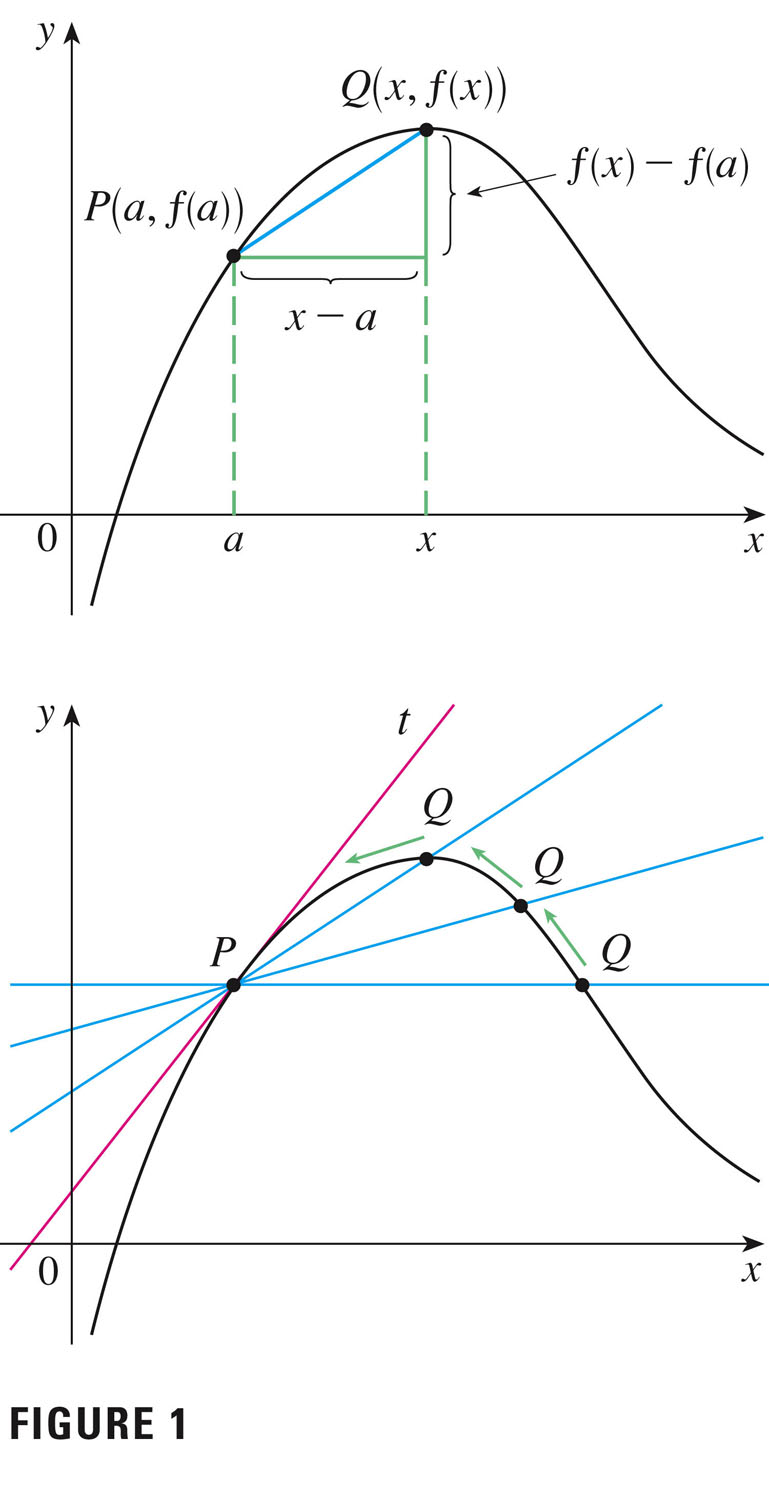
The slope m of the tangent line at P(a,f(a)) is approximated by the slope of the blue line segment (the slope of a secant line), $\frac{f(x)-f(a)}{x-a}=\frac{\Delta y}{\Delta x}$ This is an average rate of change in f over a finite interval.
In the limit, this average rate of change becomes an instantaneous rate of change:
$m=\lim\limits_{x\to{a}}\frac{f(x)-f(a)}{x-a}$ 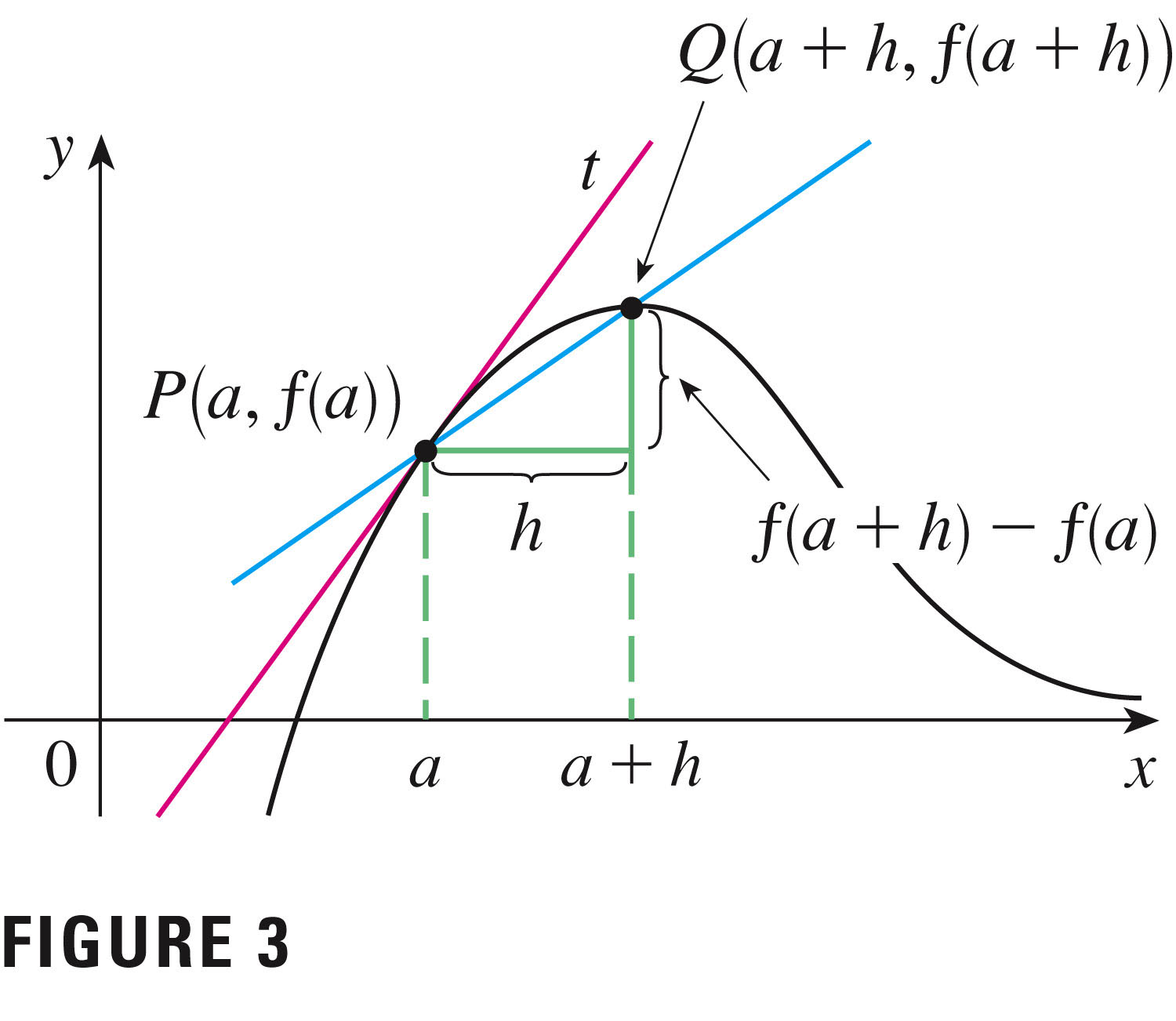
Here's an alternative notation for the slope: The slope m of the tangent line at P(a,f(a)) is approximated by the slope of the blue line segment,
$\frac{f(a+h)-f(a)}{h}$ In the limit, this is
$m=\lim\limits_{h\to 0}\frac{f(a+h)-f(a)}{h}$ which I call the most important definition in calculus. This is the formula for the derivative at a point: I've already shared with you this definition of the derivative, at any value of $x$.
- Definition of the derivative at a point: well, it's just a slope, isn't it:
$f^\prime(a) = \lim\limits_{h \to 0} \frac{f(a+h)-f(a)}{h} = \lim\limits_{x \to a} \frac{f(x)-f(a)}{x-a}$
The most important definition in calculus! (I just can't say it enough!)
Now let's look at some problems, and see how this concept is connected to real-world problems.
First, however, a word on the examples in this section: you see that, for the most part, we're using the definition(s) of a derivative to compute a slope of a tangent line. The tricky part is often writing the composition correctly -- i.e. just properly using the definition. Then you have to use a little algebra to remove the indeterminacy.
- #3, pp. 110, etc.
- #11, pp. 111
- #13, pp. 111
- #29, pp. 112
- #45, pp. 112
- #51, pp. 113