- Your quiz is returned.
- Your 2.1 homework is returned (graded #14 and 32)
- 2.2 is due today.
- Your first exam is this Thursday, 2/8, and will cover up
through section 2.2: that's five sections -- 1.5, 1.6, 1.8, 2.1, and 2.2.
You should review those five sections, review your notes, and look over the examples that we've done in class, your quizzes, your homework, etc. Things on the exam should look familiar.
I've told you flat out some of the things that you're going to see on this, if you've been paying attention.
I don't do study guides, because students have weaponized them: if I ask something that's not explicitly on the study guide, students will complain that I've done something unfair. So why would I tie my hands?
- Please put your rectangles away.
Let's do a few more examples.
- So the algebra was really ugly to use the definition to
find the derivative of that radical function in #25. That was
nasty, wasn't it? Wouldn't it be nice if we could avoid all of that?
Well we can, using some rules that are derived from the limit
definition of the derivative.
- So now we'll use the definition of the derivative to prove
several of the formulas in this section. We've already proven
the first two rules (constant functions $f(x)=c$ and the
linear function $f(x)=x$).
- Rules that help us avoid having to use the definition each time
(with Proofs):
- The constant multiple rule (makes sense)
$(cf(x))'=cf'(x)$ -
- The sum rule
- works as we'd hope: "The derivative of a sum is the sum of the derivatives."
$(f(x) + g(x))'=f'(x)+g'(x)$ - The product rule (doesn't work the way we'd hope):
$(f(x) \cdot g(x))'=f'(x)g(x)+f(x)g'(x)$ To prove it we use one of my favorite tricks: the addition of a special form of 0.
- The power rule:
$(x^n)'=n x^{n-1}$ where $n$ is a positive integer.
We can prove this via dominoes -- i.e., mathematical induction -- or via the binomial theorem)
- NOTE: at this point we have all the rules necessary
to differentiate all polynomials, without needing to
resort to the definition!
The derivative of the monomial $x^n$ is $nx^{n-1}$, and
The derivative of the monomial $c x^n$ is $nc x^{n-1}$ (by constant multiple).
A polynomial is just a sum of these. So we apply the sum rule, and the power rule, and the constant multiple rule to the flight of the eraser, to get
$s'(t)=(at^2+bt+c)'=2at+b$
and
$s''(t)=(2at+b)'=2a$
The general rule for a polynomial $P(x)$, where is \[ P(x)=\sum_{k=0}^n c_{k}x^k \] is \[ P'(x)=\left(\sum_{k=0}^n c_{k}x^k\right)'=\sum_{k=0}^n (c_{k}x^k)'=\sum_{k=1}^n c_{k}kx^{k-1} \] Notice that the 0-term disappears, because it's a constant, and a constant's derivative is 0 (so that term "disappears").
- The constant multiple rule (makes sense)
- Other rules:
- The quotient rule:
low d high minus high d low,
over the denominator squared they go.$\left(\frac{f(x)}{g(x)}\right)'=\frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}$
- The power rule actually works even for non-integers:
$(x^n)'=n x^{n-1}$ where $n$ is any non-zero real number (although we won't prove that).
- The quotient rule:
- Rules that help us avoid having to use the definition each time
(with Proofs):
- Examples:
- #13, p. 136
- #22, p. 136 (expand first)
- #48, p. 137
- #58, p. 137
- The derivatives of trig functions rely on some basic
understanding of the circle:
- Radian measure: there is a linear relationship between radians and degrees:
\[
Radians=\frac{2\pi}{360}Degrees
\]
In calculus, we almost always use radians. You should
try to start thinking in terms of radians, too.
- Length of a sector, related to angle $\theta$ subtending
and radius $r$:
Arc Length: $L = \theta r$
Again, this is an example of a linear relationship, but it's called "bi-linear", because it's linear in two different ways: $L$ is proportional to each of $\theta$ and $r$. So
- if you double the radius, you double the arc length;
- if you double the angle, you double the arc length.
Now you might wonder if there should be, or could be, an extra constant in there, but you can see that the formula works out for the circumference formula for a circle: \[ \theta=2\pi, \textrm{ so } L=2 \pi r \]
Yep! That's the formula for the circumference of a circle.
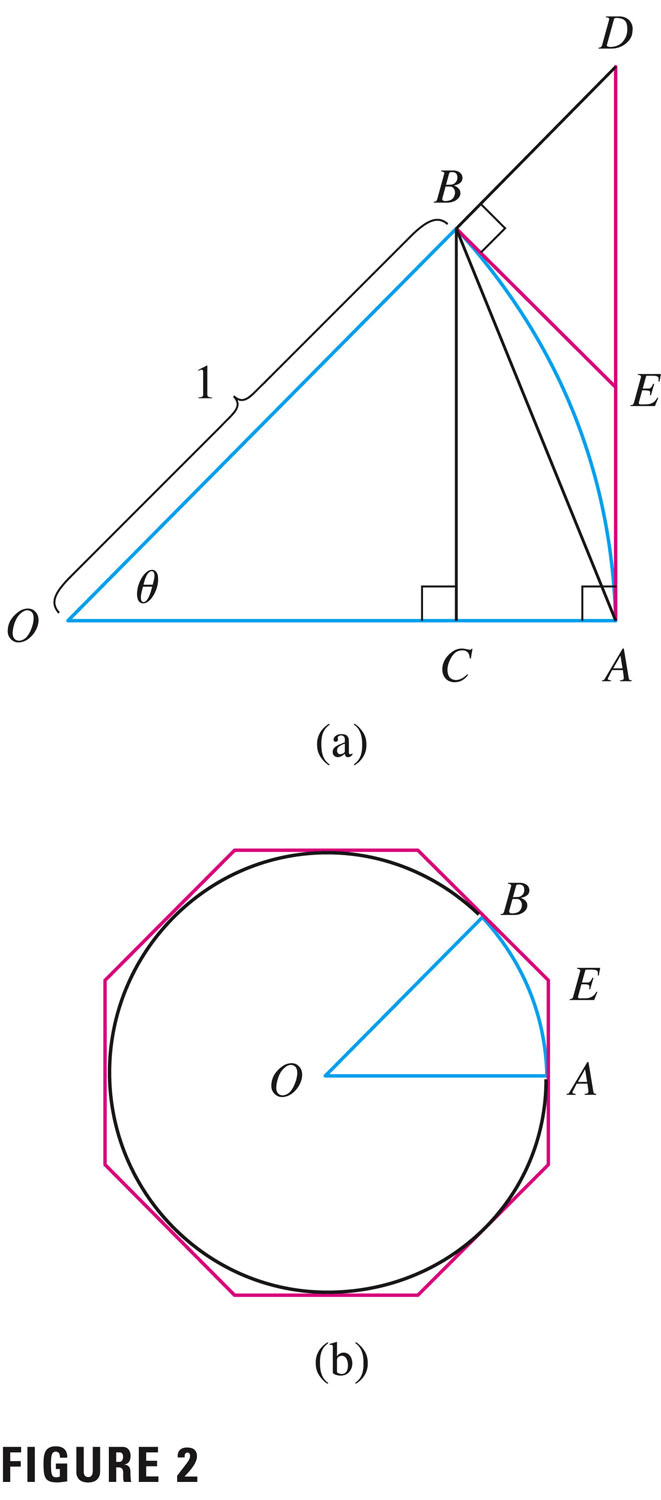
We can use this diagram (and the arc length formula) to prove a really important limit: \[ \lim\limits_{\theta \to 0}{\frac{\sin(\theta)}{\theta}}=1 \]
(See page 142, which I'll walk you through now. The proof uses some elementary trigonometry, plus the squeeze theorem, which is one of the really cool things about this proof!)
- Definitions of the trig functions, as functions of $x$, in radians (which is how we think about them in calculus):
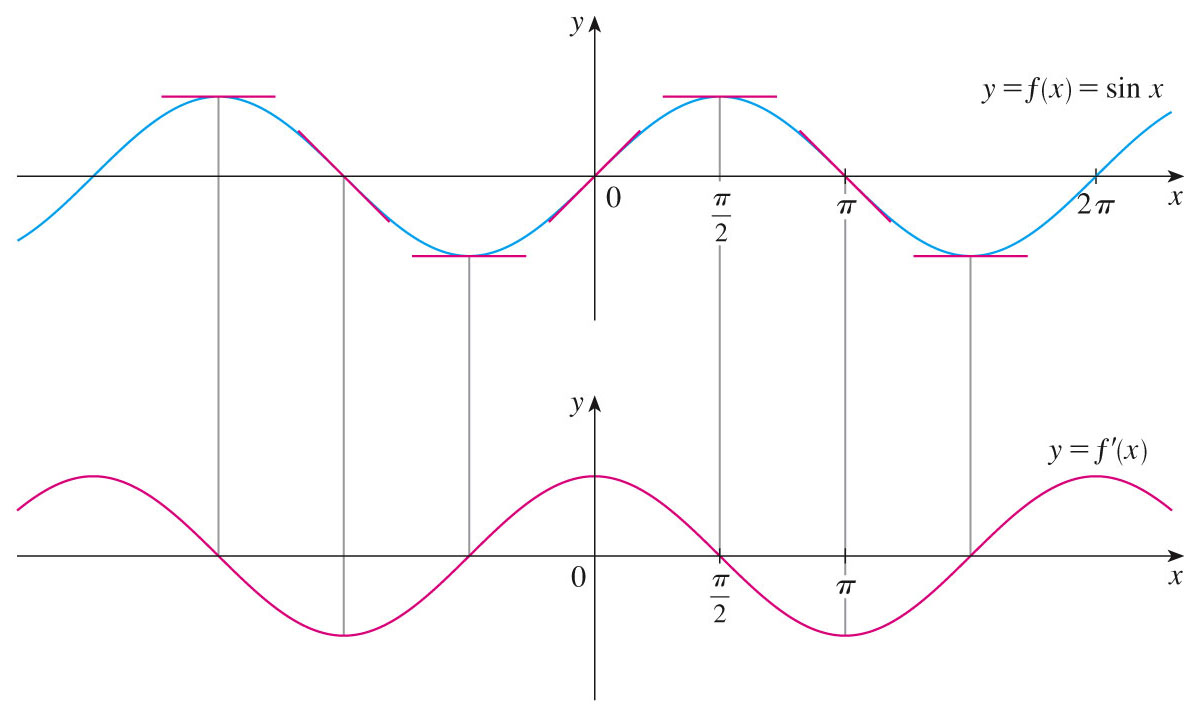
We will derive the derivative of the sine function from the limit definition of the derivative (although we can see the derivative graphically above).
There are exactly three important trig identities one needs to know (all the others can be derived from these three):
- The Pythagorean theorem:
$\sin^2(x)+\cos^2(x)=1$ - The sine of a sum:
$\sin(a+b)=\sin(a)\cos(b)+\sin(b)\cos(a)$ - The cosine of a sum:
$\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)$
So let's see how to derive the derivative of the sine from the MIDIC -- the Most Important Definition In Calculus -- the limit definition of the derivative -- using the second of these identities, plus one more important limit: \[ \lim\limits_{\theta \to 0}{\frac{\cos(\theta)-1}{\theta}}=0 \]
Then the derivative of the cosine can be derived by simply shifting the sine function, and using the second trig identity above.
- Radian measure: there is a linear relationship between radians and degrees:
\[
Radians=\frac{2\pi}{360}Degrees
\]
In calculus, we almost always use radians. You should
try to start thinking in terms of radians, too.
- Examples:
- Derivative of tangent (use the quotient rule, of course!)
- Fourth derivatives of sine, cosine
- #7, p. 146
- #26
- #35
- #49