- Your homework is returned (2.5). Graded 17, 58, and 78.
- Your quiz is returned.
- Please put your rectangles away.
I've talked a bit about how the approximation $\sin(x) \approx x$ when $x$ is small is important in physics. That is mentioned in this section, which is one reason why I wanted to have a look at 2.9:
More generally, we frequently use the linear function representing the tangent line at a point to make certain approximations.
That linear function is called the linearization of $f$ at $a$:
- For example, suppose you need to compute $\sqrt{15.96}$. Now the
easy way is to use your calculator, but the cowboy way would be to use
the linearization! Let's have a go at that one.
- We know the square root of 16, which is close: our answer should be near 4.
- Draw a picture! The picture will demonstrate two different
types of quantities that we discuss in this section:
differentials $dy$, and increments $\Delta y$.
Differentials versus increments
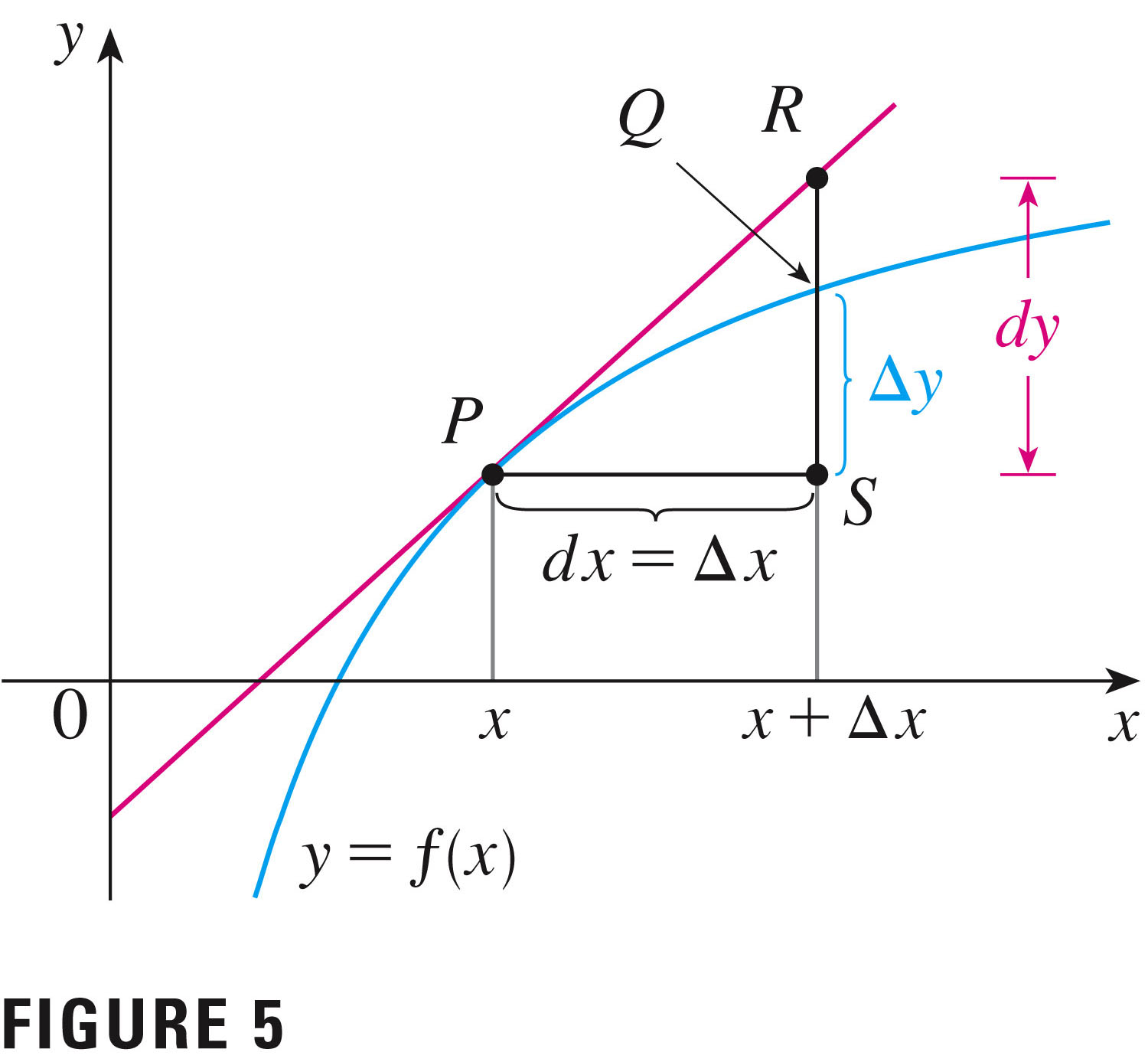
The increment is the true change in the function value; the differential approximates the true change: One way to remember the difference:- Differentials $dy$ follow the direction suggested by the derivative
- Increments $\Delta y$ are actual changes in the function value.
$dy \approx \Delta y$
We want the increment, but may settle for the easily computed differential.
- We use the tangent line for our approximation, and, when we're done, we can ask "is our answer an over- or an under-estimate?"
- We know the square root of 16, which is close: our answer should be near 4.
- Examples
- #2, p. 187
- #5
- #38
- Example application of extrema:
- The Chickens of Manitoba
- How was the flock egg production over time?
- How long should we let the flock live to maximize the average daily return?
- Maxima and minima are both types of extrema. Our author
begins by distinguishing between global (or
absolute) extrema and local extrema:
- Local is the biggest thing in the neighborhood;
- Global is the biggest thing anywhere!
- Take a moment and sketch a continuous function on the
interval [-2,2]. Make it look kind of interesting -- maybe even
ugly.
- Does your function have a global maximum and a global minimum?
- Does your function have local extrema which are not global extrema?
- If your function does have extrema, how would you characterize the derivative of the function at those extrema?
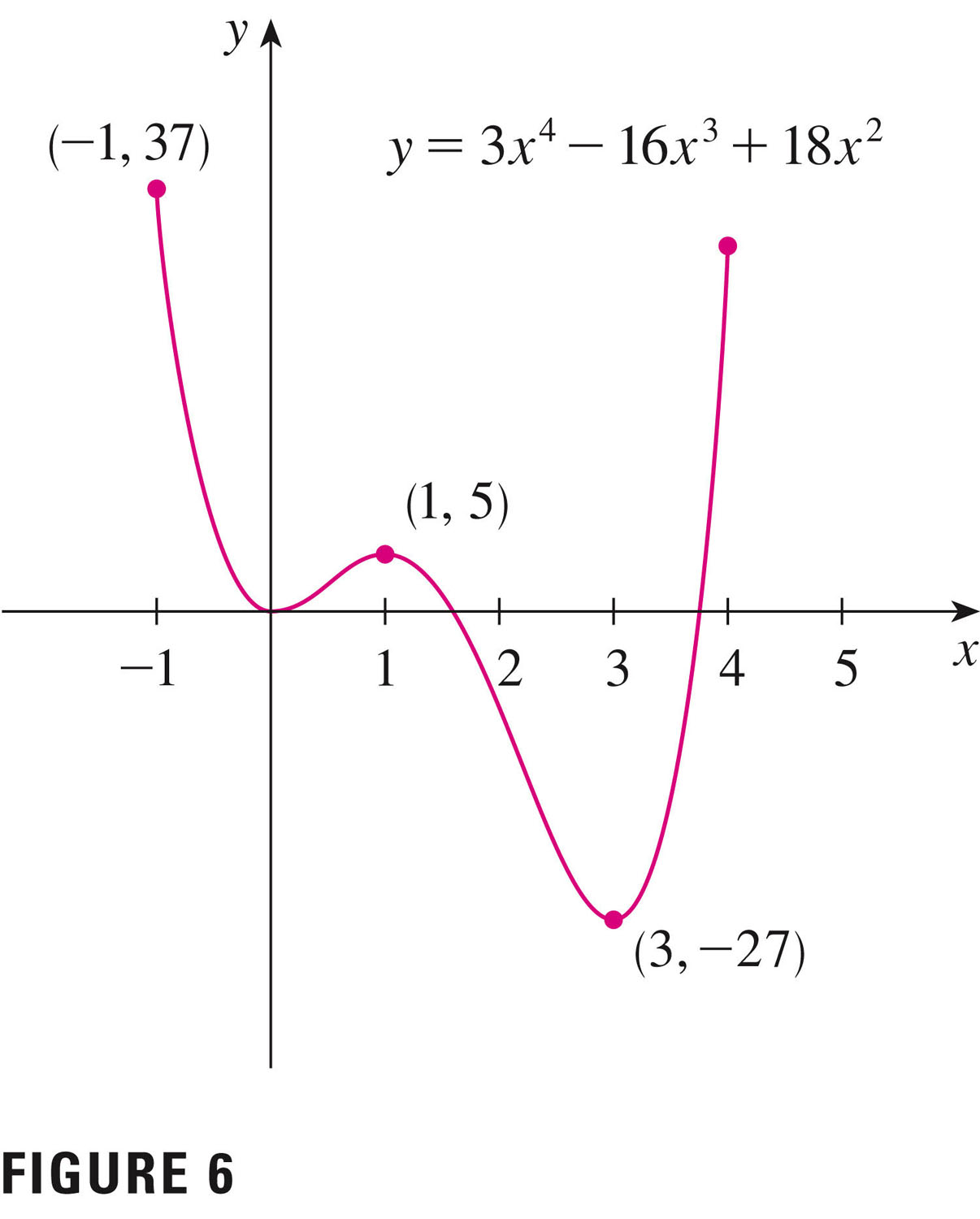
- By the way, our author requires that the function be defined in an
open interval about a local extremum. So in this figure from p. 199,
the right endpoint is not considered a local maximum:
- Now I want you to sketch a function defined on the interval [-2,2] that
does not have any global extrema. What is true about your function?
- Now I want you to sketch a smooth function on [-2,2] that has a
value of x=a where $f'(a)=0$ but no
extremum there. What is true about your function?
- By now we should have a good idea of what these two theorems say:
- Extreme Value Theorem
- Fermat's Theorem
We have hopefully deduced these:
- The Extreme Value Theorem (EVT): If $f$ is continuous on a closed interval $[a,b]$, then $f$ attains a global maximum and global minimum on $[a,b]$.
- Fermat's Theorem: If $f$ has a local max or min at $c$ and
$f^\prime(c)$ exists, then $f^\prime(c)=0$.
Rephrased: If $f$ has a local max or min at $c$, then $c$ is a critical number of $f$.
- Find the critical numbers for f (that is, those values of x at which the derivative is zero or doesn't exist).
- Find the values of f at the critical numbers of f in (a,b).
- Find the values of f at the endpoints of the interval (at a and b).
- The largest and smallest of the values from steps 1 and 2 are the absolute or global extrema.
- Now let's look at some standard problems:
- #8, p. 204
- #22
- #31, p. 205 (and let's decide whether they're local maxes or mins)
- #45 (closed interval method)
- #63
Website maintained by Andy Long. Comments appreciated.