Day 22, Mat129: Calculus I

• Your homework is returned (2.6). Graded 32, 55, 59.

• Sorry to slam you on homework just before break....:(

• Please put your rectangles away.

• Example application of extrema:
  • The Chickens of Manitoba
  • How was the flock egg production over time?
  • How long should we let the flock live to maximize the average daily return?

• Maxima and minima are both types of extrema. Our author begins by distinguishing between global (or absolute) extrema and local extrema:
  • Local is the biggest thing in the neighborhood;
  • Global is the biggest thing anywhere!

• Take a moment and sketch a continuous function on the interval [-2,2]. Make it look kind of interesting -- maybe even ugly.
  1. Does your function have a global maximum and a global minimum?
  2. Does your function have local extrema which are not global extrema?
  3. If your function does have extrema, how would you characterize the derivative of the function at those extrema?

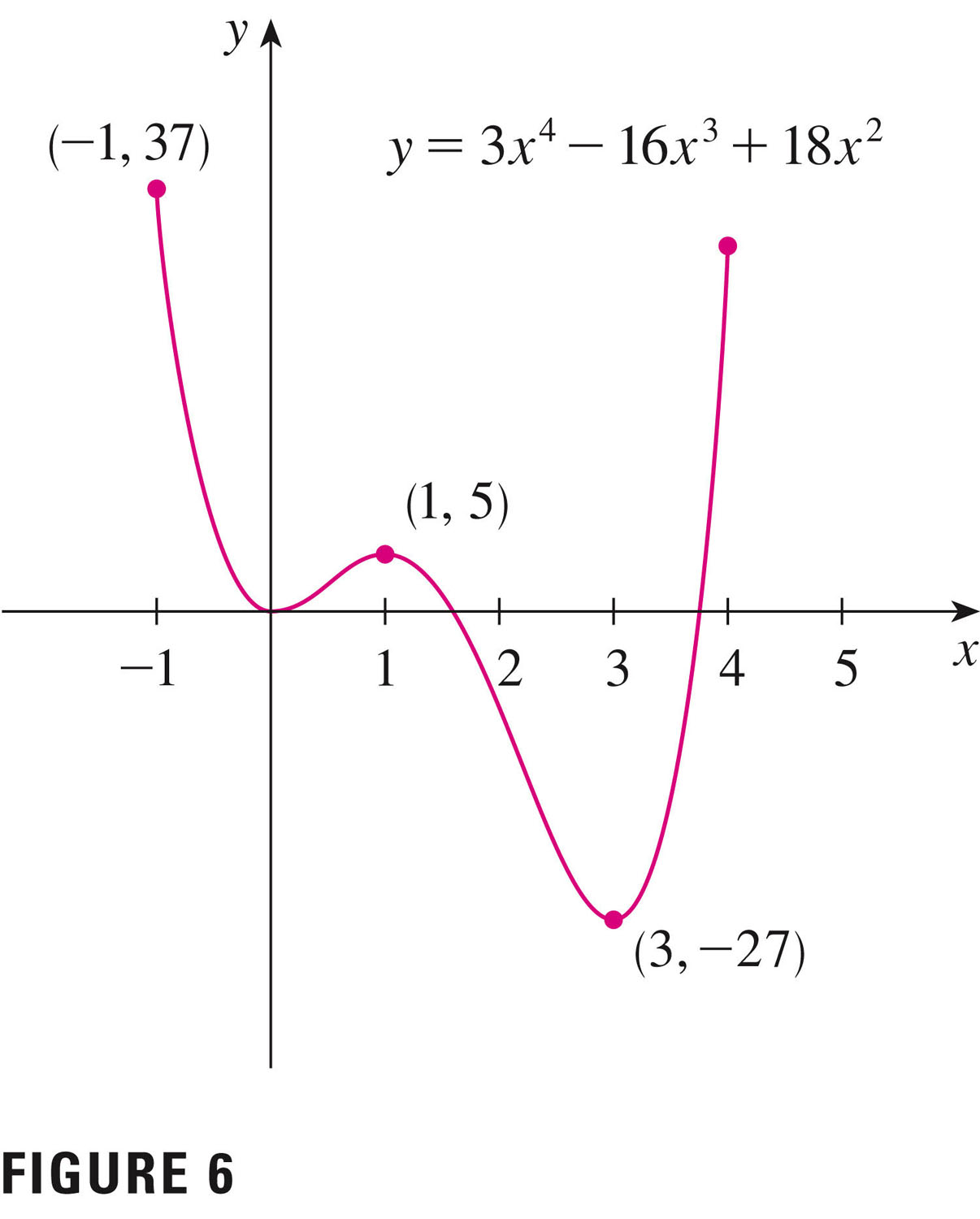
• By the way, our author requires that the function be defined in an open interval about a local extremum. So in this figure from p. 199, the right endpoint is not considered a local maximum:
  

• Now I want you to sketch a function defined on the interval [-2,2] that does not have any global extrema. What is true about your function?

• Now I want you to sketch a smooth function on [-2,2] that has a value of x=a where $f'(a)=0$ but no extremum there. What is true about your function?

• By now we should have a good idea of what these two theorems say:
  • Extreme Value Theorem
  • Fermat's Theorem

  We have hopefully deduced these:

  • The Extreme Value Theorem (EVT): If $f$ is continuous on a closed interval $[a,b]$, then $f$ attains a global maximum and global minimum on $[a,b]$.
  • Fermat's Theorem: If $f$ has a local max or min at $c$ and $f^\prime(c)$ exists, then $f^\prime(c)=0$.

    Rephrased: If $f$ has a local max or min at $c$, then $c$ is a critical number of $f$.

  We might also have deduced the closed interval method, to find the extrema of a function on a closed interval [a,b]:
  1. Find the critical numbers for f (that is, those values of x at which the derivative is zero or doesn't exist).
  2. Find the values of f at the critical numbers of f in (a,b).
  3. Find the values of f at the endpoints of the interval (at a and b).
  4. The largest and smallest of the values from steps 1 and 2 are the absolute or global extrema.

• Now let's look at some standard problems:
  • #8, p. 204
  • #22
  • #31, p. 205 (and let's decide whether they're local maxes or mins)
  • #45 (closed interval method)
  • #63

To some extent I've been pushing these ideas as we've gone along, so this should be familiar-seeming territory.

• We've already seen that derivatives are related to slopes. If the slope is positive at a point (i.e. the derivative is positive there), then the function (and its graph) is increasing there. Similarly, if the derivative is negative at a point, then the function is decreasing there.

  This is the relationship that we explore and summarize in this section. In addition, we summarize what the second derivative has to tell about the shape of a graph.

• Let's work through an example and see how the derivatives are related to the function itself. We'll need a smooth curve....

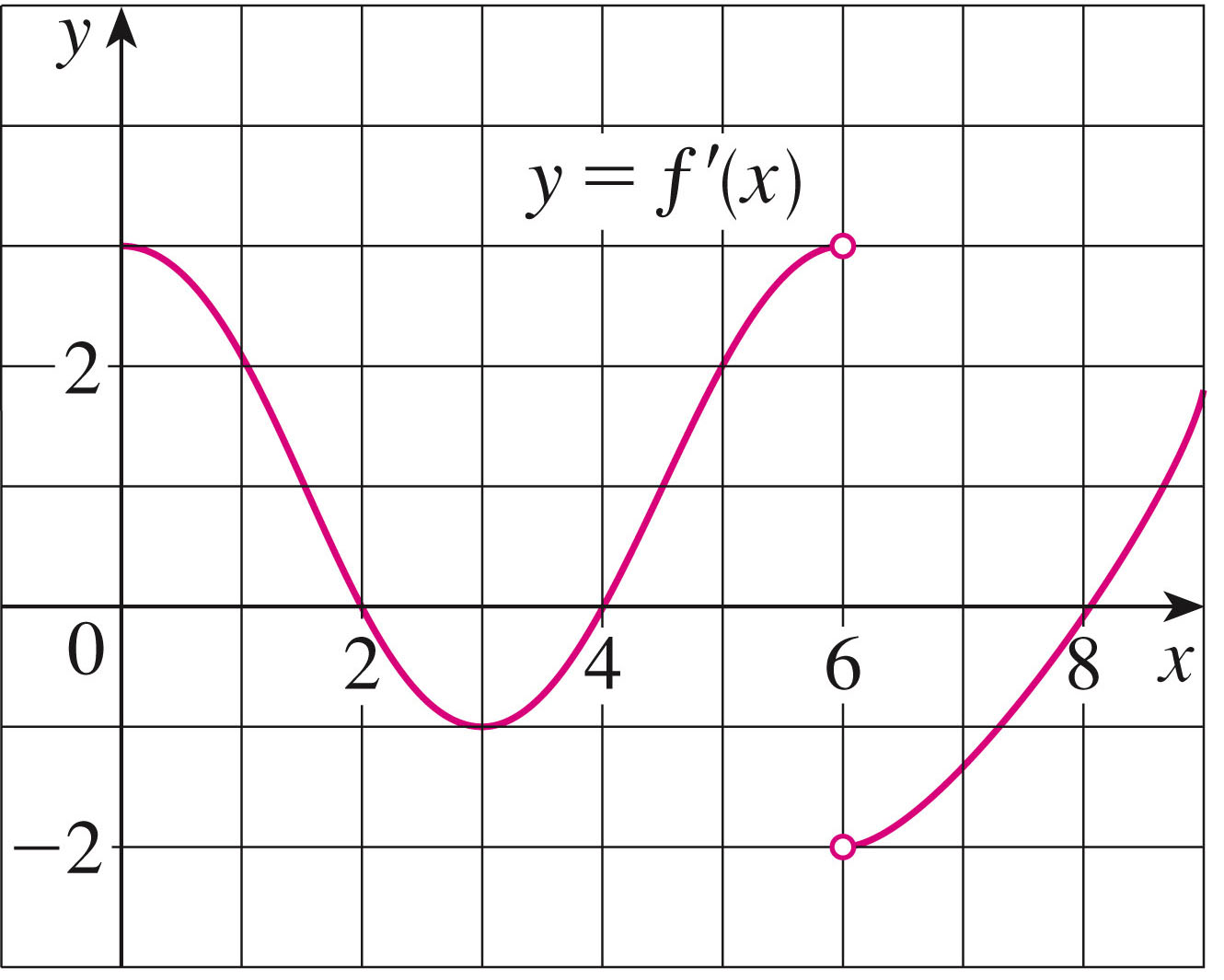
  Let's look at the graph of #5, p. 220. This is a graph of the derivative (at left):

  

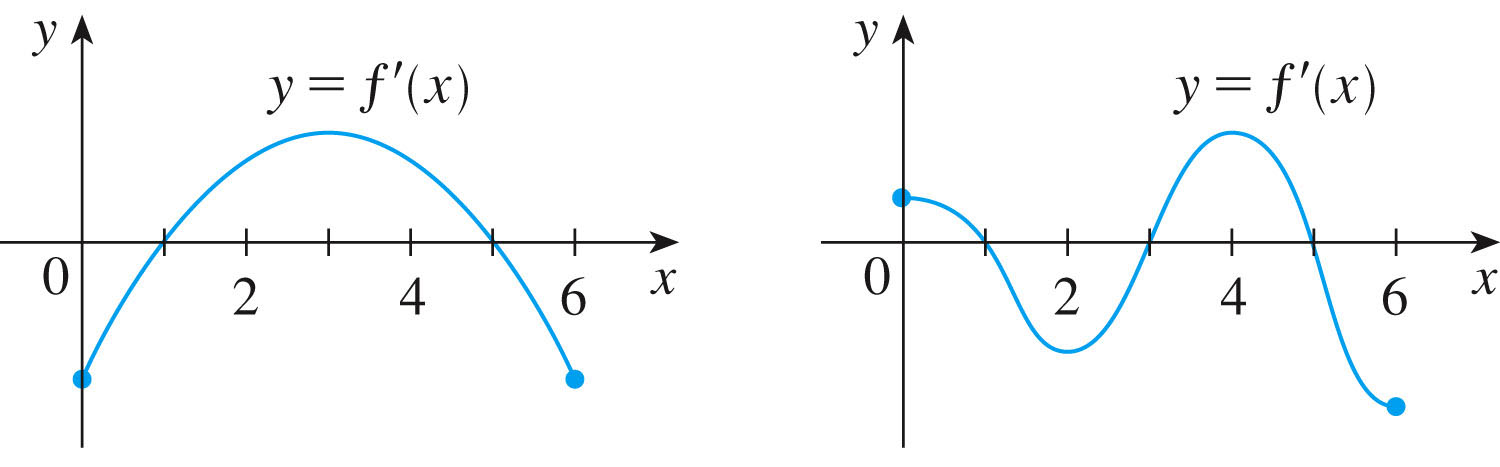
  Questions:

  1. On what intervals is $f$ increasing or decreasing?
  2. At what values of $x$ does $f$ have a local max or min?
  3. What about symmetry?
  4. What can the derivative not tell us about $f$?
  You might notice that the derivative on the left looks quadratic, and hence think to yourself that the function $f$ itself probably looks cubic....

• As we work through the example above, we should see how the first and second derivatives are related to the function itself. So doing, we discover the first and second derivative tests:
  • 1st: When a function is differentiable at a point x=a and has zero derivative (tangent line slope) there, then if the first derivative changes sign from
    • positive to negative, there's a max at x=a;
    • negative to positive, there's a min at x=a;
    • no change in sign, there's neither max nor min at x=a.

  • 2nd: When a function is differentiable at a point x=a and has zero derivative (tangent line slope) there, then if the second derivative is
    • positive at x=a, there's a min at x=a;
    • negative at x=a, there's a max at x=a;
    • zero, we're not sure what's going on....
      • $x^3$
      • $x^4$

  • If you'll just remember the two functions
    • $x^2$
    • $-x^2$
    You'll be able to keep these two rules straight.

    min	max
    $f'(x)$: - to 0 to +	$f'(x)$: + to 0 to -
    $f''(0)$: +	$f''(0)$: -

• Inflection points:
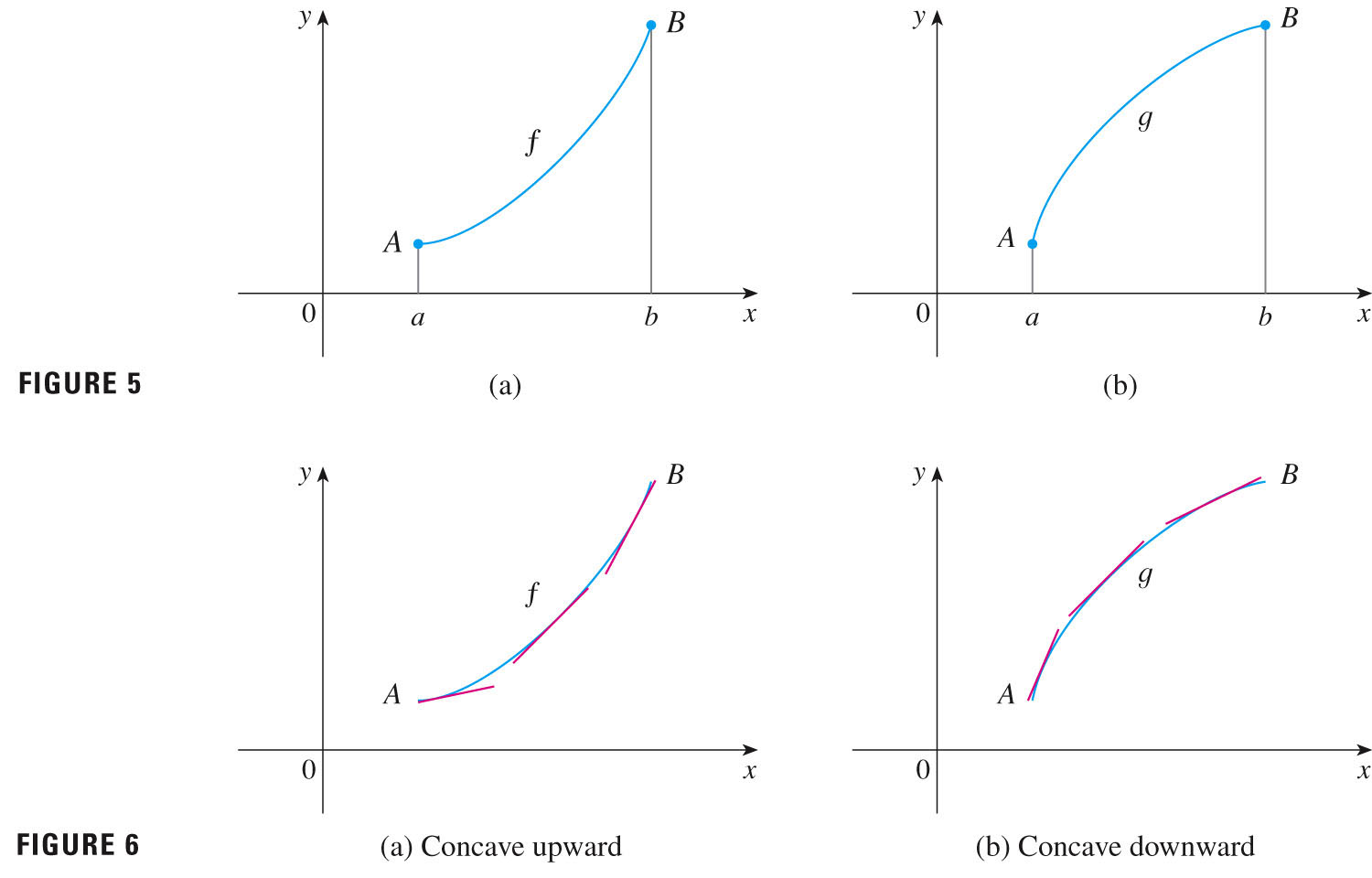
  1. A graph is concave up if it's "bowlish"; concave down if it's "umbrellaish" (see Figures 5, 6, p. 216)
     

  2. inflection point: Point P on a curve is an inflection point if the curve changes concavity at P.
  3. ``There is a point of inflection at any point where the second derivative changes sign.'' (p. 218)

     This figure is from Example 5, p. 218:

     

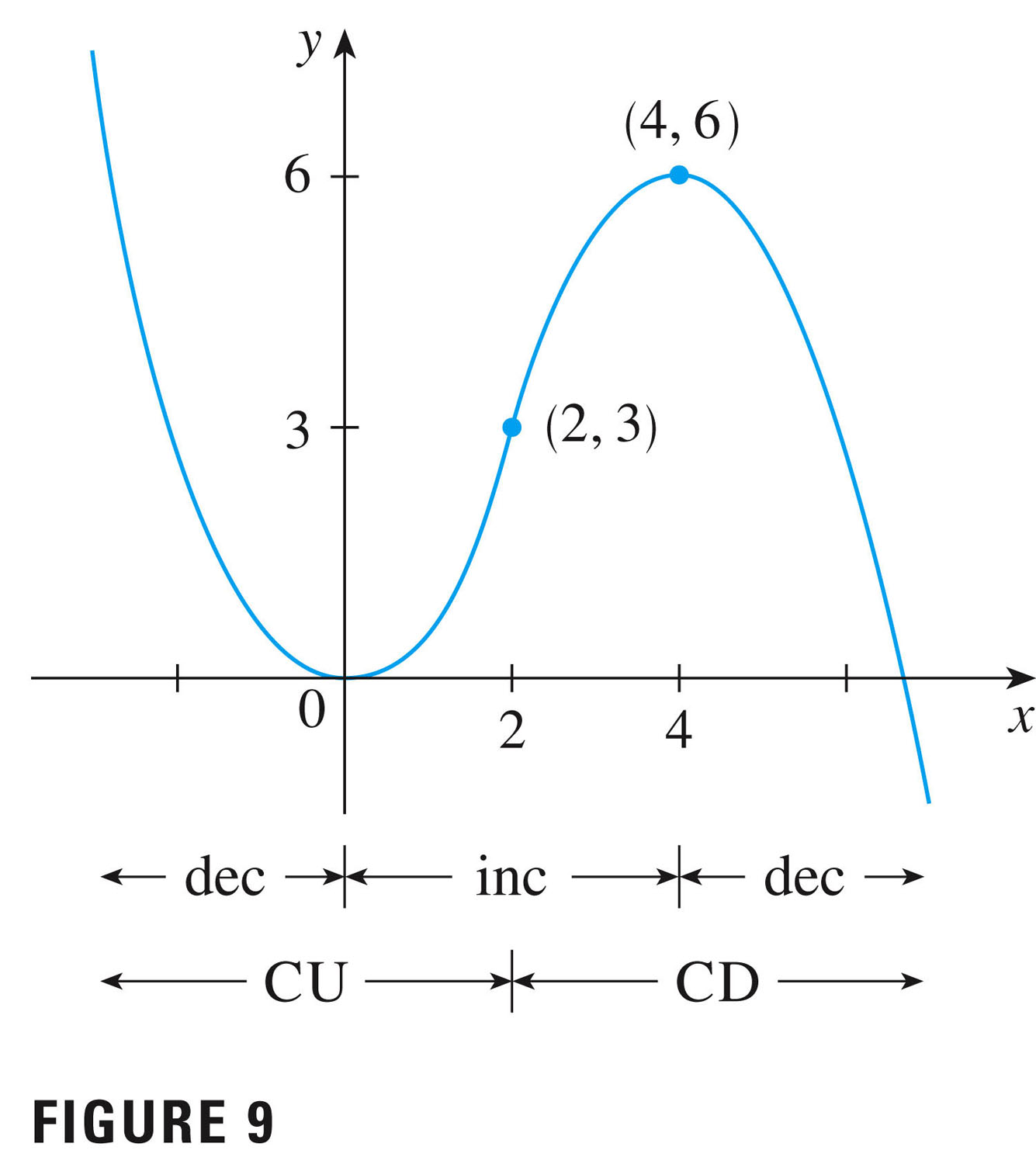
     You might notice that the function itself looks cubic, and hence think to yourself that the derivative probably looks quadratic....

• Examples:
  • #6, p. 220
    

  • #27
    

  • #23
  • #39
  • #50
  • #51