- Your exam revisions are due today.
- You have a homework due today.
- Your quiz is returned.
It's time, however, to go back to the dashboard: we're not focused on finding speeds from changes in distance now, but rather we're going to focus on the odometer: how do tell how far we've travelled given a history of our speeds? Back to Day02:
The big ideas of Calc I are contained in Gil Strang's "Auto Analogy": he says that the "The central question of calculus is the relation between [speed and distance traveled]."
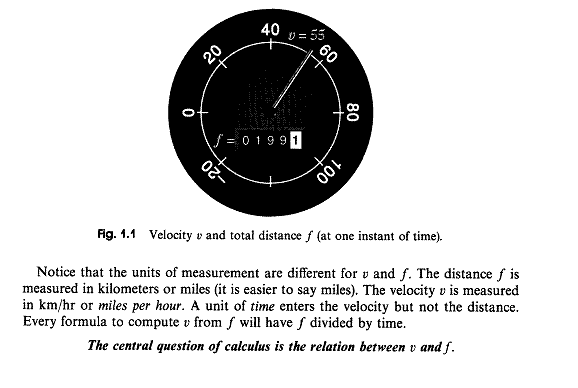
Imagine that the car is operated on a long, straight road. (Just for the sake of convenience, we won't allow it to travel in reverse! Otherwise we'd be talking about velocity -- speed and direction -- rather than just speed.)
- Suppose that you clock your speed
at each minute along a trip, in mph:
minute 0 1 2 3 4 5 6 7 8 9 10 speed (mph) 0 30 45 30 70 65 70 70 45 30 35 Estimate the distance travelled.
- Use Dirt! If you were going at a constant rate of speed, you could
use the ol' dirt formula:
\[
d=r*t
\]
where $r$ is the speed of travel,
and by $t$ we mean the duration of the motion.
- If you're traveling at a constant speed, then your work is done: d=r*t.
- If not, then we could imagine that for each short time segment,
the given speed is fixed. This leads to a discontinuous speed
function. But it's easy to estimate the total distance
travelled: it's just a bunch of mini dirt calculations.
- One thing for sure: if we do that, since we're dealing with
sampled data, we're probably wrong -- but we can hope that
we're close, especially if we sample frequently enough.
- Ideally we'd know the speed at any moment. As a pretention of
that, we might fit straight line segments between data
points, and suppose that that's the continuous speed
function.
This strategy gives rise to the so-called "Trapezoidal rule", which we'll encounter in a moment.
Last time we did a "thought experiment", about traveling down a straight road in different ways:
- at a constant speed;
- at two different speeds; and
- at a continously varying speed.
If we were going a constant speed, then everything is easy:
\[ D(b)=p'(0)(b-0) = p(b)-p(0) \]
We also noticed that this is equal to the area under the rectangle formed by the speed function (a constant, say 5 mph):
If you walk 5 mph, then in two hours you will walk 10 miles: $5\frac{miles}{hour}*2hours=10$ miles.
If we sample the speed at $n$ equally spaced moments $t_i$ (like your black box does!), then we discovered that we could estimate the displacement, or distance travelled, as a sum:
\[ D(b)=\sum_{i=0}^{n-1}p'(t_i)\Delta t \]
where we use "summation notation" to represent a sum of terms, with $i$ running from 0 to $n-1$ (notice that gives $n$ values of $i$, and hence $n$ subintervals).
$\Delta t = \frac{b}{n}$ is the length of an interval (in your black box this might be every hundredth of a second).
Now it's true that \[ D(b)=\sum_{i=0}^{n-1}p'(t_i)\Delta t \approx p(b)-p(0) \] Now if we want to get this exactly right, and replace that $\approx$ with an equals sign, we need to continue to subdivide the interval more finely; in fact, we must subdivide so finally that we let $\Delta t \to 0$ (or, alternatively, we let $n \to \infty$):
\[ D(b)=\lim\limits_{n \to \infty}\sum_{i=0}^{n-1}p'(t_i)\Delta t = p(b)-p(0) \]
Finally we introduced notation for that horrible limiting sum on the left: we used integral notation, and wrote (more cleanly)
\[ D(b)=\int_{0}^{b}\ p'(t)\ dt = p(b)-p(0) \]
where the integral sign $\int$ is thought of as an elongated S, for "sum" (only we're adding up an infinite number of infinitesimally small rectangles (there's a word for you, a big word for a very small thing!!)).
The rectangles have a real, finite height $p'(t)$, but their width has gone to zero, but in such a way that they remain... well... like pixie dust, let's say!:) So we call the width $dt$ an infinitesimal.
You've actually seen this before: in \[ \frac{df}{dt}=\lim\limits_{dt\to 0}\frac{f(t+dt)-f(t)}{dt} \]
$dt$ has been going to zero for quite some time, and it never quite gets there -- but it's smaller than any real number. You know -- pixie dust!
- If you're traveling at a constant speed, then your work is done: d=r*t.
- Areas
So now we recast our problem as one of computing areas -- but we won't forget our amazing result, that the distance travelled (the odometer reading) can be determined from the speed (ometer): if you know your rate of change at every moment, then you can figure out your position.
We noticed last time that the choice of the speed was a little arbitrary: why do we use the speed at the left of the interval in time to make our estimates of the distance travelled?
We could just as easily have taken an estimate at the end of an interval, leading to what we call the "right rectangle rule":
\[ D(b)=\sum_{i=1}^{n}p'(t_i)\Delta t \approx p(b)-p(0) \]
It looks a lot like the other rule, only $i$ is running from 1 to $n$, and to the $t_i$ sample are right endpoints, not left endpoints.
So let's have a look at several different "integration rules", and how they relate to one another.
There are several useful rectangular rules, such as Left/Right/Midpoint rules:
- Estimates for the given data:
- RRR (Right Rectangle Rule): d = 45.5*10 mph*minutes = 7.58 miles
- LRR (Left Rectangle Rule): d = 49*10 mph*minutes = 8.17 miles
- Trapezoidal rule = 47.25*10 mph*minutes = 7.88 miles
- Notes:
-
- Whenever you have two estimates, you have a third:
- the trapezoidal rule is the average of left and right rectangle rules.
- Each of these estimates corresponds to computing a rectangle height (an
average speed), and then multiplying by the total time (10
minutes). Hence we're using the "dirt" formula, and computing the
average (the "area under the curve", even though there's no curve!) in
several different ways.
- Basically, every function can be used to create a table like this, and
then we can use these strategies.
- Example:
- Often (as in the table above) we have data located at equal intervals ($\Delta{x}$). When you have a curve (or a formula) for $f$, you can take the time
intervals shorter and shorter, until you get as close to the area as you
need:
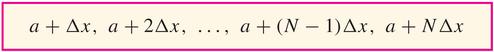
(notice that $a+N\Delta{x=b}$ that is, that $\Delta{x}=\frac{b-a}{N}$)
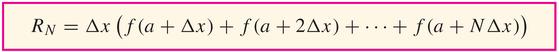
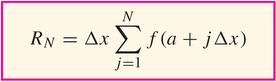
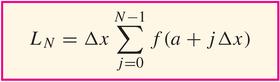
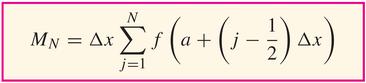
Then, in fact,

- Examples:
- #1, p. 293
- Generalizations?
- The area can be calculated by finding an average value on the
interval, times the length of the interval:
Area under the graph of $f$ from $a$ to $b$ = $\bar{f}(b-a)$ where by $\bar{f}\mbox{}$ we mean an average value of $f$.
- The area can be calculated by chopping the interval $[a,b]$
up into smaller and smaller chunks, and then using rectangular approximations
to the small areas.
- In our work so far, the intervals into which the interval is chopped have been equal-sized: no reason to stick with that.
- If the size of the intervals goes to zero, then the approximations get better and better, until they're perfect!
- The area can be calculated by finding an average value on the
interval, times the length of the interval:
- Some more examples:
- #6
- #15
- Estimates for the given data: