- Your homework 3.7 is returned: graded 19 and 28.
- Your homework 3.9 is due today.
- section 4.1 -- areas and distances
- section 4.2 -- The definite integral
- section 4.3 -- The fundamental theorem of calculus
- LRR (above)
- RRR: $\sum_{i=1}^{n}p'(t_i)\Delta t$
- Whenever you have two estimates, you have a third:
so we also defined the trapezoidal rule is the average of left and right rectangle rules:
TRAP: $\frac{LRR + RRR}{2}$
- Midpoint: $\sum_{i=1}^{n}p'(t_i-\frac{1}{2}\Delta t)\Delta t$
Each of these estimates corresponds to computing a rectangle height (a "representative" or average speed for that interval), and then multiplying by the total time. Hence we're using the "dirt" formula, and computing the average (the "area under the curve", even though there's no curve!) in several different ways.
If we take the limit as $n \to \infty$ (that is, drive $\Delta t=\frac{b}{n} \to 0$), then we get the exact distance (which is equivalent to an area), and represent it with this integral notation: \[ p(b)-p(0)=\int_{0}^{b}p'(t)dt \]
This is called a definite integral, because the limits of integration (0 and $b$) are fixed (definite). In the near future we will be relaxing that, and allowing "indefinite" limits.
Generalizations?
- We know that we can calculate an average speed $\overline{s}$ for a trip, so that \[ p(b)-p(0)=\int_{0}^{b}p'(t)dt = \overline{s}b \]
- Similarly the area under a curve (and above the $x$-axis) can be
calculated by finding an average value on the interval, times the length of the
interval:
Area under the graph of $f$ from $a$ to $b$ = $\bar{f}(b-a)$ where by $\bar{f}\mbox{}$ we mean an average value of $f$.
- The area can be calculated by chopping the interval $[a,b]$
up into smaller and smaller chunks, and then using rectangular approximations
to the small areas.
- In our work so far, the intervals into which the interval is chopped have been equal-sized: no reason to stick with that.
- If the size of the intervals goes to zero, then the approximations get better and better, until they're perfect!
- Some more examples:
- #1, p. 293
- #6
- #14, p. 294
- #15
- This section generalizes our intuition and examples from the preceding section:
- First of all, we can't expect our function to be positive all the time, so
we define "signed area":

and then we give a name to this area:

- Just FYI: the area can be calculated by chopping the interval [a,b]
up into smaller and smaller chunks, and then using rectangular approximations
to the small areas.
- In our work so far, the intervals into which the interval
is chopped have been equal-sized: no reason to stick with that (although we
will in this course). So, more generally, we define the Riemann
sum as
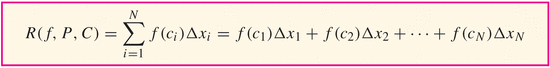
where P is called a partition of the interval $[a,b]$:
$a=x_0 \lt x_1 \lt x_2 \lt \ldots \lt x_N=b$ and where C is a set of intermediate points $C={c_1,\ldots,c_N}$ such that
$c_i\in[x_{i-1},x_i]$ - If the size of the intervals goes to zero, then the
approximations get better and better, until they're perfect!

where
$\|P\|$ is the width of the largest subinterval,$max(\{\Delta{x_i}|i\in\{1,\ldots,N\}\})$ for the partition.
- In our work so far, the intervals into which the interval
is chopped have been equal-sized: no reason to stick with that (although we
will in this course). So, more generally, we define the Riemann
sum as
- Properties of the Definite Integral:



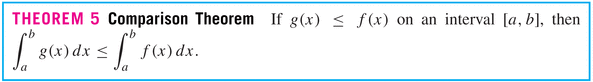
- Examples:
- #7, p. 306
- #10
- #21
- #33
- #41 (sort of a trick question...)
- #42
- #48
- #57
- First of all, we can't expect our function to be positive all the time, so
we define "signed area":
- Well folks, here it is: the fundamental theorem, that ties together integral and differential calculus. It comes in two parts:
-
If $f$ is continuous on $[a,b]$, then
$\int_{a}^{b}f(x)dx=F(b)-F(a)$ where $F$ is any antiderivative of $f$; that is, a function such that $F'=f$. - If $f$ is continuous on $[a,b]$,
then the function $g$ defined by
$g(x)=\int_{a}^{x}f(t)dt \;\;\;\;\; a \le x \le b$ is continuous on $[a,b]$ and differentiable on $(a,b)$, and $g'(x)=f(x)$.
-
- We've already derived this once: here's a slightly different take
on it, incorporating both parts I and II of the theorem: derive/motivate the FTC using the linearization.
- Examples:
- #3, p. 318
- #8
- #13 (a composition, requiring the chain rule)
- #22
- #23
- #58