- We'll have a quiz at the end of the hour.
- Your second exams are returned.
Some of you must redo a problem or two before your score will be changed. Please get those to me ASAP.
A few points:
- Learn your basic rules. Still seeing some sign errors on quotient rules.
- Lots of over-dependence on the key on problem 2:
\[
p'(x)=\lim\limits_{h\to 0}\frac{p(x+h)-p(x)}{h}
\]
should be your first line, and was in almost no case.
In part b.: the EVT requires continuity, not differentiability; but differentiability implies continuity.
- Seeing some unit issues still. Units are a challenge, but also an opportunity to spot errors.
- I continually recommend that you stop using the
slope-intercept form for tangent lines: the better form is
point-slope.
Keep slopes exact, if you can -- leave approximations to the user. So the exact slope is $\frac{-1}{\sqrt{3}}$, which you find either explicitly or implicitly.
- You're still struggling with long division to get the precise asymptotic behaviour. Also most of you didn't do part c. correctly: you need to complete the square.
- Again, in overdependence on the key, most of you now draw only half the graph. I am not at all sure that some of you know how to draw the other half. You didn't indicate that the function is odd, and hence that the other half may be obtained by rotating the curve on the right around the origin by 180 degrees.
- Avoid comical adherence to a key.
On Problem 7, some of you left a big hole in a rational function's graph -- because the graph was so faint on the key that you thought it wasn't there.
It made me sad:(. You clearly don't understand rational functions if you do that. Some of you also wrote "odd", but then your graph is clearly not odd. So there's a serious adherence to nonsense going on there.
Think independently, and have the courage of your convictions.
- Your homework 3.9 is not returned: graded 29 and 56
- Your homework 4.1 is due today.
- section 4.2 -- The definite integral
- section 4.3 -- The fundamental theorem of calculus
- This section generalizes our intuition and examples from the preceding section:
- First of all, we can't expect our function to be positive all the time, so
we define "signed area":

and then we give a name to this area:

- Just FYI: the area can be calculated by chopping the interval [a,b]
up into smaller and smaller chunks, and then using rectangular approximations
to the small areas.
- In our work so far, the intervals into which the interval
is chopped have been equal-sized: no reason to stick with that (although we
will in this course). So, more generally, we define the Riemann
sum as
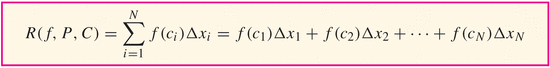
where P is called a partition of the interval $[a,b]$:
$a=x_0 \lt x_1 \lt x_2 \lt \ldots \lt x_N=b$ and where C is a set of intermediate points $C={c_1,\ldots,c_N}$ such that
$c_i\in[x_{i-1},x_i]$ - If the size of the intervals goes to zero, then the
approximations get better and better, until they're perfect!

where
$\|P\|$ is the width of the largest subinterval,$max(\{\Delta{x_i}|i\in\{1,\ldots,N\}\})$ for the partition.
- In our work so far, the intervals into which the interval
is chopped have been equal-sized: no reason to stick with that (although we
will in this course). So, more generally, we define the Riemann
sum as
- Properties of the Definite Integral:



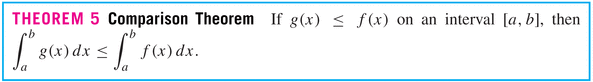
- Examples:
- #7, p. 306
- #10
- #21
- #33
- #41 (sort of a trick question...)
- #42 (reversing the order of integration, dummy variable of integration)
- #48
- #57
- First of all, we can't expect our function to be positive all the time, so
we define "signed area":
- Well folks, here it is: the fundamental theorem, that ties
together integral and differential calculus. It comes in two parts:
-
If $f$ is continuous on $[a,b]$, then
$\int_{a}^{b}f(x)dx=F(b)-F(a)$ where $F$ is any antiderivative of $f$; that is, a function such that $F'=f$. - If $f$ is continuous on $[a,b]$,
then the function $g$ defined by
$g(x)=\int_{a}^{x}f(t)dt \;\;\;\;\; a \le x \le b$ is continuous on $[a,b]$ and differentiable on $(a,b)$, and $g'(x)=f(x)$.
Note the only essential condition:
- $f$ is continuous on $[a,b]$.
Have a look at Example 8, p. 316.
-
- We've already derived this once (at least half of it): here's a slightly different take
on it, incorporating both parts I and II of the theorem: derive/motivate the FTC using the linearization.
- Examples:
- #3, p. 318
- #8
- #13 (a composition, requiring the chain rule)
- #16
- #22
- #23
- #34
- #58