- I hope that you had a good holiday.
- Your quizzes are graded and returned.
- Quiz 1 mean: 9.7
- A nice solution (there were several 11s...)
- Please label your axes when plotting. A few numbers along each axis really helps!
- A reminder that you'll get two drops.
- Last time we had our first lab, and I hope that you felt okay
about it. We'll continually add new techniques each week. We
we started learning how to do these things with Mathematica:
- think about what constitutes a function, and find some data representing functions
- Plot functions
- Define functions
- Manipulate functions (with the Manipulate command)
- and Model with functions
- You will have a quiz Thursday, over inverses.
We're on to Vol 1, Sec 3.7: Derivatives of Inverse functions
We'll approach this topic via several examples, making good use of the chain rule:
- Let's begin with the very simplest example, a pair of linear
functions which are inverses of each other and which are really
important (because different nations use different temperature
systems, we frequently have to translate between these two
systems -- at least I do, in Canada, where I live for half of
the year).
- These inverse functions have a nice symmetry about the mirror line $F=C$:
they're reflections about the line. (Where do they intersect?)
- The slopes of the two lines are multiplicative inverses of each
other.
- If the point $(x,y)$ appears on one graph, then the point $(y,x)$
will appear on the other graph. (This just restates the first
observation!)
- One function is written as though \(F\) is the independent variable (on the
\(x\)-axis), whereas the other is written as though \(C\) is the
independent variable.
Notice that the equation \(F=T(C)\) is written in slope-intercept form, whereas the equation \(C=T^{-1}(F)\) is written in point-slope form.
Why does this make sense in this particular case, of these two temperature scales?
- Here is an example of where you definitely don't want to "switch \(x\) and \(y\)" before you compute the inverse -- because you'll get nonsense out of one of the formulas!
- These inverse functions have a nice symmetry about the mirror line $F=C$:
they're reflections about the line. (Where do they intersect?)
- This example is important because it generalizes: tangent lines at
corresponding points on graphs of \(f\) and \(f^{-1}\) have slopes
which are inverses of each other, too:
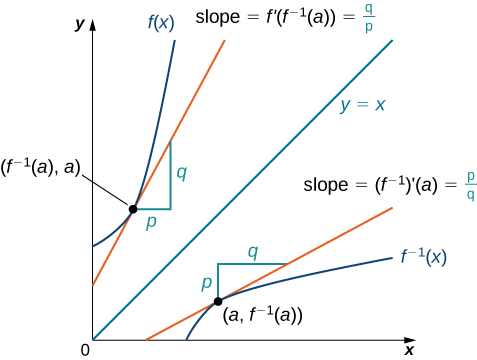
We might look at how this plays out in problem 266, for example.
- We now move on to a nice, friendly polynomial: $x^2$
- Inverse functions undo the work of their function
partners. Probably one of the first inverse functions you encountered
in your mathematical career is the square root and its partner the
square. We will denote the function and its inverse this way: if the
square function is called $f$, then its inverse will be called
$f^{-1}$:
(WARNING: don't be fooled by the notation: $f^{-1}(x)$ is the inverse function; $f(x)^{-1}$is the multiplicative inverse, $\frac{1}{f(x)}$. They are completely different animals!)
\[ f(x)=x^2 \] and \[ f^{-1}(x)=\sqrt{x} = x^{\frac{1}{2}} \]
This is an interesting place to start, because the square function isn't actually invertible!
By convention, we restrict the domain, and choose to consider the square function on only half of its domain (positive values of $x$).
- Note that the portion of the square function to the right of the
$y$-axis, and the square root function are just reflections of each
other about the line $y=x$. This is always the case for inverse
functions.
And you can see what goes wrong if we try to reflect the part to the left of the $y$-axis: the inverse "function" would fail the vertical line test -- very naughty "function".
- The important power of inverse functions is that they "undo" each
other. This is expressed as follows, where \(f(x)=y\) is invertible:
\[
f^{-1}(f(x)) = x
\]
and
\[
f(f^{-1}(y)) = y
\]
It's unfortunate that we, being lazy mathematicians, will typically use \(x\) as the variable in both of these formulas (as we see in this picture):
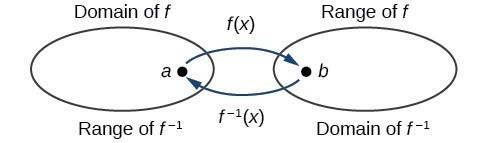
But we need to remember that \(f^{-1}\) operates on the range of f, \(R_f\), that is on the values of \(y=f(x)\), and takes them back to the domain of \(f\).
- We now show that it's possible to figure out the derivative of the
square root function without using the power rule for fractional
powers.
We begin by observing that \[ f(x)=x^2 \] \[ f^{-1}(y)=\sqrt{y}. \] and \[ f(f^{-1}(y))=y. \]
We assert that if the two functions are equal, then their derivatives must be equal as well (does that make sense?). So let's differentiate with respect to \(y\):
\[ \frac{d}{dy}\left(f(f^{-1}(y))\right) = \frac{d}{dy}(y) \] Then, using the chain rule on the left, \[ f'(f^{-1}(y)) \frac{d}{dy}\left(f^{-1}(y)\right) = 1 \] So \[ \frac{d}{dy}\left(f^{-1}(y)\right) = \frac{1}{f'(f^{-1}(y))} \] This is the key result, summarized in Theorem 3.11, where the same result is written in terms of the variable \(x\):

One other thing that they do in their theorem is give the name of \(g\) to \(f^{-1}\) -- not a bad idea, since that notation is so egregious.
Let's do an example: for $f(x)=x^2$, $f'(x)=2x$: so \[ f'(f^{-1}(y))=2f^{-1}(y) \] and \[ \frac{d}{dy}\left(f^{-1}(y)\right) = \frac{1}{2f^{-1}(y)} = \frac{1}{2\sqrt{y}} = \frac{1}{2}y^{-\frac{1}{2}} \] Re-written in terms of \(x\), where we're more familiar, we say that
\[ \frac{d}{dx} \left( f^{-1}(x) \right) = \frac{d}{dx} \left( \sqrt{x} \right) = \frac{d}{dx} \left(x^{\frac{1}{2}}\right) = \frac{1}{2}x^{-\frac{1}{2}} \] Just as we suspected!
- Inverse functions undo the work of their function
partners. Probably one of the first inverse functions you encountered
in your mathematical career is the square root and its partner the
square. We will denote the function and its inverse this way: if the
square function is called $f$, then its inverse will be called
$f^{-1}$:
- One more important example
considered in this section: the inverse function of
$f(x)=\sin(x)$: we'll call it $f^{-1}(x)=\arcsin(x)$.
- Just as before, but once again we have to restrict the domain:
sine is not invertible. We have a choice, but it seems like the best
place to think of sine as invertible is on the interval $[-\frac{\pi}{2},\frac{\pi}{2}]$:
- Now how about its derivative?
This example I'll switch back to using \(x\) as the independent variable, just because we're a little more comfortable with that.
There will be enough other stuff to make us uncomfortable....:)
For $f(x)=\sin(x)$, $f'(x)=\cos(x)$ -- easy! But this time it will be a little more unpleasant to compute \[ f'(f^{-1}(x)) = \cos(\arcsin(x)). \]
There's a trick you know, however: we can rewrite cosine in terms of sine, using our most important trig identity: \[ \sin(x)^2+\cos(x)^2=1, \] so \[ \cos(x)=\pm\sqrt{1-\sin(x)^2}, \] Hence \[ \frac{d}{dx}\left(f^{-1}(x)\right) = \frac{1}{\pm\sqrt{1-\sin(\arcsin(x))^2}} \] becomes \[ \frac{d}{dx}\left(\arcsin(x)\right) = \frac{1}{\sqrt{1-x^2}} \] where you will notice that I chose the positive "branch". Why?
Look at sine on this interval. If it is increasing everywhere, its inverse must be increasing everywhere: and what does that say about its derivative?
- Just as before, but once again we have to restrict the domain:
sine is not invertible. We have a choice, but it seems like the best
place to think of sine as invertible is on the interval $[-\frac{\pi}{2},\frac{\pi}{2}]$:
- Your turn!
There are two other functions which deserve our attention. We call their inverses "arctan" and "arccos".
Do exactly the same thing that we've just done in these three examples, but with two other important functions:
- $f(x)=\cos(x)$ -- use restricted domain $[0,\pi]$
Observe that we could compute this derivative using a transformation: we've already observed that \[ \arccos(x)=\frac{\pi}{2}-\arcsin(x) \]
\[ \arccos'(x)=-\arcsin'(x) \]
- $f(x)=\tan(x)$ -- use restricted domain $(-\frac{\pi}{2},\frac{\pi}{2})$
- $f(x)=\cos(x)$ -- use restricted domain $[0,\pi]$
- For a different take: Active Calculus, Section 2.6: Inverse functions and their derivatives
- Another Mathematica file, to review the shapes of basic functions, and some of their properties.
- Here's some Mathematica showing the Ceiling And Floor functions at work, to solve the Checkpoint 1.15 problem about postal rates.