- We'll have a quiz at the end of the hour over inverse functions.
We're on to Vol 1, Sec 3.9: Derivatives of exponential and logarithmic functions
- Any questions about homework problems?
- Last time we were studying the relationship between the
derivatives of \(f\) and \(f^{-1}\): they reflect each other in
the mirror of \(y=x\), as in this example, as do their tangent
lines at corresponding points \((a,b)\) and \((b,a)\):
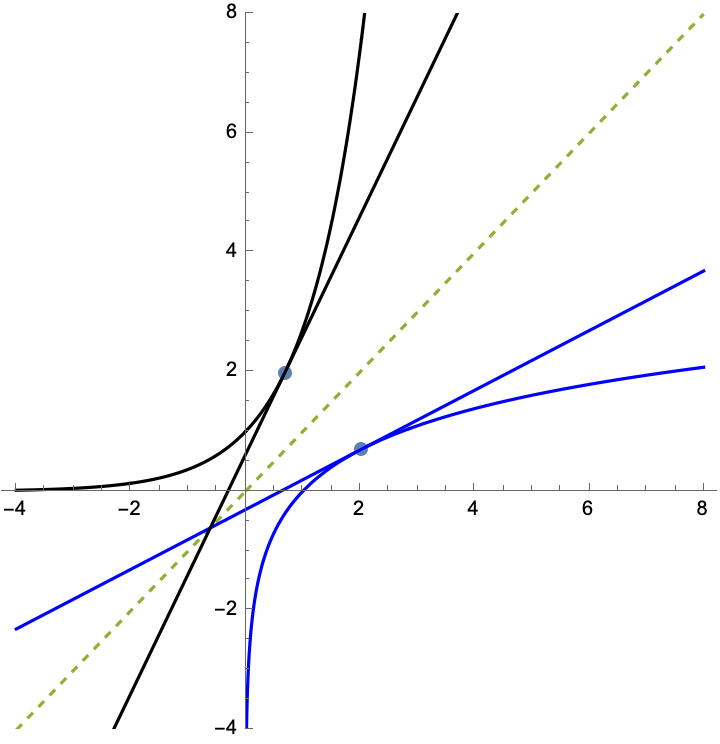
The slopes of those tangents are multiplicative inverses: if the slope of one is \(m\), the slope of the other is \(\frac{1}{m}\).
- As mentioned last time, the important power of inverse functions
is that they "undo" each other. This is expressed as follows, where
\(f(x)=y\) is invertible:
\[
f^{-1}(f(x)) = x
\]
and
\[
f(f^{-1}(y)) = y
\]
- The key result, summarized in Theorem 3.11, where the same result is
written in terms of the variable \(x\):

- The most important example we want to consider today is the
inverse function of $f(x)=e^x$: we'll call it $f^{-1}(x)=\ln(x)$.
- We're going to proceed exactly as we did before, only this time
we're in luck: the function $f(x)=e^x$ is, in fact, invertible -- no
need to restrict a domain!
- The derivative of $f(x)=e^x$ will be required, and you may already
know it: $f'(x)=e^x$. But how do we get that? Via the most beautiful
idea in calculus, the limit definition:
\[ f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h} \] Thus \[ f'(x)=\lim_{h \to 0}\frac{e^{x+h}-e^x}{h} \] Using a property of exponentials in general, \[ f'(x)=\lim_{h \to 0}\frac{e^{x}e^{h}-e^x}{h}=\lim_{h \to 0}\frac{e^{x}(e^{h}-1)}{h} \] And, since \(e^{x}\) is independent of \(h\), we can pull it out from under the limit: \[ f'(x)=e^{x}\lim_{h \to 0}\frac{(e^{h}-1)}{h}=e^{x}\lim_{h \to 0}\frac{(e^{h}-e^{0})}{h}=e^{x}\lim_{h \to 0}\frac{(e^{0+h}-e^{0})}{h} \] But \[ \lim_{h \to 0}\frac{(e^{0+h}-e^{0})}{h} = f'(0) \] and thus \[ f'(x)=e^{x} f'(0) \] i.e. the derivative of an exponential function generally is proportional to itself, with a constant of proportionality equal to the slope of the tangent line at \(x=0\).
The value of \(e \approx 2.718281828459045\) is actually chosen because \(e\) is the particular base whose derivative at \(x=0\) is 1:
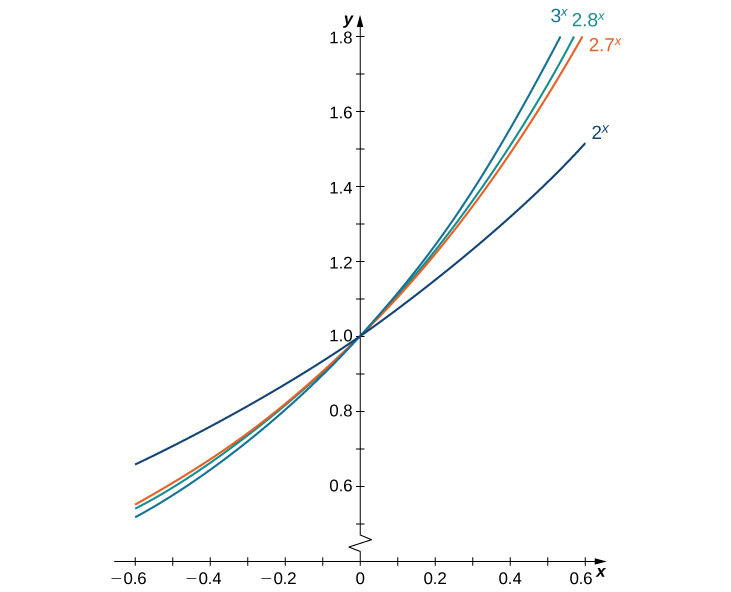
Thus \(f'(x)=e^{x}=f(x)\). This is a really incredible property!
It means that the second derivative is also \(f(x)\), and third, and fourth, and ....
- Now we're ready to move on to derivative of the inverse. We have
$f(x)=e^x$, $f^{-1}(x)=\ln(x)$, $f'(x)=e^x$: let's apply the rule!
So \[ \frac{d}{dx}\left(f^{-1}(x)\right) = \frac{1}{f'(f^{-1}(x))} \] becomes \[ \frac{d}{dx}\left(\ln(x)\right) = \frac{1}{e^{\ln(x)}} = \frac{1}{x} = x^{-1} \] Amazing! This derivative is the "missing power" -- we didn't know how to get this particular derivative using the power rule: it would have come from the power $x^0$ -- but that's a constant, so its derivative is 0. This creates a mysterious connection between power functions and the exponential function, and its inverse, the log.
Notice that \(\frac{1}{x}\) is our friend the hyperbola. Notice also that this function is odd -- it should be the derivative of an even function. We can extend the $\ln(x)$ function to the left, by considering $\ln(|x|)$:
- By the way, this allows us to now clearly understand those derivatives of other exponential functions. Consider, for example, the function \[ g(x)=2^x \] Because we now have the inverse function of $e^x$, we can write \(2=e^{\ln(2)}\) -- more generally we need to remember that, as inverses, \(x=e^{\ln(x)}\) -- at least for positive values of \(x\). And, last I checked, 2 is positive: \[ g(x)=2^x=\left(e^{\ln(2)}\right)^x = e^{\ln(2)x} \] That might look a little scary, but $\ln(2)$ is just a number -- approximately 0.69. So we can now compute the derivative of $2^x$ easily, thinking of it as a composition -- and so using the chain rule: \[ g'(x)=\ln(2) e^{\ln(2)x}=\ln(2) 2^x = \ln(2) g(x) \] More generally, if $g(x)=b^x$, \[ g'(x)=\ln(b) e^{\ln(b)x}=\ln(b) b^x = \ln(b) g(x) \] And the choice of $b=e$ gives that amazing function that satisfies \[ g'(x)= \ln(e) g(x)= 1 \cdot g(x)= g(x) \]
- Our authors consider some additional tools that we can use based
on knowing the derivative of \(\ln(x)\). One of these is logarithmic
differentiation: let's illustrate it with an example from our text,
CheckPoint 3.54:
Use logarithmic differentiation to find the derivative of \(f(x)=x^x\).
This is quite an interesting function, especially as \(x \to 0\): what is \(0^0\)? That's a really interesting philosophical question!
Logarithmic differention works like this: take logs of both sides, simplify, and differentiate: \[ \ln(f(x)) = \ln(x^x) = x\ln(x) \] Therefore the chain rule on the left and the product rule on the right gives \[ \frac{f'(x)}{f(x)} = \ln(x) + x\frac{1}{x} = \ln(x) + 1 \] or \[ f'(x) = \ln(x) + x\frac{1}{x} = f(x)(\ln(x) + 1) = x^x(\ln(x) + 1) \] as seen in this image:
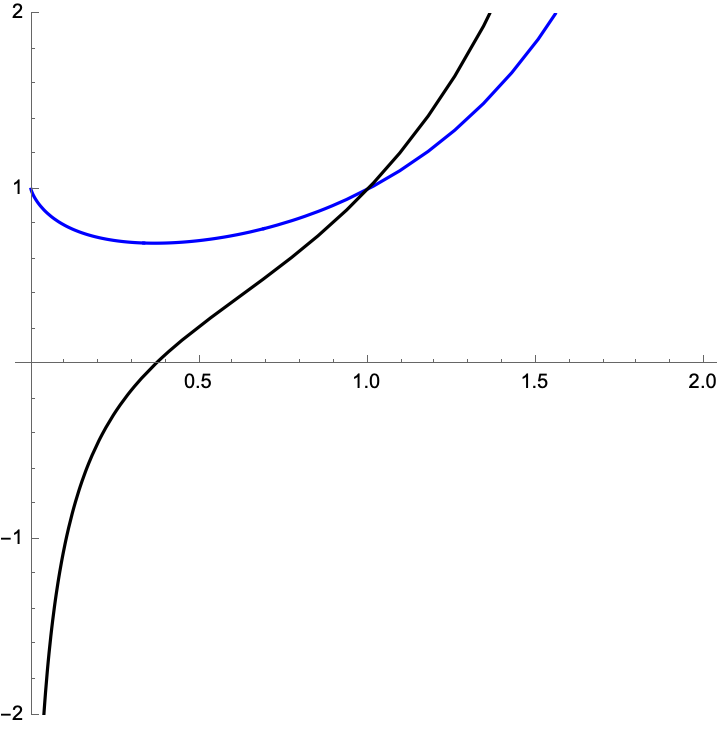
- Let's do some problems:
- Ex 336: transforming exponentials to base e
- Ex 354:
- 359: population of Toledo, OH.
The population of Toledo, Ohio, in 2000 was approximately 500,000. Assume the population is increasing at a rate of 5% per year.
- Write the exponential function that relates the total population as a function of \(t\).
- Use a. to determine the rate at which the population is increasing in \(t\) years.
- Use b. to determine the rate at which the population is increasing in 10 years.
- Then time for a quiz!
- We're going to proceed exactly as we did before, only this time
we're in luck: the function $f(x)=e^x$ is, in fact, invertible -- no
need to restrict a domain!
- The value of E (according to Wolfram Alpha)
- For a different take: Active Calculus, Section 2.6: Inverse functions and their derivatives
- Another Mathematica file, to review the shapes of basic functions, and some of their properties.
- Here's some Mathematica showing the Ceiling And Floor functions at work, to solve the Checkpoint 1.15 problem about postal rates.