- Your quiz is returned:
- This week we have our first exam. It will cover all the material
we've done since the start.
No new material or homework will be assigned prior to the exam, so you want to go back over whatever you might have missed. It's a good time to ask questions in class, too.
You may have a one-page (front and back) sheet for formulas, etc. on Thursday (recall that we have a techno-free test on Thursday, and then Mathematica test on Friday). You may use copies of your labs for Friday.
Today we'll wrap up what we were doing last week (trigonometric stuff), and then Tuesday we'll review.
- Before we do, however, I want to address a little mystery that
occurred during our lab, Lab
04. I suggested that something would happen when we tried
to compare Mathematica's solution to the correct one for
\[
\int \sec(x) d x
\]
(which we did by substitution, after multiplying by a particularly unusual form of one!); and then using the fact that \[ \int \frac{1}{x} d x = \ln(|x|)+C \]
Noting the importance of the absolute value, since \(\frac{1}{x}\) is an odd function, and should have an even anti-derivative.
I thought that this is what we would see:
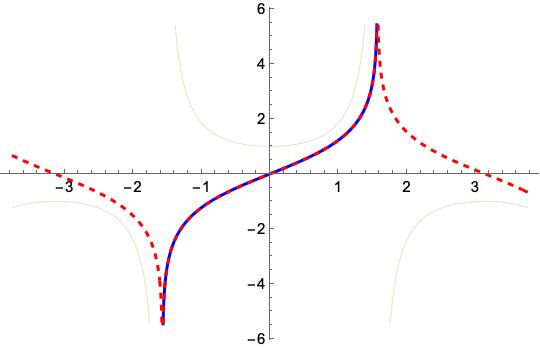
It's worse than I thought, however: using Mathematica's choice for the anti-derivative of the secant function, \(\coth ^{-1}(\sin (x))\), leads to this, for example:
\(\int_{-0.1}^{0.3} \sec(x) d x = 0.4047711 -3.141593 i = \) \(ArcCoth[Sin[0.3]]-ArcCoth[Sin[-0.1]]\)
This is why no graph appeared when I tried to graph it on Friday: the solution was complex. Ironically I use an older version of Mathematica at home, and it worked differently there -- wrong, but differently!:) Their new improved version of Mathematica has a different kind of bug.
It's a bug, but perhaps also a feature sometime (if you're doing complex analysis, say, which generalizes univariate calculus).
My point is made however: that being that one should take all technology with a grain of salt, and realize that your brain and mathematical reasoning is in important part of the equation!
- One particularly useful set of functions that we encounter in
this section is the hyperbolic trig functions, which are defined
as follows:
\[
\sinh(x) \equiv \frac{e^x-e^{-x}}{2}
\]
\[
\cosh(x) \equiv \frac{e^x+e^{-x}}{2}
\]
\[
\tanh(x) \equiv \frac{\sinh(x)}{\cosh(x)}
\]
These functions behave in ways similar to the regular trig functions,
in spite of being based off of exponential functions. In particular,
- \(\sinh(x)\) is odd
- \(\cosh(x)\) is even.
- \(\sinh'(x) = \cosh(x)\)
- \(\cosh'(x)=\sinh(x)\)
And there are other familiar-looking identities (but with some slight changes in the symmetries, as you may have noticed above in the derivative for cosh):
\[ \begin{align} 1 &= \cosh^2(x)-\sinh^2(x) \\ \sinh(x + y) &= \sinh x \cosh y + \cosh x \sinh y \\ \cosh(x + y) &= \cosh x \cosh y + \sinh x \sinh y \\ \end{align} \]
- We used these functions to handle the second of these two cases we
considered below, and it was entirely analogous to the
first case (which was handled by tranditional trig
function substitutions).
- $\displaystyle
\int^{}_{} \sqrt{a^2-x^2}\ d x$
- $\displaystyle \int^{}_{} \sqrt{1+x^2}\ d x$ (in this case, we'll make use of those hyperbolic trig functions to solve it).
Let's now do that second integral using a different substitution: \(x=\tan(\theta)\).
This will give us a chance to practice our trig substitution and integration by parts, as well!:)
- $\displaystyle
\int^{}_{} \sqrt{a^2-x^2}\ d x$
- Let's check out our worksheet for this unit.
In particular, we'll begin by examining how to handle the triangle in that example.
- Mathematica on-line is an option, if you are at a computer without Mathematica installed. I've tried it and it worked pretty well!