- Reminder: stow those cellular rectangles.
- You have a homework due today -- section 14.1.
- 14.2 problems are now assigned, and due next Tuesday.
- Please read 14.3 for Thursday.
- If you're not familiar with Mathematica, you may want to try my Getting Started file.
- Let's go back to the univariate case (found in section 1.7 of your
book, p. 73):
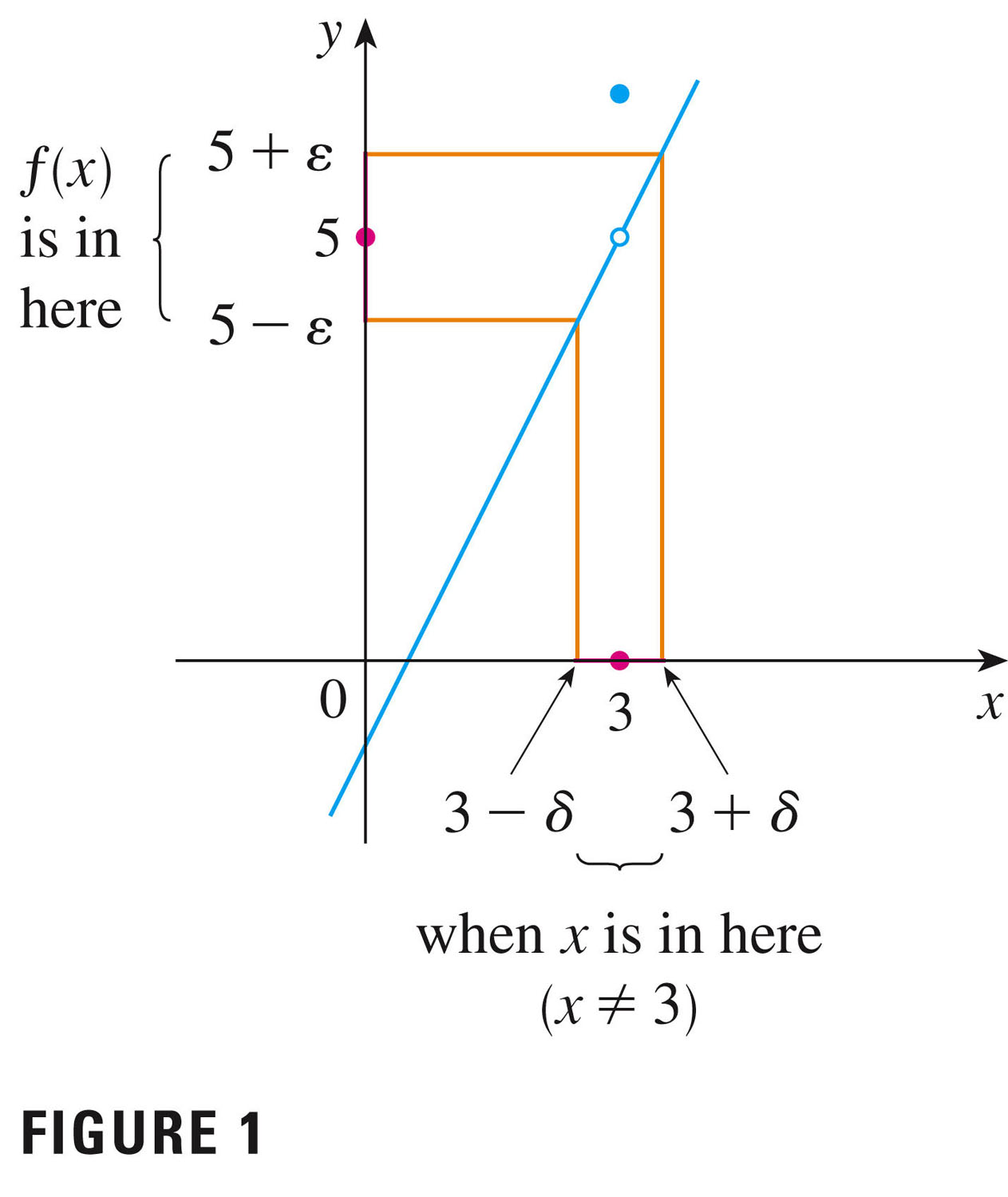
In this case it appears that there's a hole in the graph of the function (actually, a jump!) as domain values approach 3.
- We then ask "how should we modify this, generalize this, for multivariate functions?"
- In the univariate case, how can a limit fail to exist? Let's
consider the limit as $x \to 0$ in several different situations:
- Single holes are no problem;
- Holes with jumps are no worse:
- Cliffs are bad (including infinite ones);
- Functions may fail to "settle down": $\sin\left(\frac{1}{x}\right)$ around
x=0:
- Single holes are no problem;
- The same sorts of problems will occur for multivariate functions. But,
ironically, limits may exist along particular lines of approach but not
agree. This is something new and different. Let's take a look at p. 917, Tables
1 and 2.
Example 2, p. 919 is also interesting.
- The generalization of the univariate limit of section 1.7 is on p. 917,
and well illustrated on p. 918:
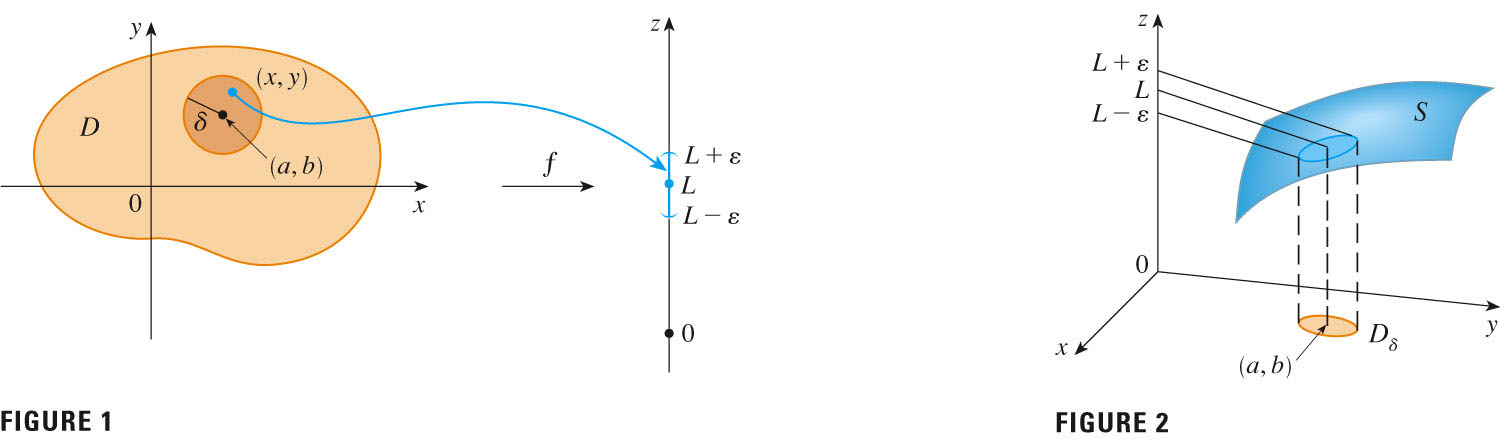
- The difference is in the domain, as usual. Instead of a
segment surrounding a, we require a circle surrounding
(a,b); in general, a ball surrounding the point in the
domain at which we desire the limit, if it exists.
Question: in the definition we find this expression:$0 < {\sqrt{(x-a)^2+(y-b)^2}} < \delta$ - What kind of animal is that? What's the geometric meaning?
- How does it generalize the 1-d case?
- Issued a challenge about getting within a tiny value
(epsilon) of the limiting value L, we must be able to find a ball small enough (as indicated by radius
) that function values within that "delta-neighborhood" are within
of L.
- The difference is in the domain, as usual. Instead of a
segment surrounding a, we require a circle surrounding
(a,b); in general, a ball surrounding the point in the
domain at which we desire the limit, if it exists.
- The next step is to generalize continuity. That's pretty easy:
A function $f$ of $x$ is called ${\bf{continuous}}$ at $(a,b)$ if
\[
\lim_{(x,y) \to (a,b)} f(x,y) = f(a,b)
\]
We say $f$ is ${\bf{continuous}}$ on $D$ if $f$ is continuous at every point
$(a,b)$ in $D$.
The good news is that the multivariate versions of the standard functions extend their continuity properties into multivariate forms: in particular, polynomials, rational functions, power functions, exponential functions, and trig functions are continuous on their domains.
Furthermore, compositions of continuous functions are continuous as in the univariate world. So there are some nice results that extend up from univariate calculus.
Note: it's important to recall the difference between continuous (connected) and smooth (differentiable) functions:
A function may be continuous (connected) but not differentiable; but if it's differentiable (smooth), it's continuous.
Continuous, but not smooth Smooth, hence continuous Continuity does not imply differentiability. Differentiability implies continuity. - Now let's take a look at some problems, involving limits and Problems involving continuity:
again, invoke theorems wherever you can.
-
- Examples 1-3 illustrate ways in which functions fail to
have a limit at a point.
We've already looked at #2, so let's see what examples 1 and 3 have to tell us.
- p. 923, #4:
1.0000 0.8824 0.3846 -0.3846 -0.8824 -1.0000 0.8824 1.0000 0.6000 -0.6000 -1.0000 -0.8824 0.3846 0.6000 1.0000 -1.0000 -0.6000 -0.3846 -0.3846 -0.6000 -1.0000 1.0000 0.6000 0.3846 -0.8824 -1.0000 -0.6000 0.6000 1.0000 0.8824 -1.0000 -0.8824 -0.3846 0.3846 0.8824 1.0000 - #6 -- use theorems to solve this one.
- #9
- #14 -- uses a trick, and theorems.
- Let's take a peek at Example 4, and see it working in #16. These arguments
are a little tricky!
We can do #16 by the definition, or by using limit laws from univariate calculus (think of the function as a product).
- #30, p. 924
- #32
- #38
- Examples 1-3 illustrate ways in which functions fail to
have a limit at a point.
- Links:
-
Website maintained by Andy Long. Comments appreciated.