Day 5 in Mat329

Last time

Next time

Today:

Announcements
- Your 14.1 homework is returned. My random choices were 1, 12, and 46.
  Please:
  - Do your homework!
  - show your work
  - label your graphs
- 14.2 problems are due next Tuesday.
- Tomorrow we'll have our first quiz at the end of the hour. We'll work on Mathematica again, so please bring your laptops and get Mathematica installed (if you haven't already).
Today we wrap up section 14.2: Limits and Continuity, and then start section 14.3: Derivatives
- Let's go back to the univariate case (found in section 1.7 of your book, p. 73):
  
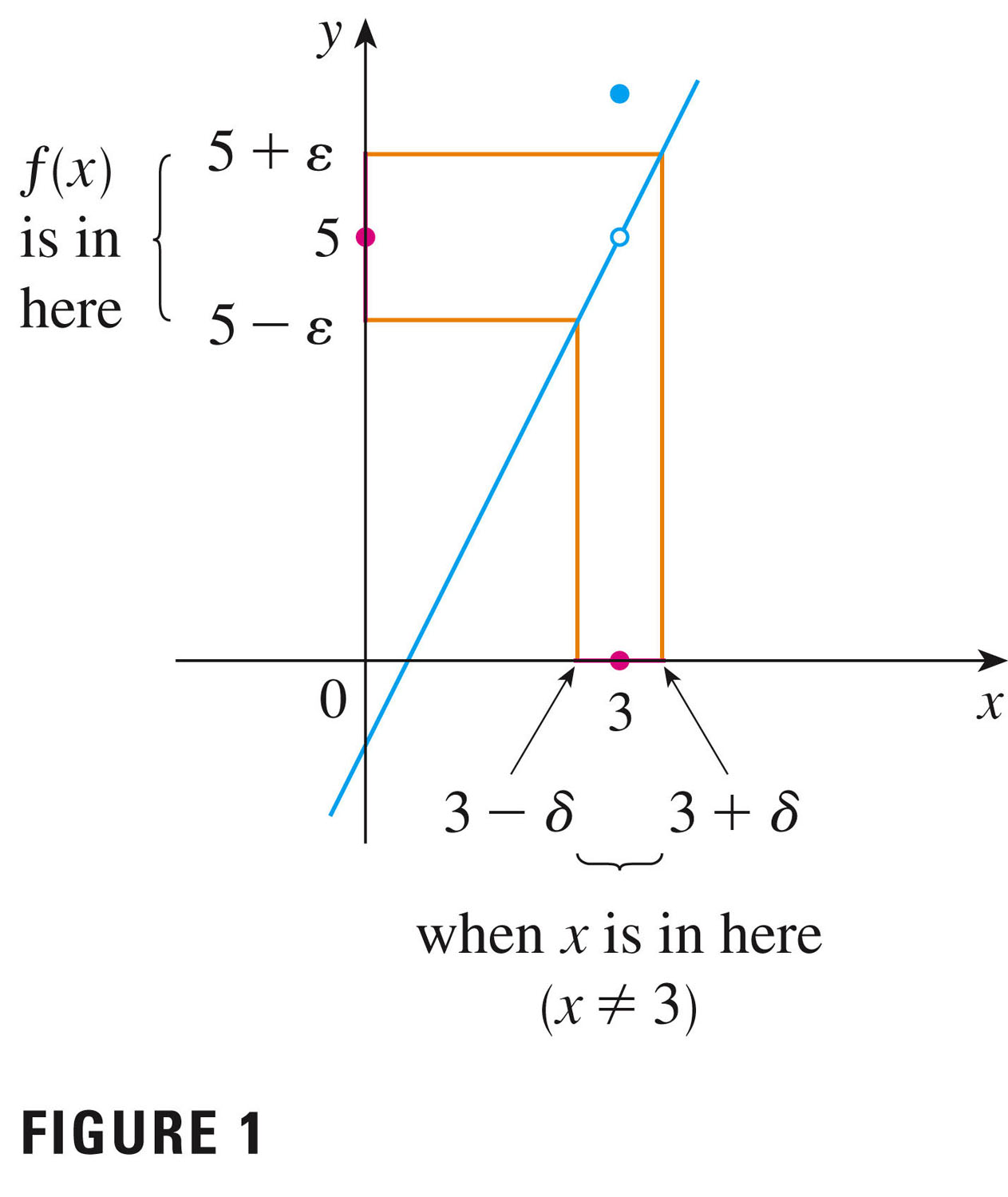
  In this case it appears that there's a hole in the graph of the function (actually, a jump!) as domain values approach 3.
- We then ask "how should we modify this, generalize this, for multivariate functions?"
- In the univariate case, how can a limit fail to exist? Let's consider the limit as $x \to 0$ in several different situations:
  - Single holes are no problem;
  - Holes with jumps are no worse:
  - Cliffs are bad (including infinite ones);
  - Functions may fail to "settle down": $\sin\left(\frac{1}{x}\right)$ around x=0:
- The same sorts of problems will occur for multivariate functions. But, ironically, limits may exist along particular lines of approach but not agree. This is something new and different. Let's take a look at p. 917, Tables 1 and 2.
  Example 2, p. 919 is also interesting.
- The generalization of the univariate limit of section 1.7 is on p. 917, and well illustrated on p. 918:
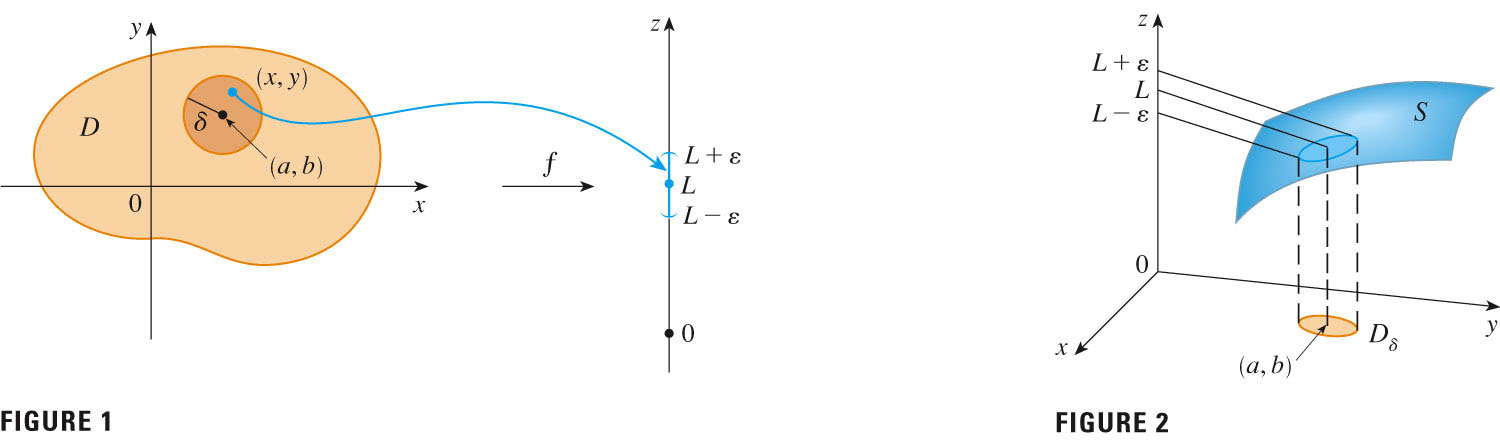
  - The difference is in the domain, as usual. Instead of a segment surrounding a, we require a circle surrounding (a,b); in general, a ball surrounding the point in the domain at which we desire the limit, if it exists.
    
    Question: in the definition we find this expression:
    
    $0 < {\sqrt{(x-a)^2+(y-b)^2}} < \delta$
    - What kind of animal is that? What's the geometric meaning?
    - How does it generalize the 1-d case?
  - Issued a challenge about getting within a tiny value $\epsilon$ (epsilon) of the limiting value L, we must be able to find a ball small enough (as indicated by radius $\delta$ ) that function values within that "delta-neighborhood" are within $\epsilon$ of L.
- The next step is to generalize continuity. That's pretty easy: A function $f$ of $x$ is called ${\bf{continuous}}$ at $(a,b)$ if \[ \lim_{(x,y) \to (a,b)} f(x,y) = f(a,b) \] We say $f$ is ${\bf{continuous}}$ on $D$ if $f$ is continuous at every point $(a,b)$ in $D$.
  The good news is that the multivariate versions of the standard functions extend their continuity properties into multivariate forms: in particular, polynomials, rational functions, power functions, exponential functions, and trig functions are continuous on their domains.
  Furthermore, compositions of continuous functions are continuous as in the univariate world. So there are some nice results that extend up from univariate calculus.
  Note: it's important to recall the difference between continuous (connected) and smooth (differentiable) functions:
  A function may be continuous (connected) but not differentiable; but if it's differentiable (smooth), it's continuous.
  
  Continuous, but not smooth Smooth, hence continuous
  
  Continuity does not imply differentiability. Differentiability implies continuity.
- Now let's take a look at some problems, involving limits and Problems involving continuity: again, invoke theorems wherever you can.
  1. Examples 1-3 illustrate ways in which functions fail to have a limit at a point.
    We've already looked at #2, so let's see what examples 1 and 3 have to tell us.
  2. #4, p. 923
  3. #6 -- use theorems to solve this one.
  4. #9
  5. #14 -- uses a trick, and theorems.
  6. Let's take a peek at Example 4, and see it working in #16. These arguments are a little tricky!
    We can do #16 by the definition, or by using limit laws from univariate calculus (think of the function as a product).
  7. #30, p. 924
  8. #32
  9. #38
Today we start section 14.3, on partial derivatives.
Here is "the most important definition in calculus" -- the limit definition of the derivative function, $f'(x)$: \[ f'(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h} \]
This is what we want to generalize.
- Take a look at Table 1, p. 925. How can we use the univariate idea?
- What about other directions? Think about a topo map -- you can set off in any direction from a point (often): what does the partial derivative mean in any direction?
- #2, p. 935
So here's the partial with respect to $x$: \[ f_x(x,y) = \lim_{h \to 0}\frac{f(x+h,y)-f(x,y)}{h} \]
We think of $y$ as fixed in this derivative. It's not varying. Only $x$ is varying; is variable.
And here's the partial with respect to $y$: \[ f_y(x,y) = \lim_{h \to 0}\frac{f(x,y+h)-f(x,y)}{h} \]
They're easy to compute, actually: e.g., for $f_x$, just imagine that $y$ is a parameter, and differentiate in the univariate way with respect to $x$.
Figures 4 and 5 on p. 928 give us this idea very nicely.
Problems:
1. #5, p. 936
2. #10
3. #15
4. #24
Higher partial derivatives are easy to calculate, as well, since each partial is again a multivariate function in its own right. So do it again!
We think of second derivatives in the univariate world as saying something about curvature, and the same is true in the bivariate case.
- #53, p. 937 (note the notation, p. 930)
The world is governed by partial differential equations, such as the heat equation, the wave equation, Laplace's equation, etc.
- #75, p. 937
There is an important theorem in this section: Clairaut's theorem: Suppose $f$ is defined on a disk $D$ that contains the point $(a,b)$. If the functions $\frac{\partial^2 f}{\partial x \partial y}$ and $\frac{\partial^2 f}{\partial y \partial x}$ are both continuous on $D$, then \[ \frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x} \]
- #74, p. 937 (Clairaut's theorem tells us that we don't need to consider $f_{yx}$).

Website maintained by Andy Long. Comments appreciated.