- Your 15.8 and 15.9 homework is due Tuesday, next week.
- Lunch!

- Your 15.7 homework is returned: graded 10, 24, 44
- #10: give numerical approximation
- #24: don't forget Mathematica check (part b)
- #44: I love it when you say "by symmetry...". Note: $kabc=M$.
- We'll be starting 16.1 tomorrow (I hope). I may do a little Mathematica triple integral practice with you, however.
The volume element ($dV$) is given by $rdrd{\theta}dz$, as one can see in Figure 7, p. 1054:
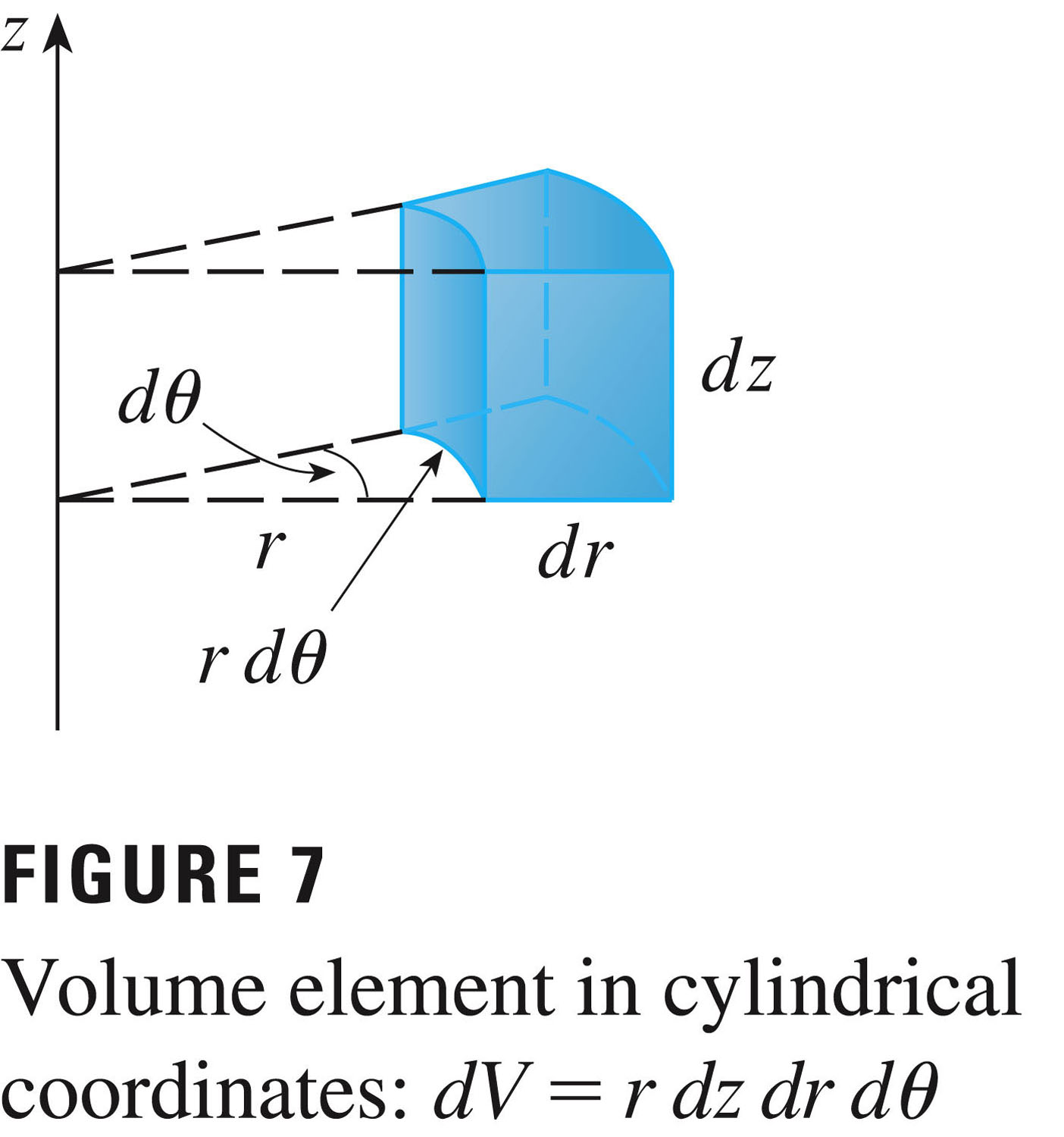
This is a simple generalization of the polar formula of the area element $dA$.
- #1, p. 1055
- #3
- #13
- let's revisit the problem, #20, p. 1049.
- #26
- Then we'll try #31 -- Mt. Fuji!
In every event, you need to think about how best to represent the situation that you're dealing with, and symmetry and structure may indicate that a particular coordinate system is particularly sensible.
Problems always start out the same, e.g. $W=\int\!\int\!\int\!dW$ -- then our job is to figure out how best to rig things so that the limits of integration, and the differential $dW$ make doing the integral as easy as possible.
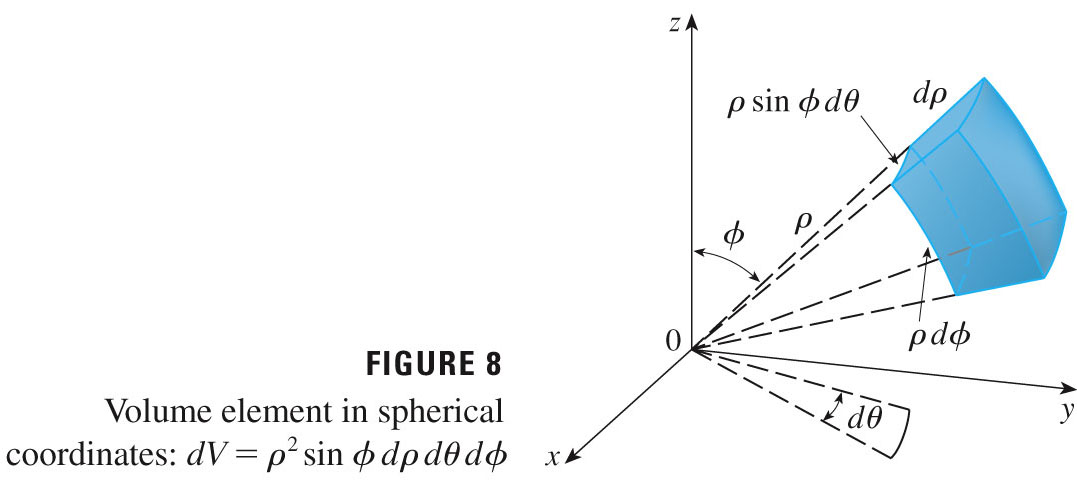
We'll just look at some problems that have spherical symmetry that we might exploit. Figures 5 and 8 are worth examining in some detail....
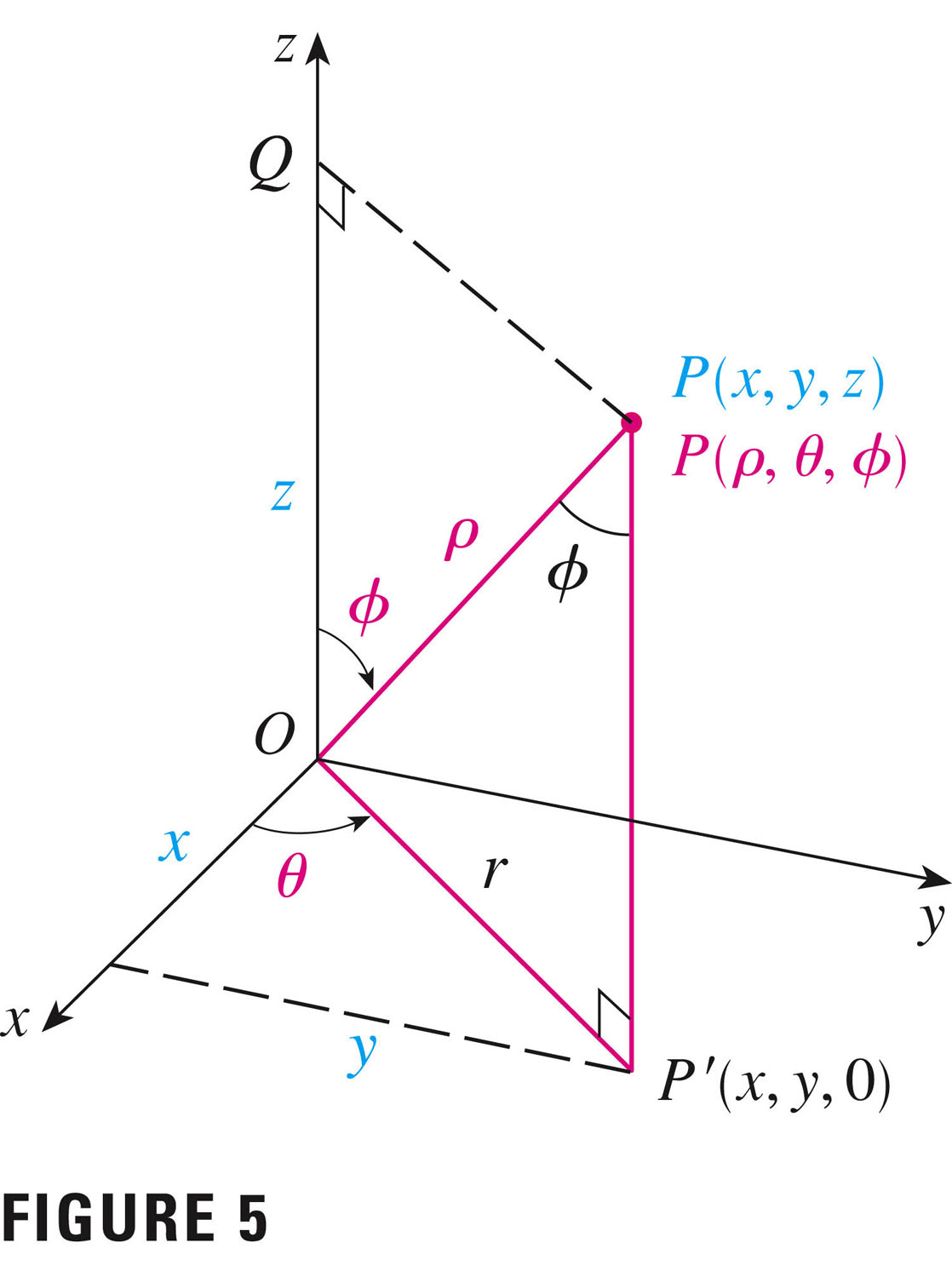
\[ x=\rho\sin{\phi}\cos{\theta} \hspace{1in} y=\rho\sin{\phi}\sin{\theta} \hspace{1in} z=\rho\cos{\phi} \] and the volume element becomes \[ dV = \rho^2\ \sin(\phi)\ d\rho\ d\theta\ d\phi \]
- #1a
- #3b
- #8
- #19 and 20
- #21
- #38