Day 36 in Mat329

• Your 15.8 and 15.9 homework is due Tuesday, next week.
• Lunch! I hope that you're hungry....
  

We now consider vector-valued functions in multivariate space. We've seen these before, however: if we have a multivariate function $f$ which is differentiable, then it has a gradient at every point, pointing to higher values of $f$.

This is an important example: a gradient field.

• Not all vector fields are gradient fields, however: in general, we might think of a vector field F as ${\bf{F}}=\langle P(x,y),Q(x,y) \rangle$.

  Q: Is the vector field of Example 1 a gradient field?

  If F is a gradient field, then it is called a conservative vector field (and $f$ its potential function).

• Examples:
  • Jared Antrobus (former NKU student and now PhD student in mathematics at UK) provided some Mathematica code that gives insight into the gradient field, and its relationship to maxes and mins: Classify3DGradientField.nb

    This code plots the functions, with maxes and mins, but adds in the contour lines, and also the gradient lines.

    Let's use this to take a look at Example 6, p. 1084.

    

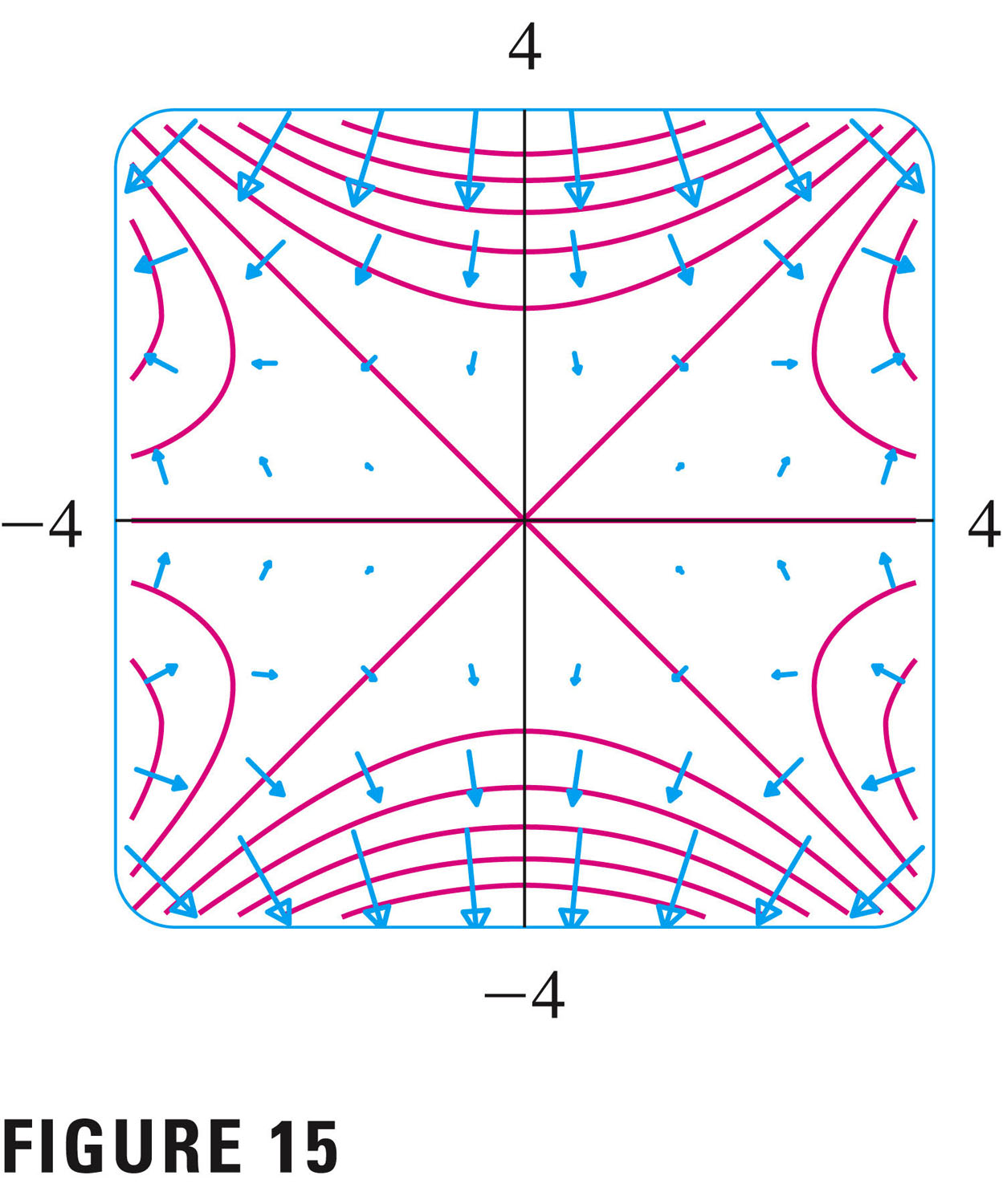
  • #11-14, 1085
  • #1
  • #2
  • #21
  • #25
  • #34
  • #35 -- I've been plotting streamlines, so let's talk about them!:)