- You have a new homework for
section 4.4. Let's make it due on Wednesday of next week.
This will be your last "homework" to turn in; any other assignments will be part of your final takehome (thinking of 6.2, 6.3).
- Your take home exams are returned (30% of your grade).
- Keys:
- Octave implementations.
- Keys:
- Your in-class exams are also returned (70% of your grade).
- Your key
- Mathematica "key" (for #1 and #2) (pdf)
- You may resubmit your test, with corrections (done separately -- don't mark your first copy) by Monday, for 1/3 of missed points back.
- I'd like Danny to go over #4, if he's willing....
- Your sigmacs are due on Friday. How are those coming?
- Monday was a work day, and I hope that you made some progress
toward deciding on a project as well.
I've talked to two of you, who seem to have a pretty solid project idea; who still needs one?
- Second derivative and higher formulas require a bit more work: we
need to use Taylor series to derive these methods, and their error
terms (you got more practice with that on the take home, of course!).
- Integral formulas can be obtained in similar fashion, and
our author spotlights Gaussian elimination as a
technique to get extraordinary precision (the scheme
gets high degree polynomials exactly right). The
placement of the nodes is at the roots of special
polynomials, called Legendre polynomials.
While there is no motivation for this, the author shows that it works. Maybe it's just magic.... or a good project?
- We now have some integration formula, like
- trapezoidal
- midpoint
- simpson's rule
In fact, Simpson's rule is just a weighted average of the two previous methods (remember Long's rule: whenever you have two approximations, you have a third -- an average).
In particular, the midpoint method is twice as good as the trapezoidal method, and the errors tend to be of opposite sign. This analysis is based off of an approximating parabola
So your code for the Simpson's rule is \[ simp(f,a,b) = \frac{1}{3}\left(2*mid(f,a,b)+trap(f,a,b)\right) \]
- The first two methods (trapezoidal and midpoint) can be considered
integrals of linear functions.
The trapezoidal method is the integral of a linear interpolator of two endpoints, and midpoint is the integral of the constant function passing through -- well, the midpoint of the interval!
This illustrates one important different application of these two methods:
- trapezoidal requires the endpoints;
- midpoint doesn't require the endpoints.
These methods are both examples of what are called "Newton-Cotes methods" -- trapezoidal is a "closed" method, and midpoint is "open".
-
We can turn them into powerful tools for doing serious integration, but
in order to do so we have to consider some improvements.
The first idea is to paste these methods together on a "partition" of the interval of integration -- that is, multiple sub-intervals, on each one of which we apply the simple rule. This pasted up version is called a "composite" rule.
We start by assuming a partition of the interval $[a{,}b]$ that is equally spaced. But in the end, we should let the behavior of $f$ help us to determine the the partition of the interval. This is called "adaptive" integration.These figures illustrate one of the methods in action -- which one?
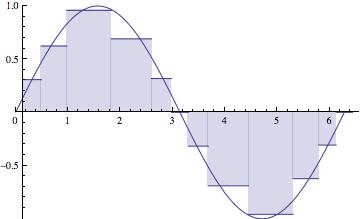
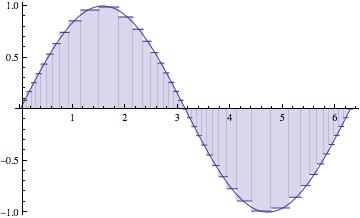
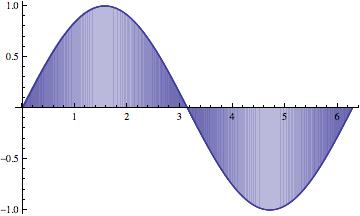
The maximum subinterval width ($||{P}||$) goes to zero. The partition gets thinner and thinner, as the number of subintervals (n) goes to $\infty$.
The approximations get better and better, of course, as $n \longrightarrow \infty$.Notice that the larger subintervals occur where the function isn't changing as rapidly.
This scheme would be called "adaptive", adapting itself to the function being integrated. That's what we're going to shoot for. - The derivation of the trapezoidal method is carried out in this
section (p. 169). The author wants to consider
\[
\int_{x_0}^{x_0+h}f(x)dx \approx \frac{h}{2}(f(x_0)+f(x_0+h)),
\]
but more generally we consider
\[
\int_{a}^{b}f(x)dx \approx \frac{b-a}{2}(f(a)+f(b)),
\]
where $h=(b-a)/2$ (note that this is then different from our author's
\(h\)).
Let's have a look at the derivation of the composite rule on page 168, and, in particular, note the error term (defined as the exact integral minus the approximation), which can be written as \[ -\frac{b-a}{12}h^2f^{(2)}(\xi), \] with $\xi \in (a,b)$ and with (our author switches focus to \(n\), in part, I fear, because of his infatuation with stencils....:)
(Look at the dance he does in the pseudo-code: what purpose does his \(h\) serve?)
- Then on page 171, our author describes the process whereby we can
make the scheme adaptive (project opportunity: the same process
can be used to create an adaptive plotting routine!). Let's have a look
at that.
This is a "divide and conquer" algorithm. Very slick!
Here's some Mathematica code that I wrote to illustrate the idea. It includes examples of how we can turn this into a plotting routine....
- Let's get started on one of your homework problems, #27, p. 173.
- Our Textbook: Tea Time Numerical Analysis (Leon Q. Brin)
- A paper my dad and I wrote about integration techniques: including lots of details!:)
- Some notes
- An interesting
alternative derivation technique. Here, for example, is a
four-point forward difference formula for the derivative, obtained
using the Newton polynomial interpolator (notice, however, that the \(x\)
values in the numerator should actually be \(y\) values -- function values):

But the idea is really swell, and I am delighted by this method!
- An example of cubic splines: how do we intepolate two
points and their slopes using a cubic? We can derive the so-called
"Hermite spline" as a variant of Lagrange interpolation, featuring "get
out of the way" functions!
Here's another picture of how we might build one of these.
- Homework solutions:
- 1.1 (Mathematica)
- 1.2 (Mathematica)
- 1.3 (Mathematica)
- 2.1 (Mathematica)
- 2.2 (Mathematica)
- 2.3 (Mathematica)
- 2.4 (Mathematica)
- 3.2 (Mathematica)
- 3.3 (Mathematica)
- 4.1 (Mathematica)
- My Mathematica code for Section 2.6. Muller code, too.
- My Octave Project for 2.6 homework.
- Octave project for 2.5
- Divided Differences. I use these in my Muller code, and they will prove useful when it comes to interpolating polynomials.
- Author's octave code for these complex fractal convergence diagrams
- Newton's method in Mathematica
- fixed point with Aitken's acceleration in Mathematica
- Some nice notes (and code) snippets on fixed point iteration, including these acceleration techniques.
- fixed point in Mathematica
- Check out how my bisection works, and how it is applied to arcsine....
- Various sins....