Some thoughts for the course:
-
There are three kinds of lies: lies, damned lies, and statistics
-

- Name (that you want me to call you)
- Hometown
- What is your calling? ("a calling has to do with one's larger purpose, personhood, deepest values, and the gift one wishes to give the world.... A calling is about the use one makes of a career." David Orr, Earth in Mind)
- What is your dream job?
- What is something special about you?
- What is your height? (If you don't know it, we can figure it out!)
- Syllabus
- Tentative Schedule
- An important resource: the Math/Stat lab (MEP 457)
The Math & Stat Lab will open this semester on Tuesday, January 17 at 9am. The lab will be open M-R from 9-3, and F 9-12.
- Class agreement
- You'll need to print out the packets. These are found off the
homepage, linked to packets. Just
print them off as needed (because we may be making changes
along the way).
For next time, print off Packet01-NormalDistributions.pdf and bring it to class. We'll be filling it out as we go along on Wednesday.
- What do we mean by "Statistics"? What is/are Statistics?
- Statistics are numbers ("descriptive statistics")
First Definition of Statistics: Statistics are numbers calculated from a collection of data
"Data": items of information, either numerical or non-numerical (quantitative versus qualitative)
Examples of statistics:
- baseball "averages"
- percent, proportion of NKU students that graduated from the same high school as one of their parents
- average height of NKU students
- percentages of students preferring each type of soft drinks offered on NKU campus
- Statistics is a science ("inferential statistics")
Second Definition of Statistics: Statistics is a science that deals with the collection and summary of information that is then used to make interpretations, decisions, estimates, predictions, etc.
Examples:
- Polio Vaccine trials
- Calling elections before some voters have even voted (and
certainly before most votes have been counted)
- What makes this easy?
- Why did the 2000 Presidential Election take so long to call?
- A more mundane example: Heights of NKU students
- Let's try some inferential statistics. Inferential Statistics
is tied up with probability. We may hear someone make a statement,
and then we say "Nonsense!", or "That seems reasonable...."
But we may want to do more: we may want to test an assertion, to see what we can detect or infer from our examination of the data.
Example: So let's think about those NKU student heights:
- What's the probability that the class average height is above 7 feet?
- What's the probability that the class average height is below 7 feet?
- As we shift the "7 feet" part around, how will these probabilities change? In particular, begin dropping the 7 towards 4, and what would you see happening to the probabilities?
- A handout: in class, you'll
generally be bringing your own handouts! Please remember to print them
off in advance....
- Now let's figure out how we'd test some assertions:
- Suppose I assert that everyone in class is 6 feet tall.
- What could we do to test this assertion?
- In particular, why don't we need to know the height of everyone in class?
- Suppose I assert that the mean (or average) height is 6
feet.
- What could we do to test this assertion (without simply calculating the mean for the class! We're trying to be clever....)?
- By being clever are we being overconfident?
- How can we mix in notions of probability?
- Suppose I assert that everyone in class is 6 feet tall.
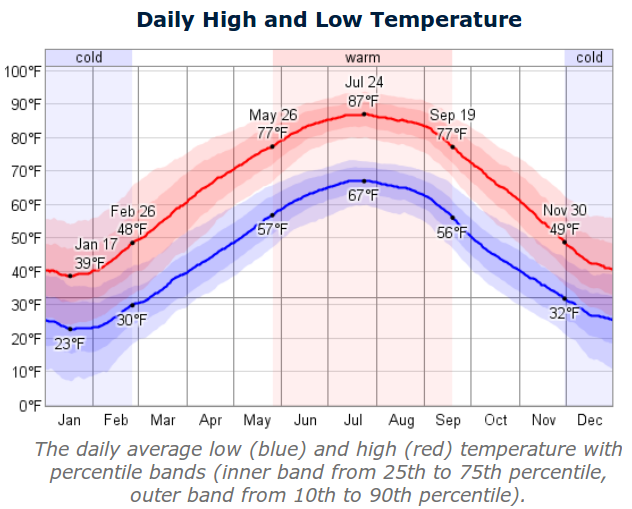
- What statistics are being shown in this graphic?
- How do we relate the statistics to probabilities?
- The high is forecast to be 61 degrees F on Thursday. How do you relate that to probabilities for this particular date?
- On Saturday, the high is forecast to be 39 degrees F. How do you relate that to probabilities for this particular date?
- Statistics are numbers ("descriptive statistics")
- How and why do the experts do statistics? (The Gallup (polling) Organization)
- and why do they always seem so unconfident?;)