Arborloos are toilets that make trees: Arborloos toilets (as we made them) require the use of three special shapes:
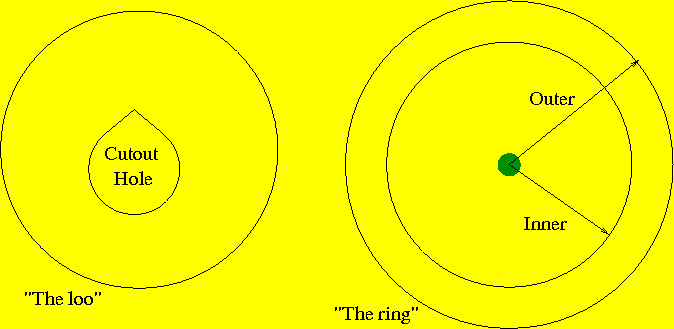
- a circle,
- a ring (a circle with a circle cut out of its center), and
- a "cutout" for the pooper hole.
This is how arborloo construction works:
- Choose the exact spot (point) where you want to plant the tree. [It's all about the tree!] Level the ground around that point.
- Draw two circles in the dirt, centered on the spot where you want the tree: the radius of one circle is the inner radius of the ring, and the radius of the other circle is the outer radius of the ring. The loo itself is of diameter one meter, and the inner and outer diameters of the ring are the same number of inches (x) from one meter: that is, Di=1-x and Do=1+x.
- Put pins in the ground (we used pieces of thin iron or small sticks) all around the circle.
- Interweave some thin fiber board material through the sets of pins (or anything that will serve as a dam, to keep the cement in or out, as the case may be).
- You're ready to pour the cement into the mold for the ring.
- Nearby, you find another nice level spot for the loo.
- Make a circle the radius of the loo. Repeat the steps to make a mold. We made a tool (a "dam") that we placed in the middle of the mold. It was made of wood and fiber board. When the cement was poured, the dam kept the cement out of the center, leaving a hole for the poop. After an hour, while the cement is still moist, the dam is removed, leaving the hole.
- The result should look like this.
- After the ring and loo harden, a hole is dug inside the ring, about a meter deep. Mud is slathered on the ring (like this), and the loo is picked up and placed on top of the ring (the mud helps keep the flies out).
- Finally we throw some dry leaves in the hole, and put a tight cover on the hole (again, to keep out the flies). Now it's ready to use!
- You'll probably want a little privacy, however, so you should
build some sort of structure to create privacy (while making it light enough so
that it can be moved easily -- after all, the shallow hole will fill up soon,
and you'll need to move your loo!)
- Terry shows off a loo
- The whole family in a loo
- Here's
mine, which I made from a fallen palm tree, which was simply
disintegrating (and taking up some space in our coffee field). We removed
the tree, and freed up some land for coffee (and exposed some that had been
crushed by the falling tree); then we turned the tree into something useful.
This illustrates our guiding principle on campus: "Turning problems into solutions".
This principle is at the heart of recycling. Better yet to remember the three Rs, in order: Reduce, Reuse, Recycle.
- Now how do we use the arborloo? Each time you use it, you cover your "offering" with a little dirt, and repeat until the loo is filled. Then you remove the "outhouse", the loo, and the cover, and fill the hole with dirt. After a couple of months (to let the "stuff" settle) plant a tree!
- Here are some directions for use that a student of mine prepared for our school in Ranquitte, Haiti. They're in Creole, the language of Haiti, but I think that you'll "get the picture"!
Activities/Questions/For Discussion:
- Our mason uses a pair of nails and a string to make a circle in
the dirt -- do you know how? Try it (who doesn't like playing in the
dirt?): get two nails (or suitable replacements) and a string, and draw
some circles of different sizes.
- How nice are your circles?
- What problems do you discover?
- Can you suggest small improvements on the technique?
- Any big improvements? Especially if you have to draw the same circle over and over?
- We wanted to use a single sack of cement for both the ring and the
loo. That wouldn't pose any problem, of course: we'd just mix up the concrete
using the sack of cement, and divide it into two piles: one for the loo, and
the other for the ring. We wanted to use half the concrete for the loo, and
half for the ring. We chose a loo of radius one meter (large enough for a
person to comfortably use), and we required that the ring and loo be of equal
thickness (a thickness that we chose so that they're each strong enough to
resist breaking).
Problem: In the picture above, did we choose the radii of the ring (the two radiuses, inner and outer) so that the ring will have the same volume of concrete as the loo?
Hints:- The two objects have the same thickness: if they have equal volumes, what is the relationship between their areas?
- You might know formulas for the area of a circle or a ring. Even so, the dam in the center of the ring will give you problems.
Possible solution strategies- "Throwing darts" with rice! (probability)
- Print out the picture, and paste it to a piece of cardboard. Cut out each shape, and weigh them with a small scale (like a postage scale). Here you use the strategy of Hint 1 in reverse!
- The methods of Activity 2 can be used to solve other interesting
problems. Google Earth is an application that allows one to visualize
and investigate positions on planet Earth. It provides satallite images
of the Earth at different scales. Images are often so good that one can
see cars, people, trees, etc. For example, here's a photo of the CFI campus in
Ranquitte, Haiti. So if we're wondering the percentage tree
cover a particular area has, we could take a satellite photo of the
area from Google Earth, and drop rice onto it, or we could cut out the
trees from the picture and weigh the respective pieces.
However, the use of grid-lines in GoogleEarth suggests an alternative approach: Using only whole "squares" (the squares aren't perfectly square, but you get the idea), categorize the 10x13=130 squares as the closest of 0, 25, 50, 75, and 100 percent, then take the weighted average: the number of each type of square times its percentage, and add them up and divide by 130. This will give you the approximate tree cover for this block of Ranquitte. You can use this table for your calculations.
Is there anything special about my choice of "cut-offs" (0, 25, 50, 75, and 100)? NO! They're just convenient numbers, and we hope that you can distinguish between "quarters": one quarter covered, on half covered, three quarters covered, etc.
- Here's a different style
of arborloo, using wood rather than cement (and a wooden
"box toilet" in the bottom right corner of the photo). One
thing we should learn early in life is that there's never just
one way to do a thing: the trick is to find the best
way! In mathematics, that's called optimization --
finding the optimal solution.
How would you build a loo?
-
Archimedes was an astonishing ancient: living at approximately 270 BC,
Archimedes is famous as the man who nearly single-handedly fought off a Roman
Army during the seige of Syracuse. By his wisdom, by his clever mechanical
devices, he defended his city. The king prevailed upon him to save the city,
and he succeeded for quite a while. Eventually, Archimedes's devices were not
enough, and the Romans invaded the city. As Archimedes drew in the sand, Roman
soldiers stepped on his drawings. Unable to hold his tongue, he scolded them,
and one of the soldiers ran him through with his sword.
At least that's the story I was told when I was young. It's very romantic, isn't it? Which means that it's authenticity is almost certainly in doubt!
Even so, I have always believed that the author of the Biblical book of Ecclesiastes (traditionally thought to be Solomon) referred to Archimedes in the following verses (quoted from the King James Version of the Bible -- chapter 9, verses 14-15):
14 There was a little city, and few men within it; and there came a great king against it, and besieged it, and built great bulwarks against it: 15 Now there was found in it a poor wise man, and he by his wisdom delivered the city; yet no man remembered that same poor man.
We remember you, Archimedes! There is more about Archimedes in these units. He was far ahead of the people of his time, a sort of Leonardo de Vinci of the ancient world. - Slicing and dicing for area
So what does Archimedes have to do with our nursery?
- Slicing and dicing for volumes
- Cistern volumes
When we built a cistern for the nursery that went on campus, we wanted to assure that the cistern would hold 600 gallons of water. As cisterns go, that is relatively small.
- Gauss and the sum of the first 100 counting numbers
Here's another great story that I was told: When Carl Friedrich Gauss was just a little boy, smaller than his name, he was a precocious student -- which some teachers consider as "troublesome": he was just too smart for his own good! One day, the teacher, exasperated by the talented student, decided to give him some "make work": "Add the counting numbers up to 100, and come back when you have the answer." Gauss took a few steps back towards his seat, spun around, and walked back to his teacher's desk: "5050".
The teacher, who'd hoped that this might entertain Carl for awhile, thought that perhaps the boy was wrong -- so he tediously and methodically added the numbers, and discovered that the result was -- 5050! How did Carl do it? Perhaps he explained to his teacher that he'd simply added up pairs of number: 100+1, 99+2, 98+3, ..., 51+50. He now had a sum of 101*50, or 5050: we don't know how he did it!
But to the credit of his teacher, rather than beating the boy (which some teachers might have done, out of frustration), he said "We've got to get you some professional help." And Gauss was guided to even better teachers, who could take him further along the road to his glory. He was nicknamed "Prince of Mathematicians" by E. T. Bell, biographer of mathematicians, in his book "Men of Mathematics".
- squares versus hexagons
Many fields are laid out on a rectangular grid. That is, you start a row, and every so often (e.g. two meter) you plant a coffee tree. Then, when that row is done, you start another row which is two meters from the first, and plant another row. Turns out that this is not optimal -- you can get more plants planted in the same space if you'll take just advice from bees.
When bees make their honeycombs, they make the walls out of regular hexagons, as illustrated in this figure

or in this hexagonal paper. The diagonal of a regular hexagon is twice the length of a side, as one can see (because a hexagon is made up of size regular triangles).
However, the distance W between parallel sides (of length L) is $W=\sqrt{3}L$:
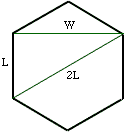
You can show this using the Pythagorean theorem: that for a right triangle, the sum of the squares of the side lengths is equal to the square of the hypotenus:
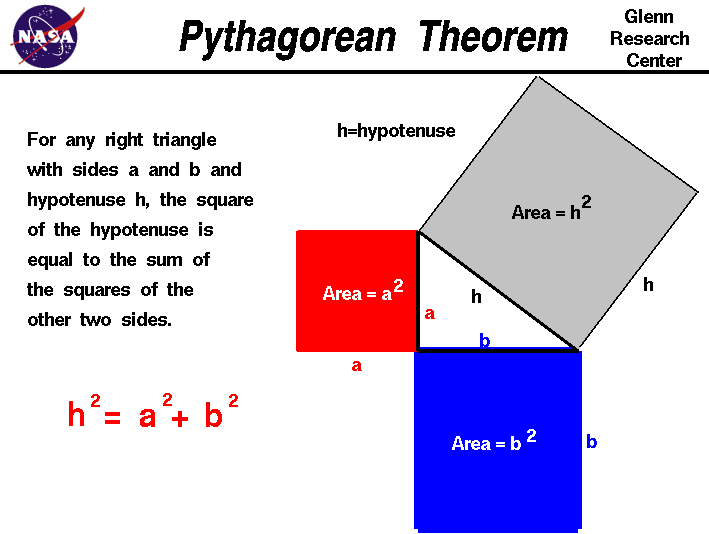
In our case the two side lengths are L and W, and the hypotenus is 2L, so we get \[ L^2+W^2=(2L)^2 \]
From this we can solve to find that $W^2=3L^2$, or $W=\sqrt{3}L$.
So in that sheet of hexagonal paper, I can imagine planting 230 plants (on the vertices -- corners -- of the hexagons), plus 103 at the centers, for a total of 333 plants.
- To do:
- Make a rectangular box around all the hexagons of the hexagonal paper, connecting all the vertices on the outside with a straight line. How big is this box? You can measure each side in terms of either L or W, or both. Can you show that the longer side is 11W, and the shorter side is 5W+4L?
The standard "rows" would be planted on a space of $(5W+4L)\times{11W}\approx{13L * {19L}}$.
Since we can get 14 plants on a space of 13L, and 20 plants on a space of 19L, we could get about 280 plants (280=14x20) on a regular grid.
The ratio $\frac{333}{280}\approx 1.19$ represents an increase of approximately 19% more plants.
- Note:
- If the ratio were 1, then we'd have the same number of plants in each case: the .19 part of the ratio represents the increase, or additional benefit, as a fraction. We need to multiply by 100 to get a percentage.
If we just plant in a hexagonal pattern we can get about 20% more food. That's a wonderful improvement in our use of the land.
The down side is that it's harder to move through the plants by machine. In a coffee field in Ranquitte, Haiti, this isn't a problem. It's probably not a problem in the raised beds of your garden at home, either....