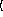 x
x
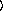
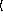 y
y
 [
[
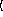 keyword arguments ...
keyword arguments ...
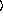 ])
])
(binomialreg-model
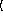 x
x
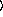
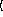 y
y
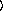
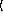 n
n
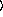 [
[
 keyword arguments ...
keyword arguments ...
 ])
])
(gammareg-model
 x
x
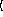 y
y
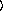
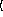 keyword arguments ...
keyword arguments ...
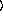 )
)
Three functions are available for constructing generalized linear
model objects. These functions are called as
(poissonreg-model
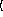 x
x
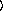
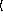 y
y
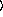 [
[
 keyword arguments ...
keyword arguments ...
 ])
])
(binomialreg-model
 x
x
 y
y
 n
n
 [
[
 keyword arguments ...
keyword arguments ...
 ])
])
(gammareg-model
 x
x
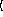 y
y
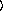
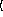 keyword arguments ...
keyword arguments ...
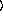 )
)
The
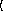 x
x
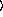 and
and
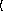 y
y
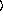 arguments are as for the
="2D regression-model=-1
function. The sample size parameter
arguments are as for the
="2D regression-model=-1
function. The sample size parameter
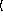 n
n
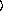 for binomial models can be either an integer or a sequence of integers
the same length as the response vector. All optional keyword
arguments accepted by the
="2D regression-model=-1
function are
accepted by these functions as well. Four additional keywords are
available:
="2D :link=-1
,
="2D :offset=-1
,
="2D :verbose=-1
, and
="2D :pweights=-1
.
The keyword
="2D :link=-1
can be used to specify an alternate link
structure. Available link structures include
for binomial models can be either an integer or a sequence of integers
the same length as the response vector. All optional keyword
arguments accepted by the
="2D regression-model=-1
function are
accepted by these functions as well. Four additional keywords are
available:
="2D :link=-1
,
="2D :offset=-1
,
="2D :verbose=-1
, and
="2D :pweights=-1
.
The keyword
="2D :link=-1
can be used to specify an alternate link
structure. Available link structures include
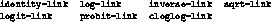
By default, each model uses its canonical link structure. The ="2D :offset=-1 keyword can be used to provide an offset value, and the keyword ="2D :verbose=-1 can be given the value ="2D nil=-1 to suppress printing of iteration information. A prior weight vector should be specified with the ="2D :pweights=-1 keyword rather than the ="2D :weights=-1 keyword.
As an example, we can examine a data set that records the number of months prior to an interview when individuals remember a stressful event (originally from Haberman, [ 2 , p. 2,]):
> (def months-before (iseq 1 18)) MONTHS-BEFORE > (def event-counts '(15 11 14 17 5 11 10 4 8 10 7 9 11 3 6 1 1 4)) EVENTS-RECALLEDThe data are multinomial, and we can fit a log-linear Poisson model to see if there is any time trend:
> (def m (poissonreg-model months-before event-counts)) Iteration 1: deviance = 26.3164 Iteration 2: deviance = 24.5804 Iteration 3: deviance = 24.5704 Iteration 4: deviance = 24.5704 Weighted Least Squares Estimates: Constant 2.80316 (0.148162) Variable 0 -0.0837691 (0.0167996) Scale taken as: 1 Deviance: 24.5704 Number of cases: 18 Degrees of freedom: 16
Residuals for the fit can be obtained using the ="2D :residuals=-1 message:
> (send m :residuals) (-0.0439191 -0.790305 ...)A residual plot can be obtained using
(send m :plot-residuals)The ="2D :fit-values=-1 message returns
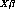 , the linear predictor
without any offset. The
="2D :fit-means=-1
message returns fitted mean
response values. Thus the expression
, the linear predictor
without any offset. The
="2D :fit-means=-1
message returns fitted mean
response values. Thus the expression
(let ((p (plot-points months-before event-counts))) (send p :add-lines months-before (send m :fit-means)))constructs a plot of raw counts and fitted means against time.
To illustrate fitting binomial models, we can use the leukemia survival data of Feigl and Zelen [ 4 , Section 2.8.3,] with the survival time converted to a one-year survival indicator:
> (def surv-1 (if-else (> times-pos 52) 1 0)) SURV-1 > surv-1 (1 1 1 1 0 1 1 0 0 1 1 0 0 0 0 0 1)The dependent variable is the base 10 logarithm of the white blood cell counts divided by 10,000:
> transformed-wbc-pos (-1.46968 -2.59027 -0.84397 -1.34707 -0.510826 0.0487902 0 0.530628 -0.616186 -0.356675 -0.0618754 1.16315 1.25276 2.30259 2.30259 1.64866 2.30259)A binomial model for these data can be constructed by
> (def lk (binomialreg-model transformed-wbc-pos surv-1 1)) Iteration 1: deviance = 18.2935 Iteration 2: deviance = 18.0789 Iteration 3: deviance = 18.0761 Iteration 4: deviance = 18.0761 Weighted Least Squares Estimates: Constant 0.372897 (0.590934) Variable 0 -0.985803 (0.508426) Scale taken as: 1 Deviance: 18.0761 Number of cases: 17 Degrees of freedom: 15This model uses the logit link, the canonical link for the binomial distribution. As an alternative, the expression
(binomialreg-model transformed-wbc-pos surv-1 1 :link probit-link)returns a model using a probit link.
The ="2D :cooks-distances=-1 message helps to highlight the last observation for possible further examination:
> (send lk :cooks-distances) (0.0142046 0.00403243 0.021907 0.0157153 0.149394 0.0359723 0.0346383 0.0450994 0.174799 0.0279114 0.0331333 0.0347883 0.033664 0.0170441 0.0170441 0.0280411 0.757332)This observation also stands out in the plot produced by
(send lk :plot-bayes-residuals)
Anthony Rossini