
Four functions are provided to help construct indicator vectors for categorical variables. As an illustration, a data set used by Bishop, Fienberg, and Holland examines the relationship between occupational classifications of fathers and sons. The classes are

The counts are given by
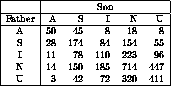
We can set up the occupation codes as
(def occupation '(a s i n u))and construct the son's and father's code vectors for entering the data row by row as
(def son (repeat occupation 5)) (def father (repeat occupation (repeat 5 5)))The counts can then be entered as
(def counts '(50 45 8 18 8
28 174 84 154 55
11 78 110 223 96
14 150 185 714 447
3 42 72 320 411))
To fit an additive log-linear model, we need to construct level indicators. This can be done using the function ="2D indicators=-1 :
> (indicators son) ((0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0) (0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0) (0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0) (0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1))The result is a list of indicator variables for the second through the fifth levels of the variable ="2D son=-1 . By default, the first level is dropped. To obtain indicators for all five levels, we can supply the ="2D :drop-first=-1 keyword with value ="2D nil=-1 :
> (indicators son :drop-first nil) ((1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0) (0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0) (0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0) (0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0) (0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1))
To produce a readable summary of the fit, we also need some labels:
> (level-names son :prefix 'son)
("SON(S)" "SON(I)" "SON(N)" "SON(U)")
By default, this function also drops the first level. This can again be
changed by supplying the
="2D :drop-first=-1
keyword argument as
="2D nil=-1
:
> (level-names son :prefix 'son :drop-first nil)
("SON(A)" "SON(S)" "SON(I)" "SON(N)" "SON(U)")
The value of the
="2D :prefix=-1
keyword can be any Lisp expression.
For example, instead of the symbol
="2D son=-1
we can use the string
="2D "Son"=-1
:
> (level-names son :prefix "Son")
("Son(S)" "Son(I)" "Son(N)" "Son(U)")
Using indicator variables and level labels, we can now fit an additive model as
> (def mob-add
(poissonreg-model
(append (indicators son) (indicators father)) counts
:predictor-names (append (level-names son :prefix 'son)
(level-names father :prefix 'father))))
Iteration 1: deviance = 1007.97
Iteration 2: deviance = 807.484
Iteration 3: deviance = 792.389
Iteration 4: deviance = 792.19
Iteration 5: deviance = 792.19
Weighted Least Squares Estimates:
Constant 1.36273 (0.130001)
SON(S) 1.52892 (0.10714)
SON(I) 1.46561 (0.107762)
SON(N) 2.60129 (0.100667)
SON(U) 2.26117 (0.102065)
FATHER(S) 1.34475 (0.0988541)
FATHER(I) 1.39016 (0.0983994)
FATHER(N) 2.46005 (0.0917289)
FATHER(U) 1.88307 (0.0945049)
Scale taken as: 1
Deviance: 792.19
Number of cases: 25
Degrees of freedom: 16
Examining the residuals using
(send mob-add :plot-residuals)shows that the first cell is an outlier -- the model does not fit this cell well.
To fit a saturated model to these data, we need the cross products of the indicator variables and also a corresponding set of labels. The indicators are produced with the ="2D cross-terms=-1 function
> (cross-terms (indicators son) (indicators father)) ((0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0) (0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0) ...)and the names with the ="2D cross-names=-1 function:
> (cross-names (level-names son :prefix 'son)
(level-names father :prefix 'father))
("SON(S).FATHER(S)" "SON(S).FATHER(I)" ...)
The saturated model can now be fit by
> (let ((s (indicators son))
(f (indicators father))
(sn (level-names son :prefix 'son))
(fn (level-names father :prefix 'father)))
(def mob-sat
(poissonreg-model (append s f (cross-terms s f)) counts
:predictor-names
(append sn fn (cross-names sn fn)))))
Iteration 1: deviance = 5.06262e-14
Iteration 2: deviance = 2.44249e-15
Weighted Least Squares Estimates:
Constant 3.91202 (0.141421)
SON(S) -0.105361 (0.20548)
SON(I) -1.83258 (0.380789)
SON(N) -1.02165 (0.274874)
SON(U) -1.83258 (0.380789)
FATHER(S) -0.579818 (0.236039)
FATHER(I) -1.51413 (0.33303)
FATHER(N) -1.27297 (0.302372)
FATHER(U) -2.81341 (0.594418)
SON(S).FATHER(S) 1.93221 (0.289281)
SON(S).FATHER(I) 2.06417 (0.382036)
SON(S).FATHER(N) 2.47694 (0.346868)
SON(S).FATHER(U) 2.74442 (0.631953)
SON(I).FATHER(S) 2.93119 (0.438884)
SON(I).FATHER(I) 4.13517 (0.494975)
SON(I).FATHER(N) 4.41388 (0.470993)
SON(I).FATHER(U) 5.01064 (0.701586)
SON(N).FATHER(S) 2.7264 (0.343167)
SON(N).FATHER(I) 4.03093 (0.41346)
SON(N).FATHER(N) 4.95348 (0.385207)
SON(N).FATHER(U) 5.69136 (0.641883)
SON(U).FATHER(S) 2.50771 (0.445978)
SON(U).FATHER(I) 3.99903 (0.496312)
SON(U).FATHER(N) 5.29608 (0.467617)
SON(U).FATHER(U) 6.75256 (0.693373)
Scale taken as: 1
Deviance: 3.37508e-14
Number of cases: 25
Degrees of freedom: 0
Anthony Rossini