- I'll not have an office hour after class today -- sorry!
- Exam 1 Key (missing one page yet)
I'm going to scan them again -- I don't like the quality
- Section 8.6 homework:
- #31 - two integrations by parts
- #84 - don't be scared of ugly constants!
- 9.1 homework due tomorrow.
- Examples:
- #19, p. 500 (Maclaurin series polynomial)
- #23, p. 500 (Taylor series polynomial)
- #35, p. 500 (Let's do sin(x) as well (Maclaurin series polynomial))
- #46, p. 501
- We'll just get started today. We've just studied Taylor series,
and we might recognize the following image:
What would we get if we could add up all these (infinite!) terms? 148.4131591025766...
- Definition: A sequence is a function f(n) whose
domain is a subset of the integers. The values
are called the terms of the sequence and n is called the index.
- In the example sequence above, what do you suppose is the limit of
the sequence as
?
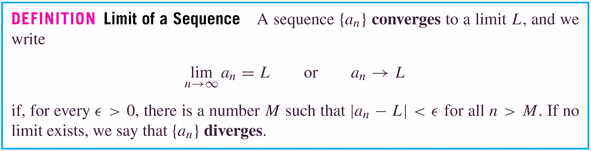
-

-
